Chapter3 - Counting 101 - Recursion and Recurrence(2)

Book - Python Algorithms by Magnus Lie Hetland

Chapter 3 - Counting 101

Guessing and Checking

Inductive Proof (귀납적 증명)

Unraveling recurrence and finding a pattern is subject to unwarranted assumption. To be sure that a solution is correct, we should conjure up a solution by guess work or intuition and then show that it’s right.
For example, take \(T(n) = T(n-1) + 1\).
We want to check whether \(T(n)\) is \(O(n)\).
To find this, we try to verify that \(T(n) ≤ cn\), for some an arbitrary \(c ≥ 1\).
We set \(T(1) = 1\). And it’s right.

How about large values for n?
This is where the induction comes in. The idea is quite simple: We start with \(T(1)\), where we know our solution is correct, and then we try to show that it also applies to \(T(2)\), \(T(3)\), and so forth.
By proving an induction step, showing that if our solution is correct for \(T(n–1)\), it will also be true for \(T(n)\), for \(n > 1\). This step would let us go from \(T(1)\) to \(T(2)\), from \(T(2)\) to \(T(3)\), and so forth, just like we want.

\(T(n–1) ≤ c(n–1)\) leads to \(T(n) ≤ cn\), which (consequently) leads to \(T(n+1) ≤ c(n+1)\), and so forth. Starting at our base case, \(T(1)\), we have now shown that \(T(n)\) is, in general, \(O(n)\).

Strong Induction

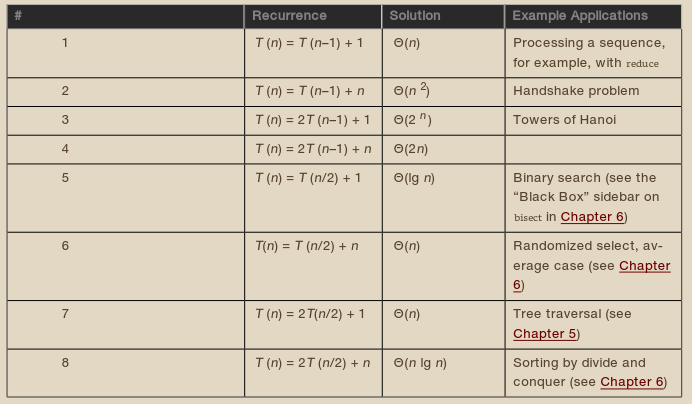
Let’s do recurrence 8 from [table 3-1]. Now, an induction hypothesis will be about all smaller numbers. More specifically, I’ll assume that \(T(k) ≤ ck \log k\) for all positive integers \(k < n\) and show that this leads to \(T(n) ≤ cn \log n\). In particular, we now hypothesize something about \(T(n/2)\) as well, not just \(T(n–1)\).

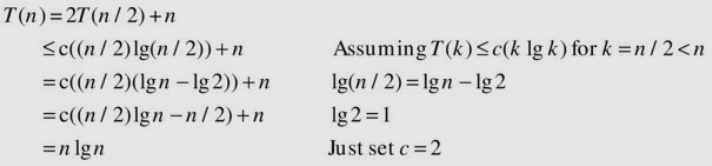
[Table 3-1]