ML basics - Linear Models for Regression
선형 기저 함수 모델
가장 단순한 형태의 선형모델
\[y(\boldsymbol{x}, \boldsymbol{w}) = w_{0}+w_{1}x_{1}+\cdots w_{D}x_{D}\] \[\boldsymbol{x} = (x_{1},\cdots,x_{D})^{T}\]이 모델의 파라미터는 \(\boldsymbol{w} = (w_{0},\cdots,w_{D})^{T}\) 벡터이다. 위 함수는 파라미터 \(\boldsymbol{w}\)에 대해 선형일 뿐만 아니라 입력 데이터 \(\boldsymbol{x}\)에 대해서도 선형이다.
\(\boldsymbol{x}\)에 대해 비선형인 함수를 만들고 싶다면?
\[y(\boldsymbol{x}, \boldsymbol{w}) = w_{0}+\sum_{j=1}^{M-1}w_{j}\phi_{j}(\boldsymbol{x})\]\[y(\boldsymbol{x}, \boldsymbol{w}) = \sum_{j=0}^{M-1}w_{j}\phi_{j}(\boldsymbol{x}) = \boldsymbol{w}^{T}\phi(\boldsymbol{x})\] \[\phi_{0}(\boldsymbol{x}) = 1\]편의상 \(w_{0}\)를 따로 쓰지 않고, \(\phi_{0}(\boldsymbol{x}) = 1\)로 정의를 하면 아래와 같이 간단하게 나타낼 수 있다.
\(\boldsymbol{x}\) 에 대해 비선형인 함수 \(\phi_{j}(\boldsymbol{x})\) 를 기저함수(basis function)라고 부른다.
\(\phi_{j}(\boldsymbol{x})\)는 \(\boldsymbol{x}\)에 대해서는 비선형이지만, 여전히 \(\boldsymbol{w}\)에 대해서는 선형함수이다.
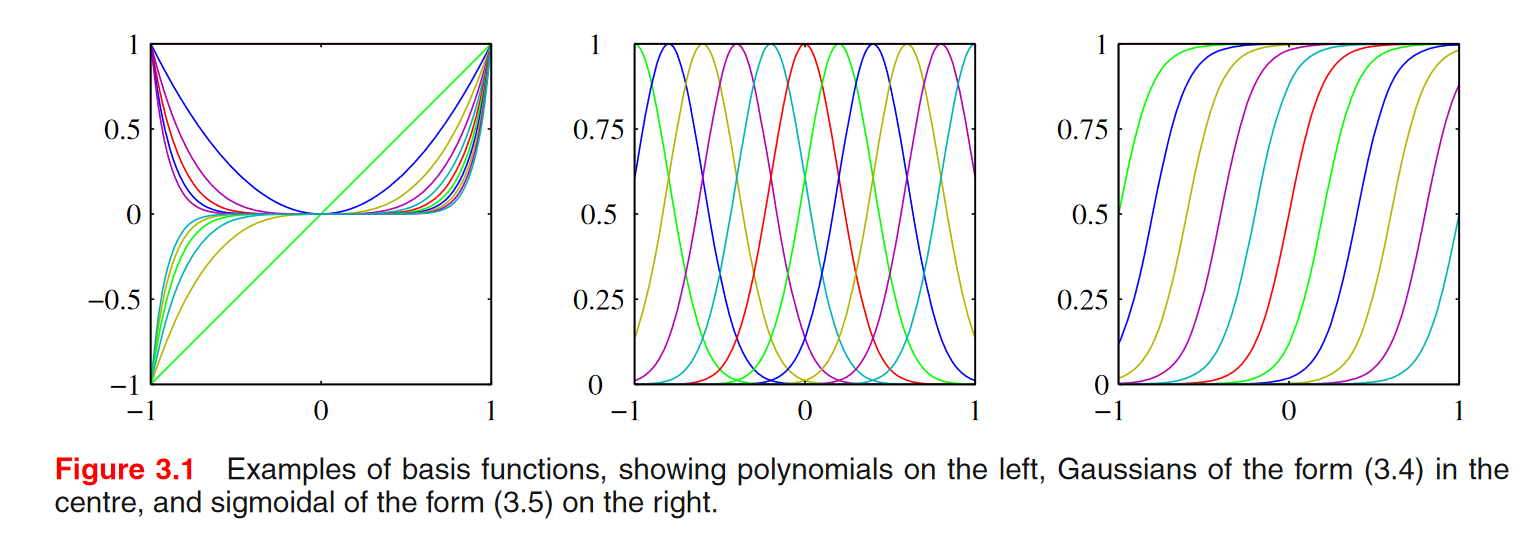
앞에서 몇 가지 기저함수를 이미 사용한 적이 있다.
- 다항식 기저함수
- 가우시안 기저함수
\(\mu_{j}\): 그래프의 위치를 결정하는 parameter, \(s\)는 얼마나 옆으로 퍼지는 지.
- 시그모이드 기저함수
시그모이드에서도 \(\mu_{j}\)와 \(s\)는 위치와 옆으로 퍼진 정도를 결정한다.
\(\sum_{j=1}^{M-1}w_{j}\phi_{j}(\boldsymbol{x})\)여기에서 \(\boldsymbol{x}\)가 벡터, 반드시 \(\phi\)함수가 하나의 scalar값일 필요는 없고 벡터를 input으로 받아서 scalar 값을 되돌려줘도 된다는 점.
예를 들어, \(x = (x_1, x_2)^T\)일때, \(\phi_1(x_1,x_2) = x_1^2\), \(\phi_2(x_1,x_2) = x_2^2\), \(\phi_3(x_1,x_2) = x_1 x_2\) 이런식으로 나타낼 수 있다.따라서 기저함수 안에 들어가는 \(\boldsymbol{x}\)는 원래 input \(\boldsymbol{x}\) 전체가 될 수 있음.
최대우도와 최소제곱법 (Maximum Likelihood and Least Squares)
에러함수가 가우시안 노이즈를 가정할 때 최대우도로부터 유도될 수 있다는 것을 살펴본 적이 있다. 조금 더 자세히 살펴보자.
\[t = y(\boldsymbol{x}, \boldsymbol{w}) + \epsilon\]- \(y(\boldsymbol{x}, \boldsymbol{w})\) 는 결정론적 함수(deterministic)
- \(\epsilon\)는 가우시안 분포 \(\mathcal{N}(\epsilon\vert 0, \beta^{-1})\)를 따르는 노이즈 확률변수
deterministic한 함수에 가우시안 분포를 따르는 확률변수를 더했기 때문에, 목표값인 변수 \(t\)도 가우시안 분포를 따른다.
따라서 \(t\) 의 분포는 다음과 같다.
\[p(t\vert \boldsymbol{x}, \boldsymbol{w}, \beta) = \mathcal{N}(t\vert y(\boldsymbol{x}, \boldsymbol{w}), \beta^{-1})\]평균이 \(y(\boldsymbol{x}, \boldsymbol{w})\), 분산 또는 정확도는 \(\beta^{-1}\)이 노이즈 값과 같게 된다.
제곱합이 손실함수로 쓰이는 경우(squared loss function), 새로운 \(\boldsymbol{x}\) 가 주어졌을 때 \(t\) 의 최적의 예측값(optimal prediction)은 \(t\) 의 조건부 기댓값이다.
\(t\) 가 위의 분포를 따르는 경우 조건부 기댓값은 다음과 같다.
\[\mathbb{E}[t\vert \boldsymbol{x}] = \int tp(t\vert \boldsymbol{x})dt = y(\boldsymbol{x}, \boldsymbol{w})\]결정이론에서 optimal prediction는 조건부 기댓값임을 배웠다.
https://marquis08.github.io/devcourse2/decisiontheory/linearregression/mathjax/ML-basics-DecisionTheory-LinearRegression/#regression
우리가 할 수 있는 건 \(\boldsymbol{w}\)의 최적의 값을 찾아서, 새로운 \(\boldsymbol{x}\)가 들어올 때 \(y(\boldsymbol{x}, \boldsymbol{w})\) 이 함수값을 계산해서 예측하는 것이 최선이다.
ML
이제 파라미터인 \(\boldsymbol{w}\) 를 찾기 위해 최대우도 추정법을 사용해보자.
- 입력값 \(\boldsymbol{X} = \boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{N}\)
- 출력값은 \(\boldsymbol{t} = \boldsymbol{t}_{1},\cdots,\boldsymbol{t}_{N}\)
Supervised learning 문제에서는 입력벡터를 모델링하는 것이 아니라, 출력값인 \(\boldsymbol{t}\)를 모델링하기 때문에, 우도는 출력값으로 표현함.
이전에 likelihood를 표현할 때는 input값인 \(\boldsymbol{x}\)에 대해서 표현을 했지만, Supervised learning 에서는 target 값에 관한 확률을 계산해야 한다.
입력값 \(\boldsymbol{x}\)는 조건부에 나타난다는 것을 기억해야함. 하지만, \(\boldsymbol{x}\)를 조건부에서 생략하는 경우도 있다. 문맥상 명확한 경우에는 생략하기도 하니 유의할 것.
우도함수는
\[p(\boldsymbol{t}\vert \boldsymbol{X}, \boldsymbol{w}, \beta) = \prod_{n=1}^{N}\mathcal{N}(t_{n}\vert \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}), \beta^{-1})\]출력값 \(\boldsymbol{t}\)에 대해서 확률을 계산하게 되면, N개의 t가 독립적이기 때문에, N개의 가우시안 분포를 곱해주게 된다. 그리고 로그를 씌우게 되면 아래의 식이 된다.
로그 우도함수는
\[\ln p(\boldsymbol{t}\vert \boldsymbol{w}, \beta) = \sum_{n=1}^{N}\ln \mathcal{N}(t_{n}\vert \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}), \beta^{-1}) = \frac{N}{2}\ln \beta - \frac{N}{2}\ln(2\pi) - \beta\boldsymbol{E}_{D}(\boldsymbol{w})\]\[\boldsymbol{E}_{D}(\boldsymbol{w}) = \frac{1}{2}\sum_{n=1}^{N}\{ t_{n}- \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}) \}^{2}\]\(\boldsymbol{w}\)와 관련된 부분은 마지막 항이다.
따라서, 로그 우도함수를 최대화시키는 \(\boldsymbol{w}\) 값은 \(\boldsymbol{E}_{D}(\boldsymbol{w})\) 로 주어진 제곱합 에러함수를 최소화시키는 값과 동일하다는 것을 알 수 있음.
우도를 최대화 시키는 \(\boldsymbol{w}\)를 찾기 위해서는 우도를 \(\boldsymbol{w}\)에 관해서 미분을 하고, 그것을 0으로 놓고, \(\boldsymbol{w}\)에 관해서 풀면 됨.
\(\boldsymbol{w}\) 에 대한 기울기벡터(gradient vector)는
\[\nabla\ln p(\boldsymbol{t}\vert \boldsymbol{w}, \beta) = \sum_{n=1}^{N}\{ \boldsymbol{t}_{n} - \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}) \}\phi(\boldsymbol{x}_{n})^{T}\]\(\boldsymbol{w}\)에 관해서 로그우도를 미분하면 아래와 같은 식이 나온다.
따라서 \(\boldsymbol{w}\) 의 최적값은
\[\boldsymbol{w}_{ML} = (\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t}\]위의 미분한식을 0으로 놓고 풀게 되면, 아래의 식이 나오게 됨
위 식을 normal equations라고 부른다.
\[\Phi = \begin{pmatrix} \phi_{0}(\boldsymbol{x}_{1}) & \phi_{1}(\boldsymbol{x}_{1}) & \ldots & \phi_{M-1}(\boldsymbol{x}_{1}) \cr \phi_{0}(\boldsymbol{x}_{2}) & \phi_{1}(\boldsymbol{x}_{2}) &\ldots & \phi_{M-1}(\boldsymbol{x}_{2}) \cr \vdots & \vdots & \ddots & \vdots \cr \phi_{0}(\boldsymbol{x}_{N}) & \phi_{1}(\boldsymbol{x}_{N}) & \ldots & \phi_{M-1}(\boldsymbol{x}_{N}) \end{pmatrix}\]N개의 행과 M개의열이 있다. 각각의 행은 하나의 data point를 의미, 각각의 데이터는 M개의 기저함수를 가지게 된다. 기저함수를 통해서 M개의 element가 생성됨.
이런 행렬 \(\phi\)를 design matrix라고 부른다.
Moore-Penrose pseudo-inverse
\[\Phi^{\dagger} \equiv (\Phi^{T}\Phi)^{-1}\Phi^{T}\]\(\Phi\boldsymbol{w}\approx \boldsymbol{t}\)와 가장 가깝게 되기를 원한다고 했을 때, \(\Phi\)가 square matrix였다면 역행렬을 양쪽에 곱하면 되겠지만 그렇지 않을 경우에 많기 때문에 역행렬은 존재불가하다고 보면되고, 대신에 최대한 비슷한 값을 가지도록하는 \(\boldsymbol{w}\)를 찾는다고 했을 때, 역행렬과 유사한 방식으로 \(\boldsymbol{w}\approx (\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t}\) 이러한 형태를 만들 수 있기 때문에 pseudo-inverse라고 부르는 이유다.
Normal Equation 유도하기
\[\Phi\boldsymbol{w}\approx \boldsymbol{t}\]norm을 생각해보자.
앞에 어떤 상수를 곱해도 최소값은 그대로 일 것이기 때문에 상수 1/2를 붙임.
맨 마지막 항인 \(\boldsymbol{t}^{T}\boldsymbol{t}\)는 w와 상관없기 때문에 지우고, \(- \boldsymbol{t}^{T}\Phi\boldsymbol{w} - \boldsymbol{w}^{T}\Phi^{T}\boldsymbol{t}\)이 부분은 같기 때문에 1/2을 곱해주면 \(- \boldsymbol{t}^{T}\Phi\boldsymbol{w}\)만 남게 됨.
이식을 \(\boldsymbol{E}(\boldsymbol{w})\)라는 error함수라고 하고, w에 관해서 미분함.
\(\frac{1}{2}\boldsymbol{w}^{T}\Phi^{T}\Phi\boldsymbol{w} - \boldsymbol{t}^{T}\Phi\boldsymbol{w}\) 이 식을 미분하는데, 선형대수에서 배운 공식 중에서 \(\nabla_x x^TAx = 2Ax\)를 활용하면 됨. 즉, x에 관해서 미분할 때 이러한 이차형식 형태로 주어지면 2Ax로 gradient를 구하는게 가능하다.
행렬미분의 중요한 공식들: http://127.0.0.1:4000/devcourse2/linearalgebra/mathjax/ML-basics-Linear-Algebra/#%EC%A4%91%EC%9A%94%ED%95%9C-%EA%B3%B5%EC%8B%9D%EB%93%A4따라서 \(\frac{1}{2}\boldsymbol{w}^{T}\Phi^{T}\Phi\boldsymbol{w} = \Phi^{T}\Phi\boldsymbol{w}\)가 됨.
\(\boldsymbol{t}^{T}\Phi\boldsymbol{w}\) 이 부분은 transpose를 하면 됨.
따라서,
\[\nabla_{w}\boldsymbol{E}(\boldsymbol{w}) = \Phi^{T}\Phi\boldsymbol{w} - \Phi^{T}\boldsymbol{t}\]\[\begin{align}\Phi^{T}\Phi\boldsymbol{w} &= \Phi^{T}\boldsymbol{t} \\ \boldsymbol{w} &= (\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t} \end{align}\]이 값을 0으로 놓고 풀면 됨.
\(\Phi^{T}\Phi\) 이 square matrix 이기 때문에 역행렬이 존재한다면, 이를 넘겨주면 됨.
결과적으로 이것이
\[\boldsymbol{w}_{ML} = (\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t}\]하지만 모든 경우에 \(\Phi^{T}\Phi\) 이 square matrix의 역행렬이 존재하는 것은 아님. 하나의 조건을 만족하면 되는데, Design Matrix(\(\Phi\))의 모든 열들이 선형 독립이기만 하다면 가능함.
ML - 편향 파라미터 (bias parameter) \(\boldsymbol{w}_{0}\)
\[\boldsymbol{E}_{D}(\boldsymbol{w}) = \frac{1}{2}\sum_{n=1}^{N}\{ \boldsymbol{t}_{n} - \boldsymbol{w}_{0}-\sum_{j=1}^{M-1}\boldsymbol{w}_{j}\phi_{j}(\boldsymbol{x}_{n}) \}^{2}\] \[\boldsymbol{w}_{0} = \bar t - \sum_{j=1}^{M-1}\boldsymbol{w}_{j}\bar{\phi_{j}}\] \[\bar t = \frac{1}{N}\sum_{n=1}^{N}t_{n},\ \bar{\phi_{j}} = \frac{1}{N}\sum_{n=1}^{N}\phi(\boldsymbol{x}_{n})\]파라미터 중에 \(\boldsymbol{w}_{0}\)를 명시적으로 구분을 해놓고 \(\boldsymbol{w}_{0}\)에 대해서 최대 우도해를 구함.
\(\bar t\): target 값의 평균, \(\bar{\phi_{j}}\): 하나의 기저함수를 N개의 데이터에 대해 평균을 낸 값.
\(\boldsymbol{w}_{0}\)은 target 값의 평균과 \(\sum_{j=1}^{M-1}\boldsymbol{w}_{j}\bar{\phi_{j}}\) 사이의 차이를 보정하는 역할
ML - \(\beta\)(precision)
\[\frac{1}{\beta_{ML}} = \frac{1}{N}\sum_{n=1}^{N}{\boldsymbol{t}_{n} - \boldsymbol{w}_{ML}^{T}\phi(\boldsymbol{x}_{n})}^{2}\]미분을 해서 푼 값이 아래와 같다.
목표값이 분산되어 있는 정도
기하학적 의미
- 벡터의 집합 (\(\{ \boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{n} \}\)) 에 대한 생성(span)
- 행렬의 치역(range)
행렬 \(\boldsymbol{A} \in \mathbb{R}^{m\times n}\) 의 치역 \(\mathcal{R}(\boldsymbol{A})\) 는 \(\boldsymbol{A}\) 의 모든 열들에 대한 생성(span)이다.
- 벡터의 사영(projection)
벡터 \(\boldsymbol{t} \in \mathbb{R}^{m}\) 의 \(span(\{ \boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{n} \})(\boldsymbol{x}_{i}\in \mathcal{R}^{m})\) 으로의 사영은 \(span(\{ \boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{n} \})\) 에 속한 벡터 중 \(\boldsymbol{t}\) 에 가장 가까운 벡터로 정의된다.
\[Proj(\boldsymbol{t}; \{ \boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{n} \}) = \arg\min\ _{v\in span(\{ \boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{n} \})}\Vert\boldsymbol{t}-\boldsymbol{v} \Vert_{2}\]Span이 주어지는 것이 아니라, 행렬이 주어질 경우에, span 대신에 행렬의 치역으로 Projection한다.
\(Proj(\boldsymbol{t};\boldsymbol{A})\) 은 행렬 \(\boldsymbol{A}\) 의 치역으로의 사영이다. \(\boldsymbol{A}\) 의 열들이 선형독립이면,
\[Proj(\boldsymbol{t};\boldsymbol{A}) = \arg\min\ _{v\in \mathcal{R}(\boldsymbol{A})}\Vert\boldsymbol{t}-\boldsymbol{v} \Vert_{2} = \boldsymbol{A}(\boldsymbol{A}^{T}\boldsymbol{A})^{-1}\boldsymbol{A}^{T}\boldsymbol{t}\]\(A\)대신에 \(\Phi\)를 사용하면, \(\Phi(\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t} = \boldsymbol{w}_{ML}\)의 형태가 나타난 것을 볼 수 있음.
결국 \(\Phi\)가 주어졌을 때, 목표값 벡터에 가장 가깝게 갈 수 있는 벡터를 구한 것이 됨.
span 대신에 design matrix \(\Phi\)에 대해서 수직으로 내렸을 때 \(y\)가 되는데 이 \(y\)를 구하기 위한 공식이 \(\Phi(\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t}\) 이 것임.
\(\boldsymbol{w}_{ML}\)와 \(\Phi(\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t}\)를 곱합 것이 이 그림에서 \(y\)를 표현한 것.

온라인 학습 (Sequantial Learning)
배치학습 vs. 온라인 학습
Stochastic gradient decent
에러함수가 \(\boldsymbol{E} = \sum_{n}\boldsymbol{E}_{n}\) 이라고 하자.
\[\boldsymbol{w}^{\tau+1}=\boldsymbol{w}^{\tau} - \eta\nabla\boldsymbol{E}_{n}\]에러 함수를 각각의 샘플에 대한 에러들의 합으로 표현 함.
제곱합 에러를 사용한다면, \(\boldsymbol{E} = \frac{1}{2}\sum_{n=1}^{N}( \boldsymbol{t}_{n} - \boldsymbol{w}^{T}\phi_{n} )^2\)
여기서 \(\phi_{n} = \phi(\boldsymbol{x}_{n})\) 이고 \(\boldsymbol{x}_{n}\)이 주어졌을 때 기저함수의 output값이다.
\[\boldsymbol{E}_{n} = \frac{1}{2}( \boldsymbol{t}_{n} - \boldsymbol{w}^{T}\phi_{n} )^2\]일반적인 Gradient의 경우에는 파라미터를 업데이트 할 때, \(\boldsymbol{E}_{n}\)이 아니라 에러함수 전체에 대해서 함.
SGD 같은 경우 하나의 n 값에 대해서 함.
gradient를 구하면, \(\nabla\boldsymbol{E}_{n} = (\boldsymbol{t}_{n} - \boldsymbol{w}^{T}\phi_{n})(- \phi_{n})\) 되고 이것을 아래의 식에 넣으면 업데이트 룰이 완성됨.
제곱합 에러함수인 경우
\[\boldsymbol{w}^{\tau+1}=\boldsymbol{w}^{\tau} + \eta(t_{n}-\boldsymbol{w}^{\tau}T\phi_{n})\phi_{n}\] \[\phi_{n} = \phi(\boldsymbol{x}_{n})\]데이터가 많더라도 하나의 샘플씩 보기 때문에 시간은 걸리지만 메모리 부담은 줄어들 것.
실습 (대규모의 선형회귀)
normal equations를 구할때,
\[(\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t}\] \[\Phi^{T} = \begin{bmatrix} \vert &\ \\ \phi(x_{1}) & \ldots \\ \vert &\ \end{bmatrix}\ \Phi = \begin{bmatrix} - & \phi(x_{1})^{T} & - \\ \ & \vdots & \ \end{bmatrix}\] \[\Phi^{T}\Phi = \sum_{n=1}^{N}\phi(x_{n})\phi(x_{n})^{T}\]행벡터와 열벡터를 곱하면 합의 형태로 나온다. \(\phi(x_{n})\phi(x_{n})^{T}\)이 outer product 이기 때문에 행렬이고, 이 행렬의 값을 N번만큼 더한 것임.
\[\Phi^{T}\boldsymbol{t}\]이 사실을 활용하면, 굳이 데이터를 한꺼번에 읽지 않더라도 각각의 데이터를 읽어서 자신과의 outer product값을 구하고 저장하고 그 값들을 더하면 되는 것임.
이 부분도 비슷하게, 앞부분이 열벡터이고 \(\boldsymbol{t}\)도 하나의 벡터이기 때문에, \(\boldsymbol{t}\)의 각각의 element들이 계수가 되어서 열벡터들에 곱해지고 그것들을 더하면 됨.
알고리즘화를 시켜보면,
0으로 초기화한 (M x M) 사이즈의 A라는 행렬을 선언함.
0으로 초기화한 (M x 1) 사이즈의 b라는 행렬을 선언함.
for i in range(1 , N+1): A = A + \(\phi(x_{i})\phi(x_{i})^{T}\) (외적) b = b + \(\phi(x_{i})\boldsymbol{t}_{i}\) (곱)
iteration이 끝난 후,
\[A = \Phi^{T}\Phi, b = \Phi^{T}\boldsymbol{t}\] \[W = A^{-1}b\]규제화된 최소제곱법 (Regularized Least Squares)
\(\boldsymbol{E}_{D}(\boldsymbol{w}) + \lambda\boldsymbol{E}_{w}(\boldsymbol{w})\)
규제화 항 \(\lambda\boldsymbol{E}_{w}(\boldsymbol{w})\)은 \(\boldsymbol{w}\)의 norm 값에 파라미터 \(\lambda\)를 곱한 값으로 나타낼 수 있음.
\(\lambda\)로 규제화를 조정.
가장 단순한 형태는
\[\boldsymbol{E}_{w}(\boldsymbol{w}) = \frac{1}{2}\boldsymbol{w}^{T}\boldsymbol{w}\] \[\boldsymbol{E}_{D}(\boldsymbol{w}) = \frac{1}{2}\sum_{n=1}^{N}\{ t_{n} - \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}) \}^2\]최종적인 에러함수는
\[\frac{1}{2}\sum_{n=1}^{N}\{ t_{n} - \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}) \}^2 + \frac{\lambda}{2}\boldsymbol{w}^{T}\boldsymbol{w}\]간단한 형태의 규제화 항이 추가된 경우에 동일하게 Maximum Likelihood Solution을 구할 수 있음.
위의 에러 함수에 대해 \(\boldsymbol{w}\)에 대해 미분을 하고, 그것을 0으로 놓고 풀게 되면, 아래의 식이 나오게 됨.
\(\boldsymbol{w}\) 의 최적값은
\[\boldsymbol{w}^{T} = (\lambda\boldsymbol{I}+\phi^{T}\phi)^{-1}\phi^{T}\boldsymbol{t}\]앞에서 나온 ML 식과 유사하게 나온다.
일반화된 규제화
\[\boldsymbol{E}(\boldsymbol{w}) = \frac{1}{2}\sum_{n=1}^{N}\{ t_{n} - \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}) \}^2 + \frac{1}{2}\sum_{j=1}^{M}\vert\boldsymbol{w}_{j} \vert^{q}\]규제화 항을 l2가 아닌 lq norm으로 할 수도 있음.
Lasso 모델(\(q=1\))
규제화된 에러함수를 최소화 시키려고 할 때, optimization 문제를 constrained optimization 문제로 바꿔서 생각할 수 있음.
\(\frac{1}{2}\sum_{j=1}^{M}\vert\boldsymbol{w}_{j} \vert^{q}\)을 라그랑지안이라고 생각하면, 이 부분을 \(\sum_{j=1}^{M}\vert\boldsymbol{w}_{j} \vert^{q} \leq\eta\) 이러한 부등식을 만족시키는 제약조건으로 생각할 수 있음.
이러한 제약조건을 만족하면서, 제약이 없는 앞의 항 \(\frac{1}{2}\sum_{n=1}^{N}\{ t_{n} - \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}) \}^2\) 을 최소화시키는 해를 찾는 문제로 전환시켜 생각할 수 있음.
- Constrained minimization 문제로 나타낼 수 있다.
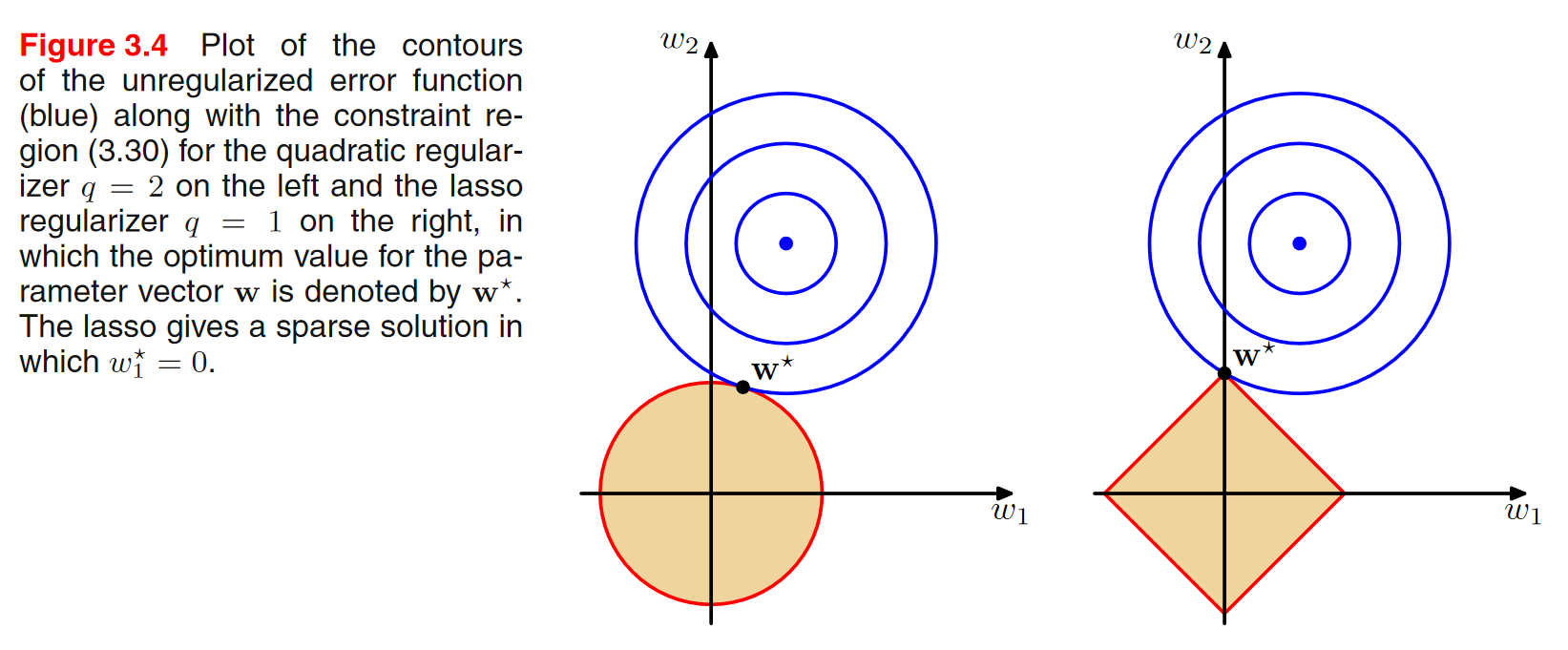
\(w_{1}\), \(w_{2}\) 2개의 parameter만 있다고 가정.
파란 contour 위에 있는 \(w_{1}\), \(w_{2}\) 점들은, 동일한 에러함수 값을 가진다는 의미. 규제화가 없는 부분을 보여주고 있음.
중간에 파란 점으로 갈 수 록 에러가 줄어든다고 보면 됨. 제약조건이 없다면 최적해는 파란점이 될텐데, 제약조건을 만족시키려면 \(w_{1}\), \(w_{2}\) 값이 칠해진 영역에 내에 있어야 함.
따라서, constraint region과 contour가 만나는 부분이 제약조건을 만족시키면서 에러가 최소화되는 최적의 해가 발생하는 지점이다.
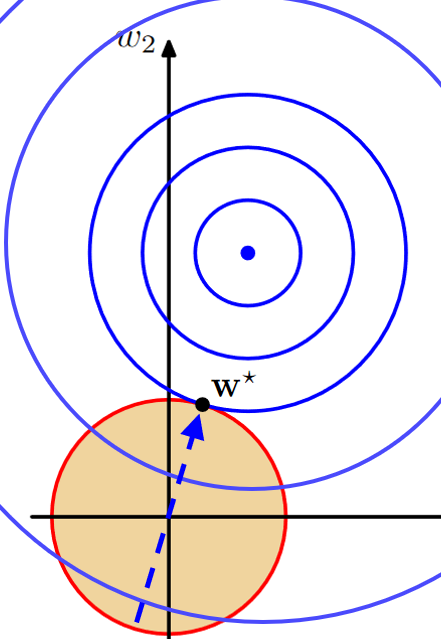
위의 그림처럼 에러지점이 최소인 곳을 향해서 가지만 제약조건 안에 있어야 한다는 것임.
l1의 경우 사각형의 꼭지점이 최소화 지점인데, 이것이 의미하는 것은 어떤 \(w\)의 값이 0이 된다는 의미 이다. Figure 3.4에서 l1의 경우는 \(w_{1}\)의 값이 0이 되는 지점이 최소화가 되는 지점인 것이다.
l1 norm을 사용하는 경우, sparse 한 모델이 얻어지게 됨. sparse하다는 의미는 파라미터들 중에 여러개의 값이 0이 됨.
편향-분산 분해(Bias-Variance Decomposition)
모델이 과적합되는 현상에 대한 이론적인 분석
제곱합 손실함수가 주어졌을 때의 최적 예측값
\[h(\boldsymbol{x}) = \mathbb{E}[t\vert \boldsymbol{x}] = \int tp(t\vert \boldsymbol{x})dt\]손실함수의 기댓값
\[\mathbb{E}[\boldsymbol{L}] = \int \{y(\boldsymbol{x}) - h(\boldsymbol{x}) \}^2p(\boldsymbol{x})d\boldsymbol{x} + \int\int \{ h(\boldsymbol{x}-t) \}^2p(\boldsymbol{x},t)d\boldsymbol{x}dt\]뒷 항인 \(\int\int \{ h(\boldsymbol{x}-t) \}^2p(\boldsymbol{x},t)d\boldsymbol{x}dt\) 이 부분은 inherent noise라고 볼 수 있음, 따라서 앞부분인 손실함수의 기댓값을 최소화하기 위한 노력을 하는 것임.
제한된 데이터셋 \(D\) 만 주어져 있기 때문에 \(h(\boldsymbol{x})\) 를 정확히 알 수 는 없다. 대신 파라미터화 된 함수 \(y(\boldsymbol{x}, \boldsymbol{w})\) 를 사용해 최대한 손실함수의 기댓값을 최소화하고자 한다.
제한된 데이터로 인해 발생하는 모델의 불확실성을 어떻게든 표현해야 한다.
- 베이지안 방법: 모델 파라미터 \(\boldsymbol{w}\) 의 사후확률분포를 계산한다.
- 빈도주의 방법: 모델 파라미터 \(\boldsymbol{w}\) 의 점추정 값을 구하고 여러 개의 데이터셋을 가정했을 때 발생하는 평균적인 손실을 계산하는 ‘가상의 실험’을 통해 점추정 값의 불확실성을 해석한다.
특정 데이터셋 \(D\) 에 대한 손실을
\[\boldsymbol{L}(\mathcal{D}) = \{y(\boldsymbol{x};\mathcal{D})-h(\boldsymbol{x}) \}^2\]라고 하자. 손실함수의 기댓값은
\[\mathbb{E}[\boldsymbol{L}(\mathcal{D})] = \int \{y(\boldsymbol{x};\mathcal{D})-h(\boldsymbol{x})\}^2 p(\boldsymbol{x})d\boldsymbol{x} + noise\]여러 개의 데이터셋 \(\mathcal{D}_{1},\cdots,\mathcal{D}_{L}\) 이 주어졌을 때 이 값들의 평균을 생각해보자.
\[\frac{1}{\boldsymbol{L}}\sum_{l=1}^{L} \left[ \int \{y(\boldsymbol{x};\mathcal{D}^{(i)})-h(\boldsymbol{x})\}^2 p(\boldsymbol{x})d\boldsymbol{x} + noise \right] = \int \mathbb{E}_{\mathcal{D}} \left[ \{y(\boldsymbol{x};\mathcal{D})-h(\boldsymbol{x}) \}^2 \right] p(\boldsymbol{x})d\boldsymbol{x} + noise\]\[\begin{align}&\ \{y(\boldsymbol{x};\mathcal{D}) -\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right] +\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right] -h(\boldsymbol{x}) \}^2 \\ &= \{y(\boldsymbol{x};\mathcal{D}) -\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right]\}^2 + \{\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right] - h(\boldsymbol{x})\}^2 + 2\{y(\boldsymbol{x};\mathcal{D}) -\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right]\}\{\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right] - h(\boldsymbol{x})\} \end{align}\]합 부분에 적분안으로 들어간다고 생각하면, \(\mathbb{E}_{\mathcal{D}}\), 즉 \(\mathcal{D}\)에 관한 기댓값으로 생각할 수 있음.
기댓값 안에 있는 제곱부분에 대해서 먼저 생각해보자.
\(\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right]\)( D가 주어졌을때 y함수의 \(\mathcal{D}\)에 관한 기댓값 ) 이 것을 더하고 빼는 연산을 추가함.
교차항인 \(2\{y(\boldsymbol{x};\mathcal{D}) -\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right]\}\{\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right] - h(\boldsymbol{x})\}\)은 사라지게 됨.
\(\{\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right] - h(\boldsymbol{x})\}^2\) 이 부분은 \(\mathcal{D}\)에 관한 함수가 아니기 때문에(\(\mathcal{D}\)에 관해서 기댓값을 구하고 되면 그 뒤에는 더이상 \(\mathcal{D}\)에 관한 함수가 아닌게 되버림) \(\{\mathbb{E}_{\mathcal{D}} \left[y(\boldsymbol{x};\mathcal{D})\right]-h(\boldsymbol{x})\}^2\) 이렇게 그대로 내려왔고, \(h(\boldsymbol{x})\) 역시 \(\mathcal{D}\)에 의존성이 없기 때문에 그대로.
\(\{y(\boldsymbol{x};\mathcal{D}) -\boldsymbol{E}_{\mathcal{D}}\left[y(\boldsymbol{x};\mathcal{D})\right]\}^2\) 이 부분은 기댓값을 적용하게 되면, \(\mathbb{E}_{\mathcal{D}}\left[ \{y(\boldsymbol{x};\mathcal{D}) - \mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right]\}^2 \right]\) 이런식으로 \(\mathbb{E}_{\mathcal{D}}\) 기댓값이 붙어서 내려오게 된 것임.
따라서
\[\mathbb{E}_{\mathcal{D}} \left[ \{y(\boldsymbol{x};\mathcal{D})-h(\boldsymbol{x}) \}^2 \right] = \{\mathbb{E}_{\mathcal{D}} \left[y(\boldsymbol{x};\mathcal{D})\right]-h(\boldsymbol{x})\}^2 + \mathbb{E}_{\mathcal{D}}\left[ \{y(\boldsymbol{x};\mathcal{D}) - \mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right]\}^2 \right]\]정리하자면
\[\text{Expected loss} = (\text{bias})^2 + \text{variance} + \text{noise}\]\[(\text{bias})^2 = \int \{\mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right] - h(\boldsymbol{x}) \}^2 p(\boldsymbol{x})d\boldsymbol{x}\]noise는 inherent하기 때문에, 결국 Expected loss는 편향과 분산의 합으로 결정됨.
\[\text{variance} = \int \mathbb{E}_{\mathcal{D}} \left[\{ y(\boldsymbol{x};\mathcal{D}) - \mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right] \}^2\right] p(\boldsymbol{x})d\boldsymbol{x}\]\(\mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right]\) 이 부분이 평균 예측값으로 볼 수 있음. 데이터셋이 여러개 주어졌을 때 같은 x에 관한 출력값을 평균낸 것임. 따라서 평균 예측값이 \(h(\boldsymbol{x})\)로 부터 떨어져 있는 지를 보여줌.
\[\text{noise} = \int\int \{h(\boldsymbol{x})-t\}^2 p(\boldsymbol{x},t)d\boldsymbol{x}\]\(y(\boldsymbol{x};\mathcal{D}) - \mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right]\): 평균 예측값( \(\mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right]\) ) 각각의 예측값( \(y(\boldsymbol{x};\mathcal{D})\) )이 주어졌을 때의 예측값과 얼마나 떨어져 있는 지.
모델의 자유도가 높을 수록 편향 값이 낮게 나오는 경향이 있음. 모델의 자유도가 높다는 것은 모델의 복잡도가 높다는 것과 같음. linear한 모델의 경우 편향이 높은 경향을 보임.
반대로 분산의 경우 커지는 경향이 있음. 즉, 다른 데이터셋이 주어졌을 때 그 데이터셋에 대한 민감도가 높은 경향을 보임.
예제
\(h(\boldsymbol{x}) = \sin(2\pi x)\)
\[\begin{align}\bar y(x) &= \frac{1}{L}\sum_{l=1}^{L}y^{(l)}(x) \\ (\text{bias})^2 &= \frac{1}{N}\sum_{n=1}^{N}\{ \bar y(x_{n})-h(x_{n}) \}^2 \\ \text{variance} &= \frac{1}{N}\sum_{n=1}^{N}\frac{1}{L}\sum_{l=1}^{L}\{ y^{(l)}(x_{n})-\bar y(x_{n}) \}^2 \end{align}\]\(y(\boldsymbol{x};\mathcal{D}) \leftarrow y^{(l)}(x)\)
\(\mathbb{E}_{\mathcal{D}}\left[ y(\boldsymbol{x};\mathcal{D}) \right] \leftarrow \bar y(x)\)
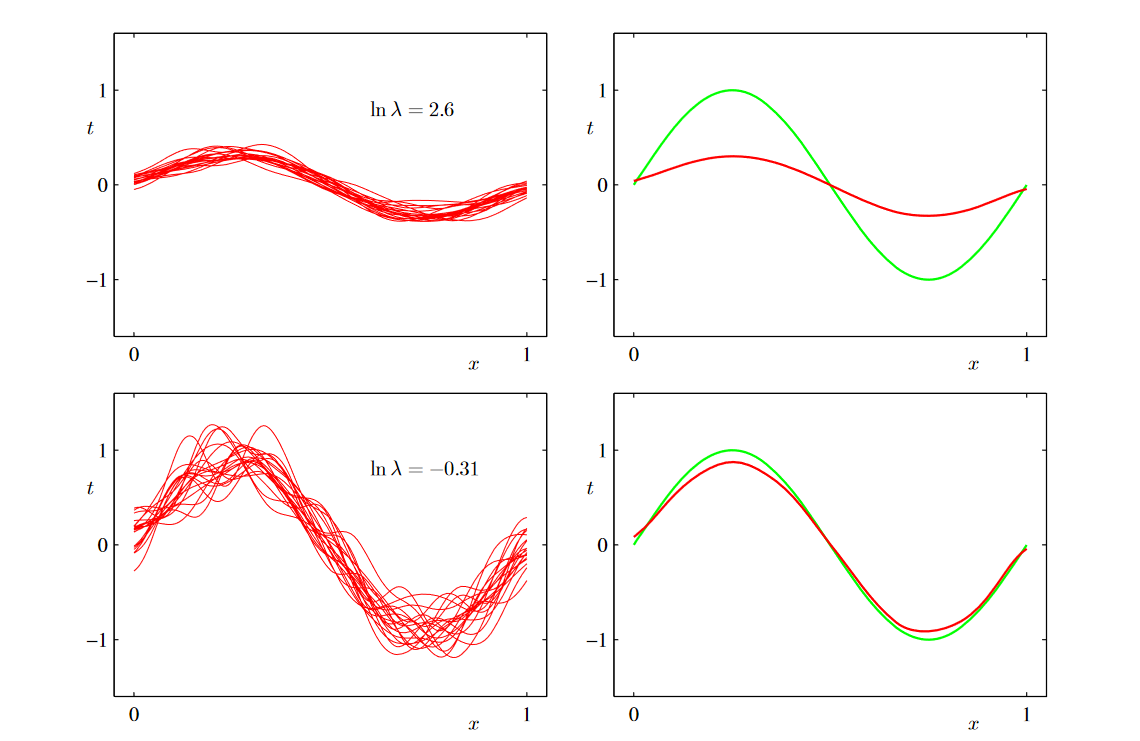
100개의 데이터셋 L, 각각의 데이터셋에 25개의 데이터가 존재한다고 가정. (L=100, N=25)
규제화와 가우시안 기저함수를 사용했을 때의 학습 결과이다. \(\lambda\) 값이 클수록 규제화가 많이 되기 때문에 모델의 자유도가 낮다. 반대로 \(\lambda\) 작을수록 규제화가 작기 때문에 모델의 자유도(복잡도)가 높다.
오른쪽 그래프에서 red line: \(\bar y(x)\), green line: \(h(\boldsymbol{x})\)
그래프에서 첫번째 행에서, \(\lambda\)가 크기 때문에 모델의 자유도가 낮은 경우, 왼쪽의 그래프를 보면, 각각의 데이터셋에 대해서 예측값들이 서로 비슷함. 이는 분산이 작음을 알 수 있음. 하지만 평균값이 h(x)로부터 많이 떨어져 있기 때문에, 편향은 큼.
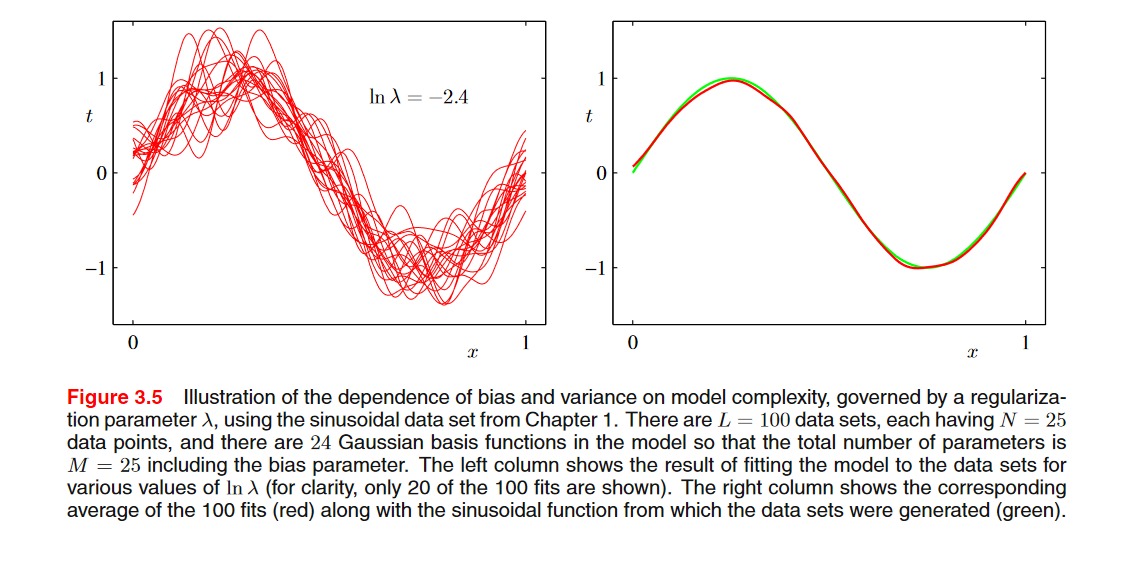
- 별개의 테스트 데이터셋에 대한 결과
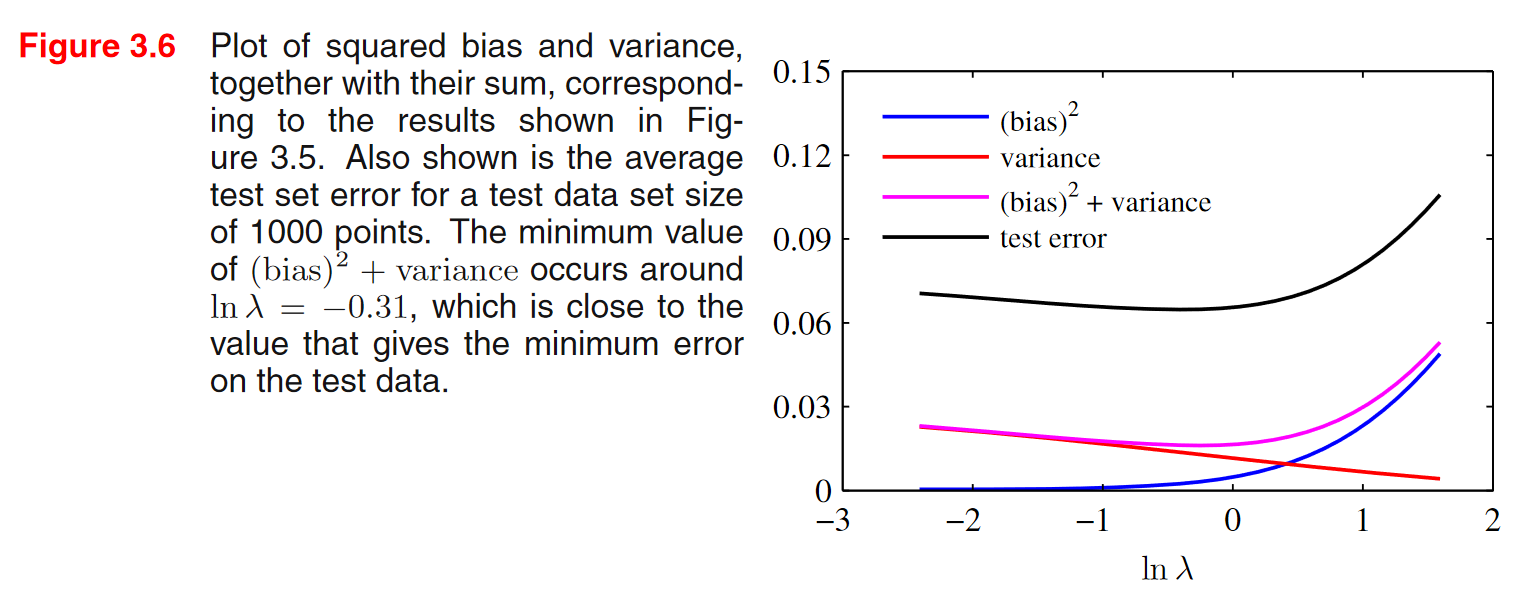
x축이 \(\lambda\)인 것을 보면, 왼쪽으로 갈 수록 자유도는 증가하고 오른쪽으로 갈 수록 자유도는 줄어듬.
\((\text{bias})^2 + \text{variance}\)가 최소인 부분과 test error가 최소인 부분이 거의 동일함을 알 수 있음.
베이지안 선형회귀 (Bayesian Linear Regression)
제한적인 데이터가 주어졌을 때, 빈도주의적 방법으로 접근하게 되면 모델의 불확실성을 나타내기가 힘든 것을 알 수 있음.
베이지안 방식을 사용하게 되면, 모델의 파라미터를 학습하면서 파라미터의 분포까지 학습을 하게 됨. 주어진 데이터가 작더라도, 학습한 모델의 불확실성을 잘 나타낼 수 있음.
- 파라미터 \(\boldsymbol{w}\) 의 사전확률을 다음과 같은 가우시안 분포라고 하자.
- 우도
선형모델의 출력값 (\(\boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n})\)) 이 평균이 됨
\[\prod_{n=1}^{N}\mathcal{N}(t_{n}\vert \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}), \beta^{-1})의 지수부 \Rightarrow -\frac{\beta}{2}\sum_{n=1}^{N}(t_{n} - \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}))^2 = \frac{\beta}{2}\Vert \boldsymbol{t} - \Phi\boldsymbol{w}\Vert_{2}^2\]\(= -\frac{\beta}{2}(\boldsymbol{t} - \Phi\boldsymbol{w})^{T}(\boldsymbol{t} - \Phi\boldsymbol{w})\) 이 부분이 지수부이기 때문에 이차형식으로 정리.
\(= -\frac{1}{2}(\boldsymbol{t} - \Phi\boldsymbol{w})^{T}(\beta\boldsymbol{I})(\boldsymbol{t} - \Phi\boldsymbol{w})\) 이렇게 이차형식으로 정리.
중간에 있는 \((\beta\boldsymbol{I})\) 이 공분산의 역행렬 (\(\Sigma^{-1}\))이 됨. 즉, 이 가우시안 분포의 공분산은 \(\beta^{-1}\boldsymbol{I}\).
따라서 \((\boldsymbol{t} - \Phi\boldsymbol{w})\) 이 식에서 \(\Phi\boldsymbol{w}\) 이 부분이 가우시안 분포에서의 평균벡터이고, 공분산도 \(\beta^{-1}\boldsymbol{I}\) 이렇게 되면서 행렬이 되었음.
사전확률과 우도를 구했기 때문에 사후확률 (\(p(\boldsymbol{w}\vert \boldsymbol{t})\))을 구할 것 임.
- 복습 (가우시안 분포를 위한 베이즈 정리)
\(p(\boldsymbol{x})\) 와 \(p(\boldsymbol{y}\vert \boldsymbol{x})\) 가 다음과 같이 주어진다고 하자.
\[\begin{align} p(\boldsymbol{x}) &= \mathcal{N}(\boldsymbol{x}\vert \boldsymbol{\mu}, \Lambda^{-1}) &\leftrightarrow p(\boldsymbol{w}) &= \mathcal{N}(\boldsymbol{w}\vert \boldsymbol{m}_{0}, \boldsymbol{S}_{0}) \\ p(\boldsymbol{y}\vert \boldsymbol{x}) &= \mathcal{N}(\boldsymbol{y}\vert \boldsymbol{Ax} + \boldsymbol{b}, \boldsymbol{L}^{-1}) &\leftrightarrow p(\boldsymbol{t}\vert \boldsymbol{w}) &= \mathcal{N}(\boldsymbol{t}\vert \Phi\boldsymbol{w}, \beta^{-1}\boldsymbol{I}) \end{align}\]조건부 확률 \(p(\boldsymbol{y}\vert \boldsymbol{x})\) 의 평균과 공분산은 다음과 같다.
\[\begin{align}\mathbb{E}[\boldsymbol{x}\vert \boldsymbol{y}] &= (\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA} )^{-1}\{ \boldsymbol{A}^{T}\boldsymbol{L}(\boldsymbol{y} - \boldsymbol{b}) + \Lambda\boldsymbol{\mu} \} \\ cov[\boldsymbol{x}\vert \boldsymbol{y}] &= (\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA} )^{-1} \end{align}\]이 결과를 다음과 같이 적용한다.
\[\begin{align} \boldsymbol{x}&=\boldsymbol{w} \\ \boldsymbol{y}&=\boldsymbol{t} \\ \Lambda^{-1}&=\boldsymbol{S}_{0} \\ \boldsymbol{L}^{-1}&=\beta^{-1}\boldsymbol{I} \\ \boldsymbol{A}&=\Phi \\ \boldsymbol{\mu}&=\boldsymbol{m}_{0} \\ \end{align}\]따라서
\[\begin{align} p(\boldsymbol{w}\vert \boldsymbol{t})&=\mathcal{N}(\boldsymbol{w}\vert \boldsymbol{m}_{N}, \boldsymbol{S}_{N}) \\\\ \boldsymbol{S}_{N}&=(\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA})^{-1} \\ &=(\boldsymbol{S}_{0}^{-1} + \beta\Phi^{T}\Phi)^{-1} \\\\ \boldsymbol{S}_{N}^{-1}&=\boldsymbol{S}_{0}^{-1} + \beta\Phi^{T}\Phi \\\\ \boldsymbol{m}_{N}&=\boldsymbol{S}_{N}\{ \boldsymbol{A}^{T}\boldsymbol{L}(\boldsymbol{y} - \boldsymbol{b}) + \Lambda\boldsymbol{\mu} \} \\ &= \boldsymbol{S}_{N}\{ \Phi^{T}\beta\boldsymbol{I}\boldsymbol{t} + \boldsymbol{S}_{0}^{-1}\boldsymbol{m}_{0} \} \\ &= \boldsymbol{S}_{N}\{ \boldsymbol{S}_{0}^{-1}\boldsymbol{m}_{0} + \beta\Phi^{T}\boldsymbol{t} \} \end{align}\]\(p(\boldsymbol{w}\vert \boldsymbol{t})=\mathcal{N}(\boldsymbol{w}\vert \boldsymbol{m}_{N}, \boldsymbol{S}_{N})\)
\(\boldsymbol{w}\) 의 사후확률이 언제 최대가 될까?
\(\boldsymbol{m}_{N}\)에 해당하는 부분이 가우시안 함수의 값을 최대화시키는 \(\boldsymbol{w}\) 값이 됨.w의 사전확률을 특정한 경우를 가정했을 때, 평균벡터의 값들이 앞에서 봤던 특별한 경우들로 나타나는 경우가 있음.
사전확률의 공분산이 \(\boldsymbol{S}_{0} = \alpha^{-1}\boldsymbol{I}, \alpha \rightarrow 0\) 알파의 값이 0에 가까워질 때, \(\alpha^{-1}\boldsymbol{I}\) 이 것은 대각행렬이라 주 대각선 값이 무한히 커짐.위에서 \(\boldsymbol{S}_{N}^{-1}=\boldsymbol{S}_{0}^{-1} + \beta\Phi^{T}\Phi\)을 보면 \(\boldsymbol{S}_{0}^{-1}\)이 존재하는데, 알파가 0으로 가까워질 때 \(\boldsymbol{S}_{0}\) 이 식은 무한히 커진다고 했음. 근데 이것의 역행렬은 그럼 0에 가까워 질 것임.
그래서 결국 \(\boldsymbol{S}_{N}^{-1} \rightarrow \beta\Phi^{T}\Phi\)로 수렴을 할 것임.
\(\boldsymbol{S}_{N} = (\beta\Phi^{T}\Phi)^{-1} = \frac{1}{\beta}(\Phi^{T}\Phi)^{-1}\) 이 되기때문에 이것을 \(\boldsymbol{S}_{N}\{ \boldsymbol{S}_{0}^{-1}\boldsymbol{m}_{0} + \beta\Phi^{T}\boldsymbol{t}\}\) 이 식에 대입을 하면 됨.
\(\boldsymbol{S}_{N}\{ \boldsymbol{S}_{0}^{-1}\boldsymbol{m}_{0} + \beta\Phi^{T}\boldsymbol{t}\}\) 여기서도 \(\boldsymbol{S}_{0}^{-1}\)은 0에 가까워 지기 때문에, 결국 \(\frac{1}{\beta}(\Phi^{T}\Phi)^{-1}\beta\Phi^{T}\boldsymbol{t}\)가 됨.
베타는 cancel out, 남는 식은 \((\Phi^{T}\Phi)^{-1}\Phi^{T}\boldsymbol{t}\) 이렇게 되는데 이것은 normal equations 다. 이것은 빈도주의 방법인 Maximum Likelihood 방법을 사용했을 때 얻어지는 \(\boldsymbol{w}\)의 솔루션.
이렇듯 사전확률에서 특정한 가정을 했을 때, 사후확률이 최대화가 되는 \(\boldsymbol{w}\) 값과 동일한 결과를 얻을 수 있음.
다음과 같은 사전확률을 사용하면 식이 단순화된다.
\[p(\boldsymbol{w}\vert \alpha) = \mathcal{N}(\boldsymbol{w}\vert 0, \alpha^{-1}\boldsymbol{I})\]평균 벡터를 0, 공분산은 위와 동일하게 가정.
이 경우에 사후확률은
\[\begin{align} p(\boldsymbol{w}\vert \boldsymbol{t}) &= \mathcal{N}(\boldsymbol{w}\vert \boldsymbol{m}_{N}, \boldsymbol{S}_{N}) \\ \boldsymbol{m}_{N}&=\beta\boldsymbol{S}_{N}\Phi^{T}\boldsymbol{t} \\ \boldsymbol{S}_{N}^{-1}&=\alpha\boldsymbol{I} + \beta\Phi^{T}\Phi \end{align}\]사후확률의 로그값은 다음과 같다.
\[\ln p(\boldsymbol{w}\vert \boldsymbol{t}) = -\frac{\beta}{2}\sum_{n=1}{N}\{ \boldsymbol{t}_{n} - \boldsymbol{w}^{T}\phi(\boldsymbol{x}_{n}) \}^2 - \frac{\alpha}{2}\boldsymbol{w}^{T}\boldsymbol{w} + \text{const}\]위의 식도 자주 본 식인데, 앞의 항은 제곱합 에러, 뒷항은 규제화항이다.
이런 형태의 사전확률을 가정하게 되면, 사후확률을 최대화 시키는 \(\boldsymbol{w}\)의 값은 규제화가 포함되었을 때 에러를 최소화 시키는 값과 같아진다는 것임.
베이지안 선형회귀를 사용하게 되면, 단순하게 제곱합에러함수를 사용한다거나 규제화항을 포함한 에러를 사용할 때 얻어지는 해들이 단순히 베이지안 모델의 특수한 경우에 불과하다는 점.
베이지안 모델이 훨씬더 일반적이고 강력한 방법론임을 알 수 있음.
- 예측분포
새로운 입력 \(\boldsymbol{x}\) 가 주어졌을 때 \(\boldsymbol{t}\) 를 예측
\[p(t\vert \boldsymbol{t}, \alpha, \beta) = \int p(t\vert \boldsymbol{w}, \beta)p(\boldsymbol{w}\vert \boldsymbol{t}, \alpha, \beta)d\boldsymbol{w}\]\(\boldsymbol{t}\): 학습데이터를 관측한 값, \(t\): scalar, 새로운 예측값
\(p(\boldsymbol{x})\), \(p(\boldsymbol{y}\vert \boldsymbol{x})\) 을 알고 있을 때, 이것으로부터 \(\boldsymbol{y}\)의 주변확률(\(p(\boldsymbol{y}\))을 계산하는 공식은 \(p(\boldsymbol{y}) \rightarrow \int p(\boldsymbol{y}\vert \boldsymbol{x})p(\boldsymbol{x})d\boldsymbol{x}\) 이 적분을 하는 것이다.
위의 공식을 활용해서 \(t\)에 대해 적용하면 아래의 식이 된다.
이전 결과들을 적용해보면
\[\begin{align} p(t\vert \boldsymbol{x}, \boldsymbol{w}, \beta)&=\mathcal{N}(\boldsymbol{t}\vert \phi(\boldsymbol{x})^{T}\boldsymbol{w}, \beta^{-1}) \\ p(\boldsymbol{w}\vert \boldsymbol{t}, \boldsymbol{X}, \alpha, \beta)&=\mathcal{N}(\boldsymbol{w}\vert \boldsymbol{m}_{N}, \boldsymbol{S}_{N}) \\ \boldsymbol{x}&=\boldsymbol{w} \\ \boldsymbol{y}&=t \\ \boldsymbol{mu}&=\boldsymbol{m}_{N} \\ \Lambda^{-1}&=\boldsymbol{S}_{N} \\ \boldsymbol{A}&=\phi(\boldsymbol{x})^{T} \\ \boldsymbol{L}^{-1}&=\beta^{-1} \\ \end{align}\] \[\begin{align} p(t\vert \boldsymbol{x}, \boldsymbol{w}, \beta) &= \mathcal{N}(t\vert \boldsymbol{A\mu}+\boldsymbol{b},\boldsymbol{L}^{-1} + \boldsymbol{A}\Lambda^{-1}\boldsymbol{A}^{T}) \\ &= \mathcal{N}(t\vert \phi(\boldsymbol{x})^{T}\boldsymbol{m}_{N}, \beta^{-1}+\phi(\boldsymbol{x})^{T}\boldsymbol{S}_{N}\phi(\boldsymbol{x})) \end{align}\]Appendix
MathJax
escape unordered list
- \(cov[\boldsymbol{x}_{a}] = \Sigma_{aa}\):
\- $$cov[\boldsymbol{x}_{a}] = \Sigma_{aa}$$
\setminus
\(\{A\}\setminus\{B\}\):
$$\{A\}\setminus\{B\}$$
adjustable parenthesis
\(\left( content \right)\):
$$\left( content \right)$$
Matrix with parenthesis \(\pmatrix{a_{11} & a_{12} & \ldots & a_{1n} \cr a_{21} & a_{22} & \ldots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{m1} & a_{m2} & \ldots & a_{mn} }\):
$$\pmatrix{a_{11} & a_{12} & \ldots & a_{1n} \cr a_{21} & a_{22} & \ldots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{m1} & a_{m2} & \ldots & a_{mn} }$$
References
Pattern Recognition and Machine Learning: https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
Design Matrix: https://stats.stackexchange.com/questions/66516/meaning-of-design-in-design-matrix

Leave a comment