ML basics - Linear Models for Classification
선형분류의 목표와 방법들
분류(classification)의 목표
- 입력벡터 \(\boldsymbol{x}\)를 \(K\)개의 가능한 클래스 중에서 하나의 클래스로 할당하는 것
분류를 위한 결정이론
- 확률적 모델 (probabilistic model)
- 생성모델 (generative model): \(p(\boldsymbol{x}\vert \mathcal{C}_k)\)와 \(p(\mathcal{C}_k)\)를 모델링한다음 베이즈 정리를 사용해서 클래스의 사후 확률 \(p(\mathcal{C}_k\vert \boldsymbol{x})\)를 구한다. 또는 결합확률 \(p(\boldsymbol{x}, \mathcal{C}_k)\)을 직접 모델링할 수도 있다.
- 식별모델 (discriminative model): \(p(\mathcal{C}_k\vert \boldsymbol{x})\)를 직접적으로 모델링한다.
- 판별함수 (discriminant function): 입력 \(\boldsymbol{x}\)을 클래스로 할당하는 판별함수(discriminant function)를 찾는다. 확률값은 계산하지 않는다.
판별함수 (Discriminant functions)
입력 \(\boldsymbol{x}\)을 클래스로 할당하는 판별함수(discriminant function)를 찾고자 한다. 여기서는 그러한 함수 중 선형함수만을 다룰 것이다. 두 개의 클래스
선형판별함수는 다음과 같다.
\[y(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+w_0\]- \(\boldsymbol{w}\): 가중치 벡터 (weight vector)
- \(w_0\): 바이어스 (bias)
\(y(\boldsymbol{x}) \ge 0\) 인 경우 이를 \(\mathcal{C}_1\)으로 판별하고 아닌 경우 \(\mathcal{C}_2\)으로 판별한다.
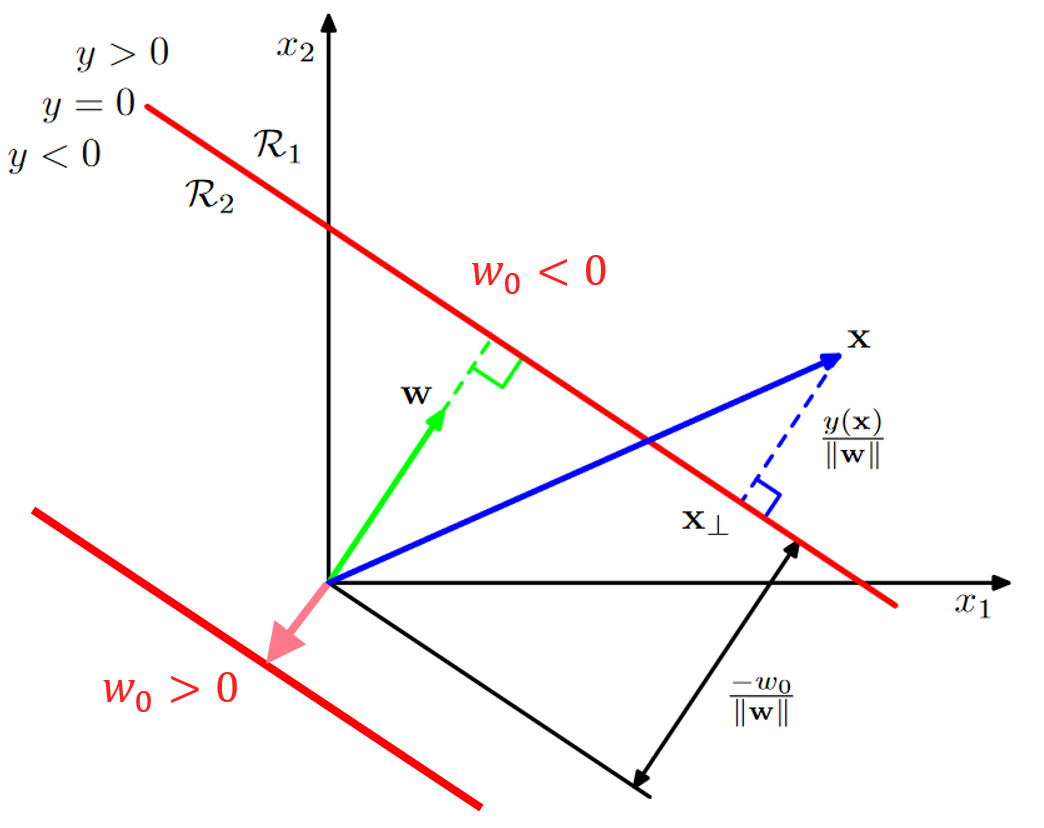
결정 경계 (decision boundary)
- \(y(\boldsymbol{x})=0\)
- \(D-1\)차원의 hyperplane (\(\boldsymbol{x}\)가 \(D\)차원의 입력벡터일 때)
\(y(\boldsymbol{x})=0\)을 만족시키는 \(\boldsymbol{x}\)의 집합을 결정 경계라고 함.
결정 경계면 위의 임의의 두 점 \(\boldsymbol{x}_A\)와 \(\boldsymbol{x}_B\)
- \(y(\boldsymbol{x}_A)=y(\boldsymbol{x}_B)=0\)
- \(\boldsymbol{w}^T(\boldsymbol{x}_A - \boldsymbol{x}_B)=0\) => \(\boldsymbol{w}\)는 결정 경계면에 수직
임의의 두 점 \(\boldsymbol{x}_A\)와 \(\boldsymbol{x}_B\)에 대해서 위의 식이 성립하기 때문에, Decision Boundary에 있는 모든 두 개의 점에 대해서 벡터 \(\boldsymbol{w}\)는 결정 경게면에 수직임.
원점에서 결정경계면까지의 거리
벡터 \(\boldsymbol{w}_{\perp}\)를 원점에서 결정 경계면에 대한 사영(projection)이라고 하자.
\[\begin{align} &\ r\frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert } = \boldsymbol{w}_{\perp}\\ &\ y(\boldsymbol{w}_{\perp}) = 0\\ &\ \boldsymbol{w}^T\boldsymbol{w}_{\perp} + w_0 = 0\\ &\ \frac{\boldsymbol{w}^T\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert }r + w_0 = 0\\ &\ \Vert \boldsymbol{w}\Vert r + w_0 = 0\\ &\ r = -\frac{w_0}{\Vert \boldsymbol{w}\Vert } \end{align}\]\(\boldsymbol{w}\)의 단위벡터 (\(\frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert }\))에 \(r\)을 곱했을때 projection vector (\(\boldsymbol{w}_{\perp}\))가 됨. 이 r를 구하면 결정경계와 원점의 거리가 됨.
projection vector (\(\boldsymbol{w}_{\perp}\))가 결정경계 위에 있기 때문에 \(y(\boldsymbol{w}_{\perp}) = 0\)가 됨.
\(\boldsymbol{w}^T\boldsymbol{w}\)은 l2 norm의 제곱 (\(\Vert \boldsymbol{w}\Vert_{2}^{2}\))이다.
따라서 \(w_0\)은 결정 경계면의 위치를 결정한다.
- \(w_0\lt0\)이면 결정 경계면은 원점으로부터 \(\boldsymbol{w}\)가 향하는 방향으로 멀어져있다.
- \(w_0\gt0\)이면 결정 경계면은 원점으로부터 \(\boldsymbol{w}\)의 반대 방향으로 멀어져있다.
여기서 중요한 부분은 결정 경계의 위치가 어디에 있느냐임. 헷갈릴 수도 있지만. bias 값이 결정경계면의 위치를 결정하는 파라미터라는 것임.
예제: \(y(x_1, x_2) = x_1 + x_2 - 1\)
또한 \(y(\boldsymbol{x})\)값은 \(\boldsymbol{x}\)와 결정 경계면 사이의 부호화된 거리와 비례한다.
\(\boldsymbol{x}-\boldsymbol{x}_\perp\)이 벡터는 \(\boldsymbol{w}\)와 방향이 같지만 길이는 r인 단위벡터임. 이것을 다시 써보면 \(\boldsymbol{x}-\boldsymbol{x}_\perp = r\frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert }\)라는 말임.
\(\boldsymbol{x} = \boldsymbol{x}_\perp + r\frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert }\) 여기에 \(\boldsymbol{w}^{T}\)를 곱하고 bias인 \(w_{0}\)을 더해줌.
\[\boldsymbol{w}^{T}\boldsymbol{x}+w_{0} = \boldsymbol{w}^{T}\boldsymbol{x}_\perp + w_{0} + r\frac{\boldsymbol{w}^{T}\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert }\]\(\boldsymbol{x}_\perp\)이 결정경계 위에 있기 때문에 \(\boldsymbol{x}_\perp + w_{0}\) 이 부분이 0이 됨. 또한 \(\frac{\boldsymbol{w}^{T}\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert }\)은 \(\Vert \boldsymbol{w}\Vert\)이 됨. 왼쪽에 있는 항은 \(y(\boldsymbol{x})\)이 됨.
따라서 \(y(\boldsymbol{x}) = r\Vert \boldsymbol{w}\Vert\)이 됨. \(r\) 곱하기 \(\boldsymbol{w}\)의 l2 norm.
다시 정리하면, \(r=\frac{y(\boldsymbol{x})}{\Vert \boldsymbol{w}\Vert }\)이 되는 것임.
임의의 한 점 \(\boldsymbol{x}\)의 결정 경계면에 대한 사영을 \(\boldsymbol{x}_\perp\)이라고 하자.
\[\boldsymbol{x}=\boldsymbol{x}_\perp + r\frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert }\] \[r=\frac{y(\boldsymbol{x})}{\Vert \boldsymbol{w}\Vert }\]좀 전에는 bias에 의해 결정경계면의 위치가 결정되었다면, 이번에는 \(y(\boldsymbol{x})\)에 의해 \(\boldsymbol{x}\)의 위치가 결정됨.
- \(y(\boldsymbol{x}) \gt 0\)이면 \(\boldsymbol{x}\)는 결정 경계면을 기준으로 \(\boldsymbol{w}\)가 향하는 방향에 있다.
- \(y(\boldsymbol{x}) \lt 0\)이면 \(\boldsymbol{x}\)는 결정 경계면을 기준으로 \(-\boldsymbol{w}\)가 향하는 방향에 있다.
- \(y(\boldsymbol{x})\)의 절대값이 클 수록 더 멀리 떨어져 있다.
가짜입력(dummy input) \(x_0=1\)을 이용해서 수식을 단순화
dummy input을 사용했다는 의미로 tilde 심볼을 사용함.
- \(\widetilde{\boldsymbol{w}}=(w_0, \boldsymbol{w})\)
- \(\widetilde{\boldsymbol{x}}=(x_0, \boldsymbol{x})\)
- \(y(\boldsymbol{x})=\boldsymbol{\widetilde{w}}^T\boldsymbol{\widetilde{x}}\)
다수의 클래스
\[y_k(\boldsymbol{x})=\boldsymbol{w}_k^T\boldsymbol{x}+w_{k0}\]\[k=1,\ldots,K\]각각의 클래스 \(k\) 마다 weight vector인 \(\boldsymbol{w}_k\)를 학습해야 함.
위와 같은 판별함수는 \(j{\neq}k\)일 때 \(y_k(\boldsymbol{x})\gt y_j(\boldsymbol{x})\)를 만족하면 \(\boldsymbol{x}\)를 클래스 \(\mathcal{C}_k\)로 판별하게 된다.
분류를 위한 최소제곱법 (Least squares for classification)
\[y_k(\boldsymbol{x})=\boldsymbol{w}_k^T\boldsymbol{x}+w_{k0}\] \[k=1,\ldots,K\]그렇다면 파라미터 \(\boldsymbol{w}\)를 어떻게 학습할 수 있을까? 간단하게 하는 법은 최소제곱법. 선형회귀에서는 목표값이 실수값으로 주어졌기 때문에, 자연스럽게 될 수 있지만, 분류에서는 실수값이긴 하지만, 만약에 2개의 클래스라면 0 or 1 으로 실수값의 목표값으로 변환시키는 방식으로 함.
결론적으로는 분류에는 별로 좋지 않은 방식이다.
아래와 같이 행렬 \(\widetilde{\boldsymbol{W}}\)을 사용하여 간편하게 나타낼 수 있다.
\[y(\boldsymbol{x}) = \widetilde{\boldsymbol{W}}^T\widetilde{\boldsymbol{x}}\]\(~~ \widetilde{\boldsymbol{W}} = \begin{bmatrix} \vert\\ \cdots \widetilde{\boldsymbol{w}}_k \cdots\\ \vert \end{bmatrix}\)인데, K=3인 경우, \(y_1(\boldsymbol{x})=\widetilde{\boldsymbol{w}}_{1}^T\widetilde{\boldsymbol{x}}\), \(y_2(\boldsymbol{x})=\widetilde{\boldsymbol{w}}_{2}^T\widetilde{\boldsymbol{x}}\), \(y_3(\boldsymbol{x})=\widetilde{\boldsymbol{w}}_{3}^T\widetilde{\boldsymbol{x}}\) 이 각각의 값들은 scalar값인데 이 것을 하나의 표현할 것임.
\(y(\boldsymbol{x}) = \begin{bmatrix} \widetilde{\boldsymbol{w}}_{1}^T\widetilde{\boldsymbol{x}}\\ \widetilde{\boldsymbol{w}}_{2}^T\widetilde{\boldsymbol{x}}\\ \widetilde{\boldsymbol{w}}_{3}^T\widetilde{\boldsymbol{x}}\\ \end{bmatrix} = \begin{bmatrix} - \widetilde{\boldsymbol{w}}_{1}^T - \\ - \widetilde{\boldsymbol{w}}_{2}^T - \\ - \widetilde{\boldsymbol{w}}_{3}^T - \\ \end{bmatrix}\widetilde{\boldsymbol{x}} = \widetilde{\boldsymbol{W}}^T\widetilde{\boldsymbol{x}}\) 이런식으로 표현되는 것임.
\(\widetilde{\boldsymbol{W}}\)의 \(k\)번째 열은 \(\widetilde{\boldsymbol{w}}_k = (w_{k0}, \boldsymbol{w}_k^T)^T\)이다.
제곱합 에러 함수
학습데이터 \(\{\boldsymbol{x}_n, \boldsymbol {T}_n\}\), \(n=1,\ldots,N\), \(n\)번째 행이 \(\boldsymbol {T}_n^T\)인 행렬 \(\boldsymbol {T}\), \(n\)번째 행이 \(\widetilde{\boldsymbol{x}}_n^T\)인 행렬 \(\widetilde{\boldsymbol{X}}\)이 주어졌을 때 제곱합 에러함수(sum-of-squared error function)은
\[E_D(\widetilde{\boldsymbol{W}}) = \frac{1}{2}\mathrm{tr}\left\{ \left(\widetilde{\boldsymbol{X}}\widetilde{\boldsymbol{W}}-\boldsymbol{T} \right)^T \left(\widetilde{\boldsymbol{X}}\widetilde{\boldsymbol{W}}-\boldsymbol{T} \right) \right\}\]유의할점은 K>2 일 경우 \widetilde{\boldsymbol{W}}가 행렬이라는 점이다. 각각의 열이 하나의 클래스에 대응함.
선형대수에서 했던 PCA와 유사함
다른식으로 정리하면, \(E_D(\widetilde{\boldsymbol{W}}) = \frac{1}{2}\Vert\widetilde{\boldsymbol{X}}\widetilde{\boldsymbol{W}} \Vert_{F}^{2}\): 행렬과 행렬의 차이에 Frobenius norm을 제곱한 것.(식을 간편하게 하기 위해 1/2 곱해줌) 이것이 \(E_D(\widetilde{\boldsymbol{W}}) = \frac{1}{2}\mathrm{tr}\left\{ \left(\widetilde{\boldsymbol{X}}\widetilde{\boldsymbol{W}}-\boldsymbol{T} \right)^T \left(\widetilde{\boldsymbol{X}}\widetilde{\boldsymbol{W}}-\boldsymbol{T} \right) \right\}\) 이 것과 동일함.
제곱합 에러를 생각할때, 행렬의 Frobenius norm을 최소화 시킨다라는 것을 생각.
로 표현할 수 있다.
아래와 같이 유도할 수 있다. Design Matrix
\[\widetilde{\boldsymbol{X}} = \begin{bmatrix} \vdots\\ - \widetilde{\boldsymbol{x}}_n^T -\\ \vdots \end{bmatrix},~~ \widetilde{\boldsymbol{W}} = \begin{bmatrix} \vert\\ \cdots \widetilde{\boldsymbol{w}}_k \cdots\\ \vert \end{bmatrix},~~ \boldsymbol {T}= \begin{bmatrix} \vdots\\ - \boldsymbol {T}_n^T -\\ \vdots \end{bmatrix}\]\[\begin{align} E_D(\widetilde{\boldsymbol{W}}) &\ = \frac{1}{2}\sum_{n=1}^N\sum_{k=1}^K \left(\widetilde{\boldsymbol{x}}_n^T\widetilde{\boldsymbol{w}}_k - \boldsymbol {T}_{nk}\right)^2\\ &\ = \frac{1}{2}\sum_{n=1}^N \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right) \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right)^T\\ &\ = \frac{1}{2}\sum_{n=1}^N \mathrm{tr}\left\{ \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right) \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right)^T \right\}\\ &\ = \frac{1}{2}\sum_{n=1}^N \mathrm{tr}\left\{ \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right)^T \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right) \right\}\\ &\ = \frac{1}{2}\mathrm{tr}\left\{ \sum_{n=1}^N \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right)^T \left( \widetilde{\boldsymbol{x}}_n^T \widetilde{\boldsymbol{W}} - \boldsymbol {T}_n^T \right) \right\}\\ &\ = \frac{1}{2}\mathrm{tr}\left\{ \left(\widetilde{\boldsymbol{x}}\widetilde{\boldsymbol{W}}-\boldsymbol {T} \right)^T \left(\widetilde{\boldsymbol{x}}\widetilde{\boldsymbol{W}}-\boldsymbol {T} \right) \right\} \end{align}\]\({T}= \begin{bmatrix} \vdots\\ - \boldsymbol {T}_n^T -\\ \vdots \end{bmatrix}\)는 각각의 행은 K개의 값들을 가진 벡터임.
마지막 과정
\[\begin{align} {\boldsymbol A} &= \boldsymbol{X}\boldsymbol{W} - \boldsymbol{T} = \begin{bmatrix} \vdots\\ - \boldsymbol{x}_n^T \boldsymbol{W} - \boldsymbol {T}_n^T-\\ \vdots \end{bmatrix}\\ {\boldsymbol A}^T{\boldsymbol A} &= \begin{bmatrix} \vert\\ \cdots \left(\boldsymbol{x}_n^T \boldsymbol{W} - \boldsymbol {T}_n^T\right)^T\cdots\\ \vert \end{bmatrix} \begin{bmatrix} \vdots\\ - \boldsymbol{x}_n^T \boldsymbol{W} - \boldsymbol {T}_n^T-\\ \vdots \end{bmatrix}\\ &= \sum_{n=1}^N \left( \boldsymbol{x}_n^T \boldsymbol{W} - \boldsymbol {T}_n^T \right)^T \left( \boldsymbol{x}_n^T \boldsymbol{W} - \boldsymbol {T}_n^T \right) \end{align}\]이 부분도 PCA 할대 했던 것임.
\(\widetilde{\boldsymbol{W}}\)에 대한 \(E_D(\widetilde{\boldsymbol{W}})\)의 최솟값을 구하면
\[\widetilde{\boldsymbol{W}}=(\widetilde{\boldsymbol{X}}^T\widetilde{\boldsymbol{X}})^{-1}\widetilde{\boldsymbol{X}}^T\boldsymbol {T}=\widetilde{\boldsymbol{X}}^{\dagger}\boldsymbol{T}\]\(\widetilde{\boldsymbol{X}}^{\dagger}\) \(\boldsymbol{X}\)의 pseudo inverse에 목표값 행렬을 곱한 것이 에러함수를 최소화 시키는 \(\boldsymbol{W}\)임.
따라서 판별함수는 다음과 같다.
\[y(\boldsymbol{x})=\widetilde{\boldsymbol{W}}^T\widetilde{\boldsymbol{x}}=\boldsymbol{T}^T\left(\widetilde{\boldsymbol{X}}^{\dagger}\right)^T\widetilde{\boldsymbol{x}}\]- 분류를 위한 최소제곱법의 문제들
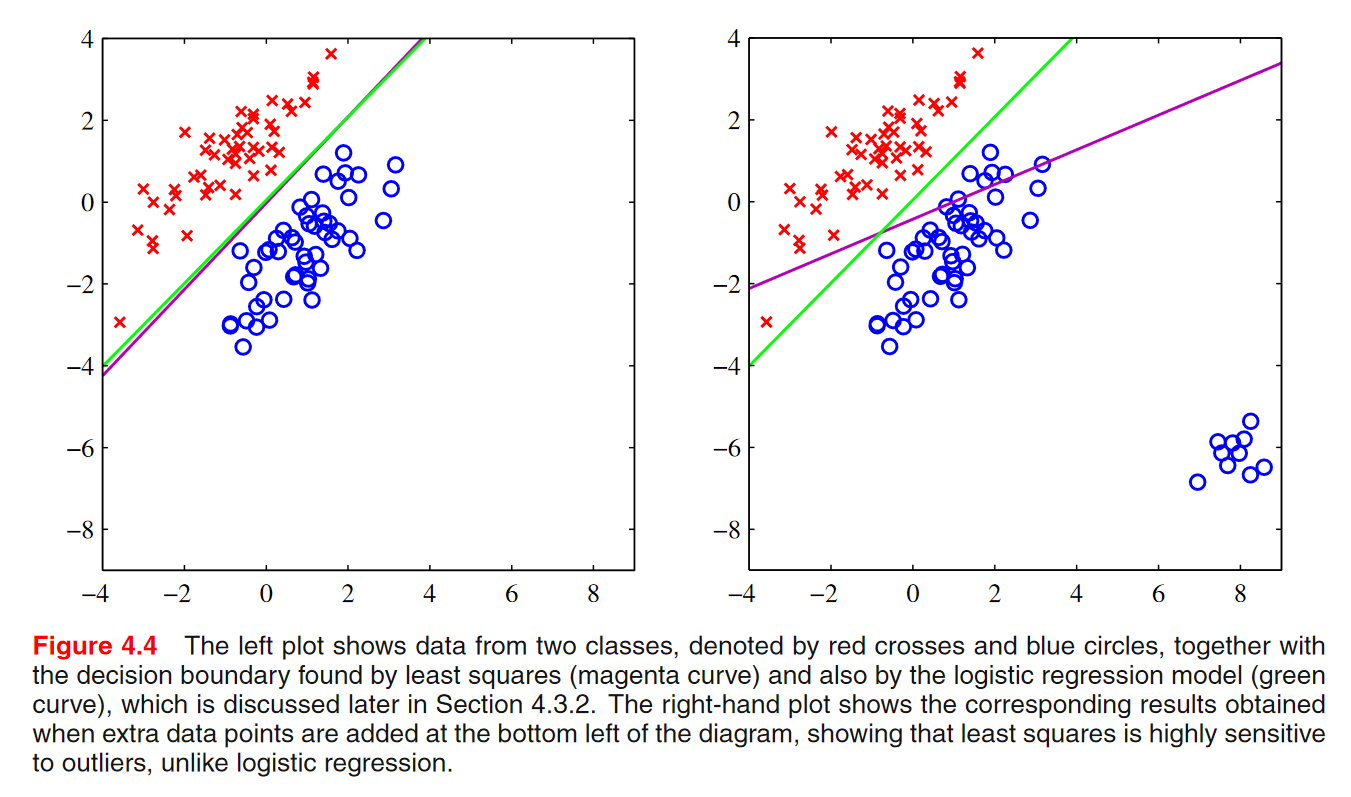
- 극단치에 민감하다.
- 목표값의 확률분포에 대한 잘못된 가정에 기초해 있다.
보라색선이 최소제곱법을 사용했을 때의 선형함수, 초록색이 로지스틱을 사용한 선형함수
목표값이 가우시안 분포를 따를 때, 최소제곱법이 쓰여질 수 있음. 분류의 경우 사실 목표값의 확률분포는 가우시안 분포를 따르지 않음. 목표값이 이산적인 값이기 때문에.
퍼셉트론 알고리즘 (The perceptron algorithm)
\[y(\boldsymbol{x})=f(\boldsymbol{w}^T\phi(\boldsymbol{x}))\]input \(\boldsymbol{x}\) 대신에 기저함수 \(\phi(\boldsymbol{x})\)를 사용하는 것.
\(\boldsymbol{w}\)에 관한 선형함수를 \(f()\)라는 함수를 통해서 output을 구함.
이러한 함수 \(f()\)를 활성함수 (Activation Function)이라고 부름.
분류문제를 위해서는 함수의 출력값이 임의의 범위에 있는 것이 아니라, 유한한 개수의 값을 가져야 하기 때문에, 일정한 범위내에 있게 만들기 위해 Activation function을 사용하는 것임.
퍼셉트론 같은 경우 계단형 활성함수를 사용함.
여기서 \(f\)는 활성 함수(activation fucntion)로 퍼셉트론은 아래와 같은 계단형 함수를 사용한다.
\[f(a)= \left\{ {\begin{array}{ll}+1, &\ a \ge 0 \\-1, &\ a \lt 0 \end{array}} \right.\]여기서 \(\phi_0(\boldsymbol{x})=1\)이다.
에러함수
\[E_P(\boldsymbol{w})=\sum_{n \in \mathcal{M}}\boldsymbol{w}^T\phi_{n}t_{n}\]\(t \in \{-1, 1 \}\) 이 두가지 값만 가진다고 가정.
최소제곱법을 사용할 때에는 {0,1}로 가정했지만, 퍼셉트론 에서는 {-1,1}, \(C_1 = 1, C_2 = -1\) 이런식으로 할당함.
이렇게 주어졌을 때, 찾고자 하는 \(\boldsymbol{w}\)는 어떤 성질을 가지냐면,
\[\begin{align} t_n &= +1 &\rightarrow \boldsymbol{w}^T\phi_{n} \gt 0 \\ t_n &= -1 &\rightarrow \boldsymbol{w}^T\phi_{n} \lt 0\end{align}\]위의 두가지 경우를 보면, 이상적인 상황에서는 \(\boldsymbol{w}^T\phi_{n}t_{n} \gt 0\) 이러한 형태가 됨. target값이 +1, -1 이던간에 0보다 커야함.
만약에 이것을 만족하지 않으면 \(\boldsymbol{w}^T\phi_{n}t_{n} \gt 0\)은 0보다 작게 됨.
에러함수를 보게 되면 \(E_P(\boldsymbol{w})=\sum_{n \in \mathcal{M}}\boldsymbol{w}^T\phi_{n}t_{n}\), 에러가 발생했다는 의미는 \(\boldsymbol{w}^T\phi_{n}t_{n}\) 이 값이 음이 된다는 의미. 에러가 발생했다면 양의 에러값이 나오게 되고 이 양의 에러값을 최소화 하는 것이 우리의 목표임.
\(\mathcal{M}\)은 잘못 분류된 데이터들의 집합
Stochastic gradient descent의 적용
\[\boldsymbol{w}^{(\tau+1)}=\boldsymbol{w}^{(\tau)}\eta\triangledown E_p(\boldsymbol{w})=\boldsymbol{w}^{(\tau)}+\eta\phi_n{t_n}\]\(\eta\triangledown E_p(\boldsymbol{w})\) 이 부분은 위의 에러함수에 의해서 \(\boldsymbol{w}\)에 관한 부분이기 때문에 \(\phi_{n}t_{n}\)만 남게 되고, 앞에 마이너스가 있기 때문에, 결국 \(+\eta\phi_n{t_n}\)가 되는 것임.
업데이트가 어떻게 적용되는 가
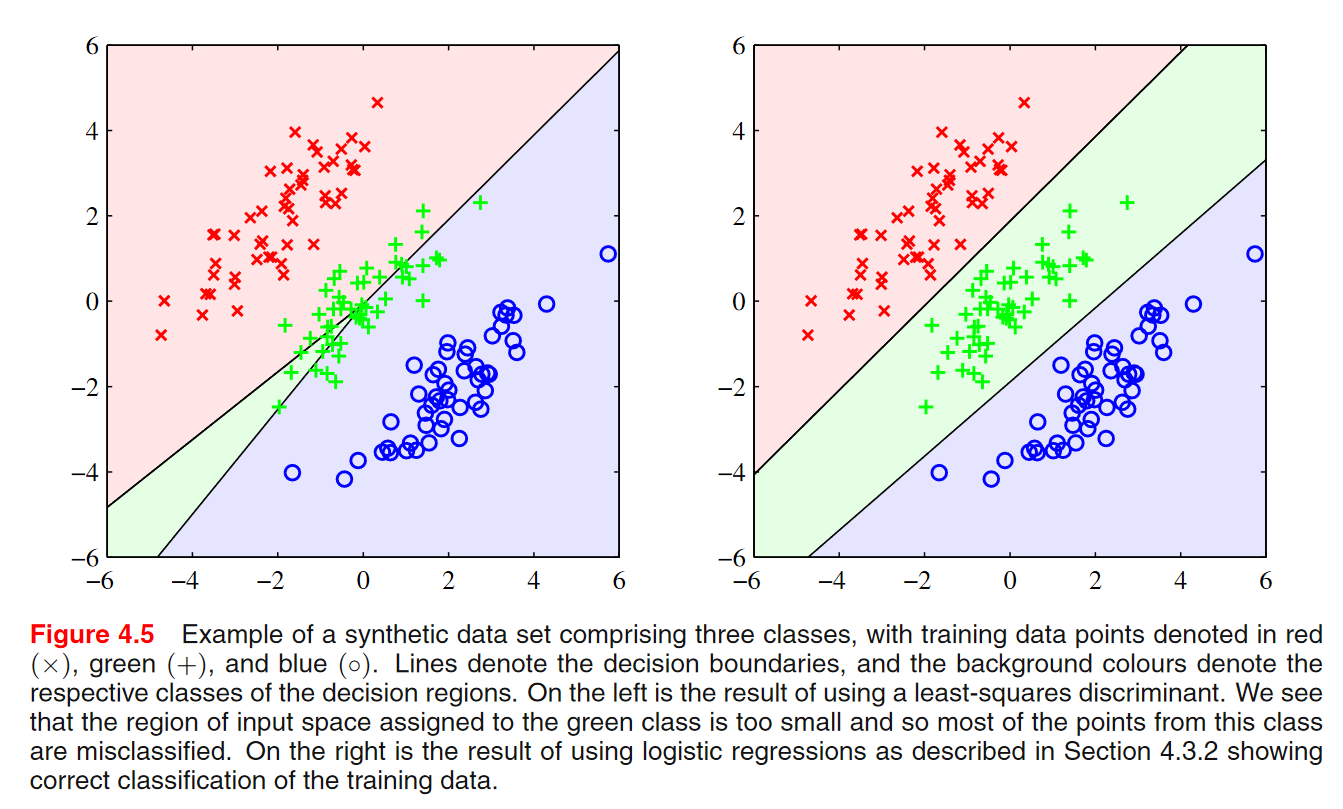
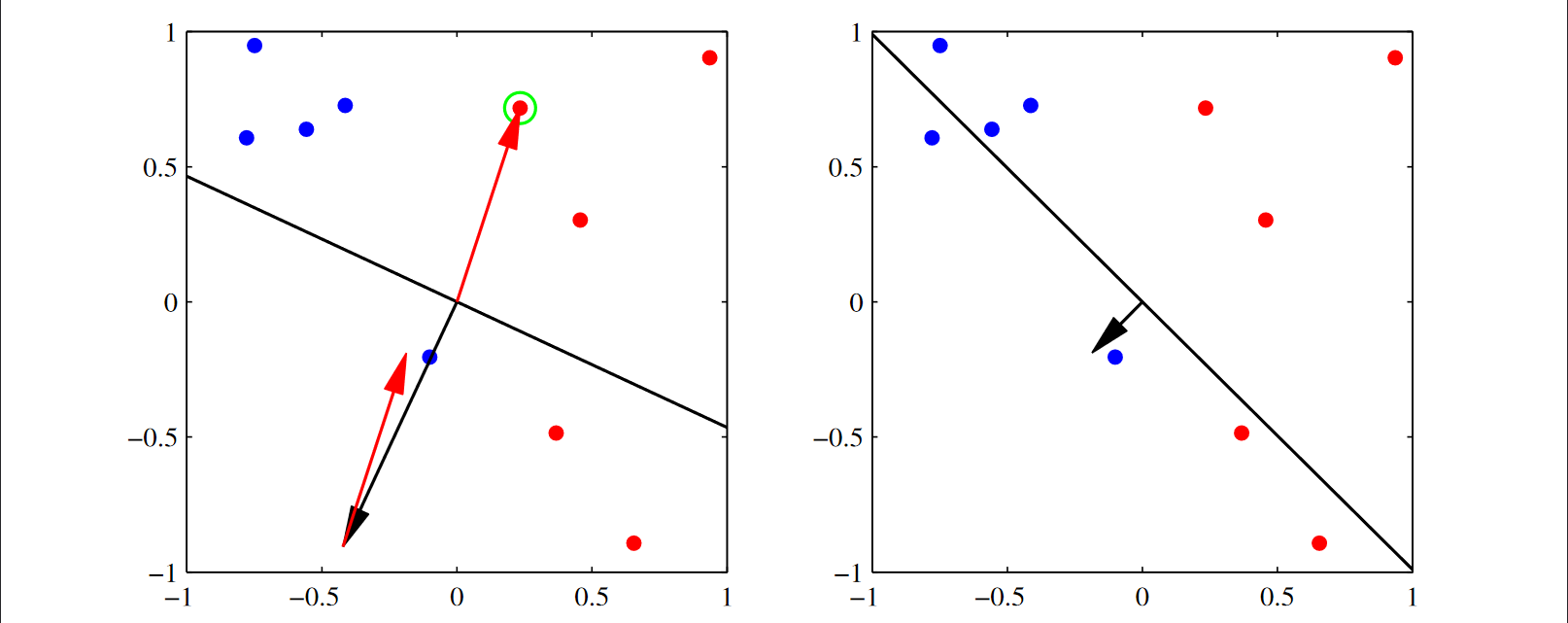
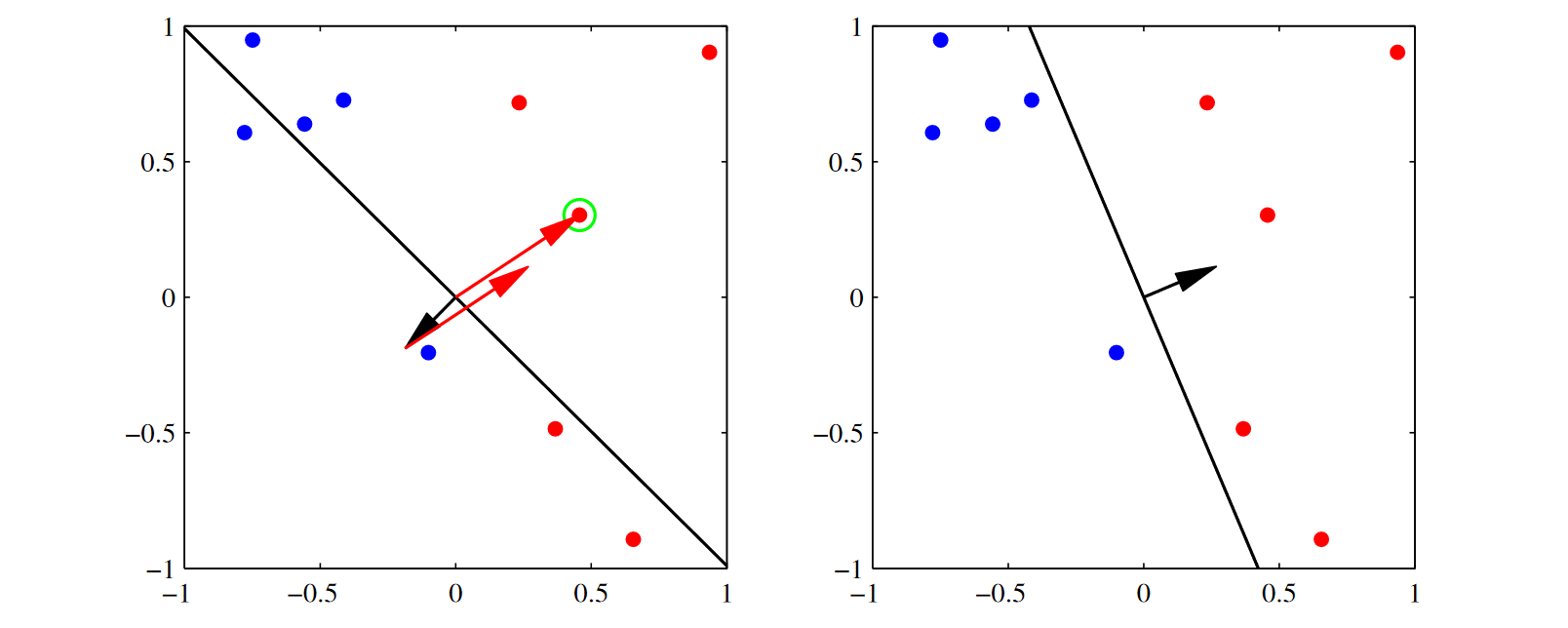
가장 이상적인 것은 (2,2)에 있는 그래프임. 검은선이 decision boundary이고 arrow가 벡터 \(\boldsymbol{w}\) 임. 우리가 원하는 것은 \(\boldsymbol{w}\)가 가리키는 방향에 빨간점이 위치해 있는 것이고, \(\boldsymbol{w}\)의 반대 쪽에 파란점 들이 있는 것임.
업데이트 할 때, 에러가 오분류된 점들에 대해서만 적용이 됨. (위에서 언급된 부분: \(\mathcal{M}\)은 잘못 분류된 데이터들의 집합)
예를 들어 아래 그림에서 (1,1)을 보면, 초록색 원으로 둘러싸인 오분류된 점에 의해서 파라미터 \(\boldsymbol{w}\)가 어떻게 업데이트 되는지를 보자.
\(\eta = 1, t_n = 1\)이라고 가정할 때, 입력값 \(\phi_n\)을 더해주는 것임. 아래를 향하고 있는 \(\boldsymbol{w}\)에다가 입력값 \(\phi_n\)을 더해주는 효과가 있는 것임. 그 결과로 벡터가 합성이 되면서 (1,2)의 모양으로 \(\boldsymbol{w}\)가 바뀐 것임.
다시 (2,1)의 그림에서 초록색 원으로 둘러싸인 오분류된 점을 선택해서 업데이트를 한다면 (2,2)의 \(\boldsymbol{w}\)의 형태로 업데이트가 됨.
위 업데이트가 실행될 때 잘못 분류된 샘플에 미치는 영향
\[\boldsymbol{w}^{(\tau+1)T}{\phi}_n{t_n} = \boldsymbol{w}^{(\tau)T}{\phi_n}{t_n}-(\phi_n{t_n})^T\phi_n{t_n} \lt \boldsymbol{w}^{(\tau)T}\phi_n{t_n}\]\(\boldsymbol{w}^{(\tau+1)T}{\phi}_n{t_n}\)은 위에서본 에러부분임. \((\phi_n{t_n})^T\phi_n{t_n}\) 이 부분은 dot product이고 이 것은 양수이기 때문에, 업데이트 후에는 에러가 줄어든 것을 의미. \(\boldsymbol{w}^{(\tau)T}{\phi_n}{t_n}-(\phi_n{t_n})^T\phi_n{t_n} \lt \boldsymbol{w}^{(\tau)T}\phi_n{t_n}\) 이 식의 업데이트 후(\(\tau+1\)) 에러가 줄어들었다는 의미
업데이트 할 때마다 그 점에 있어서는 에러가 준다는 점.

두가지 방법 판별함수 방법들은 output을 출력하지만, 그것의 확률은 계산해주지 않기 때문에 한계가 있음. 제곱합보다는 퍼셉트론이 좋은 알고리즘이라고 볼 수 있음.
퍼셉트론 방법이 뉴럴모델의 기초가 된 것임.
확률 모델
생성모델과 식별모델
확률적 생성 모델 (Probabilistic Generative Models)
판별함수 방법에서는 에러함수를 설정하고 그 에러함수를 최소화시키기 위해 최적의 파라미터를 찾는 것이 목표였음. 확률 모델은 데이터의 분포를 모델링 하면서 분류문제를 푼다.
이제 분류문제를 확률적 관점에서 살펴보고자 한다. 선형회귀와 마찬가지로 확률적 모델은 통합적인 관점을 제공해준다. 예를 들어 데이터의 분포에 관해 어떤 가정을 두게 되면 앞에서 살펴본 선형적인 결정경계(linear decision boundary)가 그 결과로 유도되는 것을 보게 될 것이다.
\(p(\boldsymbol{x}\vert \mathcal{C}_k)\)와 \(p(\mathcal{C}_k)\)를 모델링한다음 베이즈 정리를 사용해서 클래스의 사후 확률 \(p(\mathcal{C}_k\vert \boldsymbol{x})\)를 구한다. 이전의 판별함수 방법에서는 어떤 에러함수를 최소화시키기 위한 최적의 파라미터를 찾는 것이 목적이라면 확률적 모델은 데이터의 분포(클래스를 포함한)를 모델링하면서 분류문제를 결과적으로 풀게 된다.
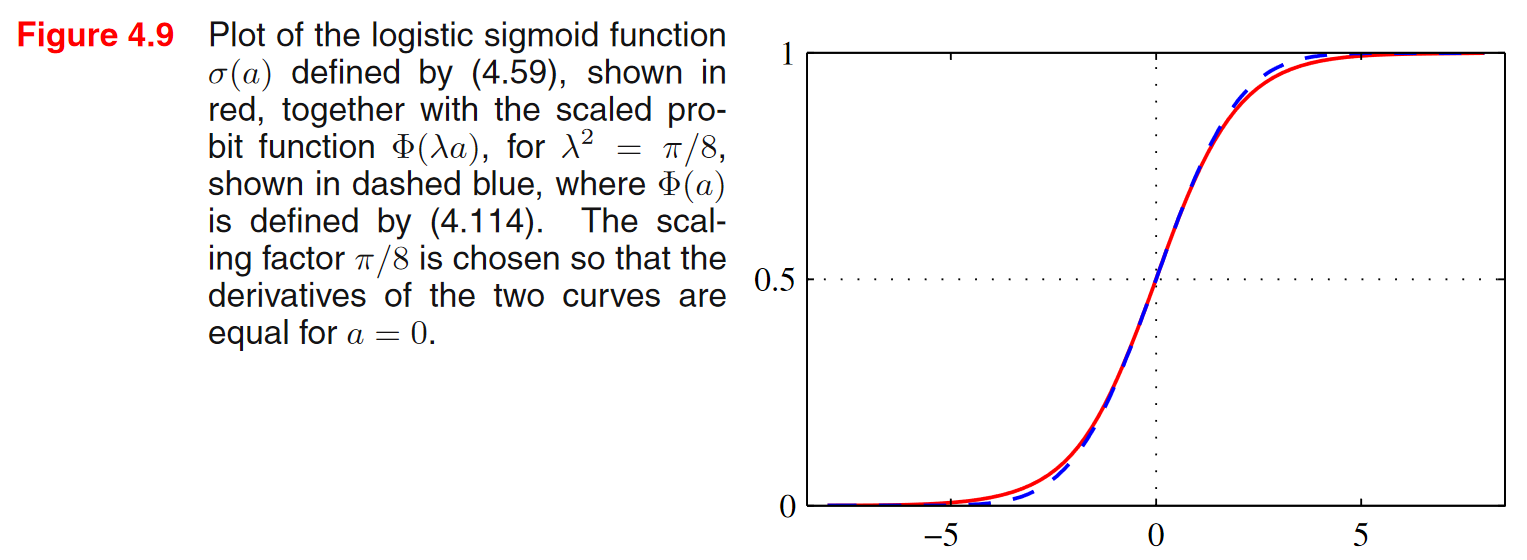
\[p(\mathcal{C}_1\vert \boldsymbol{x}) = \frac{p(\boldsymbol{x}\vert \mathcal{C}_1)p(\mathcal{C}_1)}{p(\boldsymbol{x}\vert \mathcal{C}_1)p(\mathcal{C}_1)+p(\boldsymbol{x}\vert \mathcal{C}_2)p(\mathcal{C}_2)}=\frac{1}{1+\exp(-a)} = \sigma(a)\]\(\frac{1}{1+\exp(-a)} = \sigma(a)\) a에 대한 시그모이드 함수.
\[a=\ln{\frac{p(\boldsymbol{x}\vert \mathcal{C}_1)p(\mathcal{C}_1)}{p(\boldsymbol{x}\vert \mathcal{C}_2)p(\mathcal{C}_2)}}\] \[\sigma(a)=\frac{1}{1+\exp(-a)}\]시그모이드 함수:
\(a = 0 \rightarrow \exp(a) = 1 \rightarrow \sigma(a) = 0.5\)
\(a \approx \infty \rightarrow \exp(-a) \approx -\infty \rightarrow \sigma(a) \approx 1\)
\(a \approx -\infty \rightarrow \exp(-a) \approx \infty \rightarrow \sigma(a) \approx 0\)
\(a\)가 특정한 함수형태, 예를 들어 선형함수 형태를 가지게 될 떄, 이런 모델을 generalized linear model 이라고 부른다.
왜?
Sigmoid & Logistic Function
\[\text{Logistic Function: } f(x) = \frac{L}{1+e^{-k(x-x_{0})}}\]where
- \(x_{0}\), the \(x\) value of the sigmoid’s midpoint;
- \(L\), the curve’s maximum value;
- \(k\), the logistic growth rate or steepness of the curve.
The sigmoid function is a special case of the Logistic function when \(L=1, k=1, x_0=0\).
- \(L\) is the maximum value the function can take. \(e^{−k(x−x_0)}\) is always greater or equal than 0, so the maximum point is achieved when it it 0, and is at \(L/1\).
- \(x_0\) controls where on the \(x\) axis the growth should the, because if you put \(x_0\) in the function, \(x_0−x_0\) cancel out and \(e_0=1\), so you end up with \(f(x_0)=L/2\), the midpoint of the growth.
- the parameter \(k\) controls how steep the change from the minimum to the maximum value is.
Logistic sigmoid의 성질 및 역함수
- \(\sigma(-a) = 1 - \sigma(a)\): 대칭적인 성질
- \(a=\ln\left(\frac{\sigma}{1\sigma}\right)\):역함수는 로그형태로 주어짐
\(1 - \sigma(a)\) 여기서 sigma를 delta라고 읽을 수 있음.
\(K\gt2\)인 경우
\[p(\mathcal{C}_k\vert \boldsymbol{x}) = \frac{p(\boldsymbol{x}\vert \mathcal{C}_k)p(\mathcal{C}_k)}{\sum_j{p(\boldsymbol{x}\vert \mathcal{C}_j)p(\mathcal{C}_j)}}=\frac{\exp(a_k)}{\sum_j{\exp(a_j)}}\] \[a_k = p(\boldsymbol{x}\vert \mathcal{C}_k)p(\mathcal{C}_k)\]\(a_k\) 가 이렇게 정의된다는 것을 기억하자. 클래스 k에 대한 조건부 확률 곱하기 클래스 k의 확률
연속적 입력 (continous inputs)
데이터의 분포에 대한 가정을 두게되면, 그 결과로 선형적인 결정 경계가 만들어짐.
\(p(\boldsymbol{x}\vert \mathcal{C}_k)\)가 가우시안 분포를 따르고 모든 클래스에 대해 공분산이 동일하다고 가정하자.
\[p(\boldsymbol{x}\vert \mathcal{C}_k) = \frac{1}{(2\pi)^{D/2}\vert \Sigma\vert ^{1/2}}\exp\left\{\frac{1}{2}(\boldsymbol{x}-{\pmb \mu}_k)^T\Sigma^{-1}(\boldsymbol{x}-{\pmb \mu}_k)\right\}\]공분산이 동일하다고 가정했기 때문에 k라는 subscript가 없다.
두 개의 클래스인 경우
\[p(\mathcal{C}_1\vert \boldsymbol{x}) = \sigma(a)\]\(a\)를 전개하면(k=2일 경우임)
\[\begin{align} a &\ = \ln{\frac{p(\boldsymbol{x}\vert \mathcal{C}_1)p(\mathcal{C}_1)}{p(\boldsymbol{x}\vert \mathcal{C}_2)p(\mathcal{C}_2)}}\\ &\ = - \frac{1}{2}(\boldsymbol{x}-{\pmb \mu}_1)^T\Sigma^{-1}(\boldsymbol{x}-{\pmb \mu}_1) + \frac{1}{2}(\boldsymbol{x}-{\pmb \mu}_2)^T\Sigma^{-1}(\boldsymbol{x}-{\pmb \mu}_2)+\ln\frac{p(\mathcal{C}_1)}{p(\mathcal{C}_2)}\\ &\ = \left\{\left( {\pmb \mu}_1^T - {\pmb \mu}_2^T \right)\Sigma^{-1}\right\}\boldsymbol{x} - \frac{1}{2}{\pmb \mu}_1^T\Sigma^{-1}{\pmb \mu}_1 + \frac{1}{2}{\pmb \mu}_2^T\Sigma^{-1}{\pmb \mu}_2 + \ln\frac{p(\mathcal{C}_1)}{p(\mathcal{C}_2)} \end{align}\]로그를 취하면 지수부만 남게됨, 따라서 클래스 1에 대한 이차형식과 클래스 2에 대한 이차형식 두 부분만 남게됨.
\(- \frac{1}{2}(\boldsymbol{x}-{\pmb \mu}_1)^T\), \(\frac{1}{2}(\boldsymbol{x}-{\pmb \mu}_2)\) 여기 부호를 보면 \(\mu_1\)에 대해서는 마이너스 인데, \(\mu_1\)에 대해서는 플러스임.
그리고, 이차형식에서 \(\boldsymbol{x}\) 관련된 부분은 공분산이 동일하게 때문에 서로 cancel out.
따라서 \(a\)를 \(\boldsymbol{x}\)에 관한 선형식으로 다음과 같이 정리할 수 있다.
\[p(\mathcal{C}_1\vert \boldsymbol{x}) = \sigma(\boldsymbol{w}^T\boldsymbol{x}+w_0)\] \[\begin{align} \boldsymbol{w} &\ = \Sigma^{-1}({\pmb \mu}_1 - {\pmb \mu}_2)\\ w_0 &\ = - \frac{1}{2}{\pmb \mu}_1^T\Sigma^{-1}{\pmb \mu}_1 + \frac{1}{2}{\pmb \mu}_2^T\Sigma^{-1}{\pmb \mu}_2 + \ln\frac{p(\mathcal{C}_1)}{p(\mathcal{C}_2)} \end{align}\]위의 식 \(\left\{\left( {\pmb \mu}_1^T - {\pmb \mu}_2^T \right)\Sigma^{-1}\right\}\boldsymbol{x} - \frac{1}{2}{\pmb \mu}_1^T\Sigma^{-1}{\pmb \mu}_1 + \frac{1}{2}{\pmb \mu}_2^T\Sigma^{-1}{\pmb \mu}_2 + \ln\frac{p(\mathcal{C}_1)}{p(\mathcal{C}_2)}\)을 선형식으로 바꾸면,
\(\begin{align} \boldsymbol{w} &\ = \Sigma^{-1}({\pmb \mu}_1 - {\pmb \mu}_2)\\ w_0 &\ = - \frac{1}{2}{\pmb \mu}_1^T\Sigma^{-1}{\pmb \mu}_1 + \frac{1}{2}{\pmb \mu}_2^T\Sigma^{-1}{\pmb \mu}_2 + \ln\frac{p(\mathcal{C}_1)}{p(\mathcal{C}_2)} \end{align}\) 이러한 형태가 되는 것임.
\(p(\mathcal{C}_1\vert \boldsymbol{x}) = \sigma(\boldsymbol{w}^T\boldsymbol{x}+w_0)\) 식을보면, 시그모이드 함수를 거치지만 \(\boldsymbol{x}\)에 관한 선형식의 형태로 표현이 됨.
결국에 확률이 가지는 decision boundary는 결국 \(\boldsymbol{x}\)에 관한 선형식에 의해서 결정됨.
\(K\)개의 클래스인 경우
\[\boldsymbol{w}_k = \Sigma^{-1}{\pmb \mu}_k\] \[w_{k0} = \frac{1}{2}{\pmb \mu}_{k}^{T}\Sigma^{-1}{\pmb \mu}_k + \ln p(\mathcal{C}_k)\]\(a_k = \ln p(\boldsymbol{x}\vert \mathcal{C}_k)p(\mathcal{C}_k)\), \(p(\mathcal{C}_k\vert \boldsymbol{x}) = \frac{\exp(a_k)}{\sum_j{\exp(a_j)}}\)
위의 정의와 가우시안분포를 활용하면,
\[\begin{align} a_k &= \ln(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma\vert ^{1/2}}) - \frac{1}{2}(\boldsymbol{x}-{\pmb \mu}_k)^T\Sigma^{-1}(\boldsymbol{x}-{\pmb \mu}_k) + \ln p(\mathcal{C}_k) \\ &= \ln(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma\vert ^{1/2}}) - \frac{1}{2}\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{x} + \boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{x} - \frac{1}{2}\boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{\mu}_{k} + \ln p(\mathcal{C}_k) \end{align}\]이것을 다시 x에 대한 조건부 확률인 \(p(\mathcal{C}_k\vert \boldsymbol{x})\)에 대입을 해보면,
\[p(\mathcal{C}_k\vert \boldsymbol{x}) = \frac{\exp(a_k)}{\sum_j{\exp(a_j)}} = \frac{\exp\{ \ln(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma\vert ^{1/2}}) - \frac{1}{2}\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{x} \} \exp\{ \boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{x} - \frac{1}{2}\boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{\mu}_{k} + \ln p(\mathcal{C}_k) \}}{\sum_j{\exp(a_j)}}\]이 형태를 보면, \(\exp\{ \ln(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma\vert ^{1/2}}) - \frac{1}{2}\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{x} \} \exp\{ \boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{x} - \frac{1}{2}\boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{\mu}_{k} + \ln p(\mathcal{C}_k) \}\) 이 부분은 분모에도 각각의 있는 \(a_j\)에 대해서도 나타나는 동일한 부분이 될 것임. 왜냐면, 모든 클래스에 대해서 공분산이 동일하기 때문에, \(\exp\{ \ln(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma\vert ^{1/2}}) - \frac{1}{2}\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{x} \}\) 이 부분을 분자, 분모에 다 나눠주면 cancel out되고, 남는 부분은 \(\exp\{ \boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{x} - \frac{1}{2}\boldsymbol{\mu}_{k}^{T}\Sigma^{-1}\boldsymbol{\mu}_{k} + \ln p(\mathcal{C}_k) \}\) 이 것임. 남은 부분은 \(\boldsymbol{x}\)에 대한 일차형식만 살아남게 됨.
K개의 클래스일 경우에도, 2개의 클래스의 경우와 마찬가지로, Decision Boundary는 \(\boldsymbol{x}\)에 대한 선형식으로 나타남을 볼 수 있음.
이렇게 선형식으로 나타나는 이유가 공분산 (\(\Sigma\))를 모든 클래스에 대해 동일하다고 가정했기 때문에, 이러한 선형 Decision Boundary가 나타남.
만약 모든 클래스들이 공분산을 공유하지 않는다면, 이처럼 선형이 아니라 이차형식이 됨을 알 수 있음.
최대우도해 (Maximum likelihood solution)
이제 MLE를 통해 모델 파라미터들을 구해보자. 두 개의 클래스인 경우를 살펴본다.
데이터
- \(\{\boldsymbol{x}_n, t_n\}\), \(n=1,\ldots,N\).
- \(t_n=1\)은 클래스 \(\mathcal{C}_1\)을 \(t_n=0\)은 클래스 \(\mathcal{C}_2\)를 나타낸다고 하자.
파라미터들
- \(p(\mathcal{C}_1)=\pi\)라고 두면, 구해야 할 파라미터들은 \({\pmb \mu}_1\), \({\pmb \mu}_2\), \(\Sigma\), \(\pi\)이다.
우도식 유도
- \(t_n=1\)이면
\[p(\boldsymbol{x}_n, \mathcal{C}_1) = p(\mathcal{C}_1)p(\boldsymbol{x}_n\vert \mathcal{C}_1) = \pi \mathcal{N}(\boldsymbol{x}_n\vert \mu_1, \Sigma)\]- \(t_n=0\)이면
\[p(\boldsymbol{x}_n, \mathcal{C}_2) = p(\mathcal{C}_2)p(\boldsymbol{x}_n\vert \mathcal{C}_2) = (1 - \pi) \mathcal{N}(\boldsymbol{x}_n\vert \mu_2, \Sigma)\]따라서 우도함수는
\[p(\boldsymbol {t}\vert \pi, {\pmb \mu}_1, {\pmb \mu}_2, \Sigma) = \prod_{n=1}^N\left[\pi \mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)\right]^{t_n}\left[(1 - \pi)\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_2, \Sigma)\right]^{1-t_n}\] \[\boldsymbol {t} = (t_1,\ldots,t_N)^T\]\(t_n\)이 0이면 뒷부분이, \(t_n\)이 1이면 앞부분만 남기 때문에 베르누이 분포와 유사한 형태임.
\(\boldsymbol {t}\)는 N개의 목표값.
ML - \(\pi\) 구하기
위에서 \(p(\mathcal{C}_1)=\pi\)이라고 정의했음.
\(\prod_{n=1}^N\left[\pi \mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)\right]^{t_n}\left[(1 - \pi)\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_2, \Sigma)\right]^{1-t_n}\)에 로그를 씌우기 때문에, 합의 형태로 나온다.
로그를 씌우면 \(\sum_{n=1}^{N} \left[ t_n(\ln\pi + \ln\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)) + (1-t_n)(\ln(1-\pi) + \ln\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_2, \Sigma)) \right]\) 이렇게 나옴.
위의 식에서 \(\pi\) 관련항들만 모으면 아래의 식이 됨.
로그우도함수에서 \(\pi\) 관련항들만 모으면
\[\sum_{n=1}^{N}\left\{ t_n\ln\pi + (1-t_n)\ln(1-\pi) \right\}\]이 식을 \(\pi\)에 관해 미분하고 0으로 놓고 풀면
\[\pi = \frac{1}{N}\sum_{n=1}^{N}t_n = \frac{N_1}{N} = \frac{N_1}{N_1+N_2}\]\(\pi\)에 관해 미분하면, \(\sum_{n=1}^{N}\left\{ \frac{t_n}{\pi} + \frac{(1-t_n)}{(1-\pi)}(-1) \right\}\) 이렇게 됨.
0으로 놓고 풀면,
\(\begin{align} \sum_{n=1}^{N}\left\{ \frac{t_n}{\pi} + \frac{(1-t_n)}{(1-\pi)}(-1) \right\} &= 0 \\ \sum_{n=1}^{N}\frac{t_n}{\pi} &= \sum_{n=1}^{N}\frac{(1-t_n)}{(1-\pi)} \\ \frac{1}{\pi}\sum_{n=1}^{N}t_n &= \frac{1}{1-\pi}\sum_{n=1}^{N}(1-t_n) \end{align}\)
\(\sum_{n=1}^{N}t_n\) 이 값을 \(N_1\) (관측한 목표값들 중에서 클래스 1이 나타난 횟수) 으로 정의하고, \(N_2\) 는 전체 관측 횟수 \(N\)에서 \(N_1\)을 뺀 값이라고 정의하면
\(\frac{1}{\pi}N_1 = \frac{1}{1-\pi}N_2\)이다. 이식을 \(\pi\)로 표현하면 아래와 같이 됨.
이 ML 솔루션은 빈도주의적 입장에서 실제로 전체 관측한 횟수 중에서 \(C_1\)이 나타난 빈도수를 계산한 결과와 동일함.
\(N_1\)은 \(\mathcal{C}_1\)에 속하는 샘플의 수이고 \(N_2\)는 \(\mathcal{C}_2\)에 속하는 샘플의 수이다.
ML - \({\pmb \mu}_1\), \({\pmb \mu}_2\) 구하기
\({\pmb \mu}_1\) 관련항들
\[\sum_{n=1}^{N}t_n\ln \mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma) = \frac{1}{2}\sum_{n=1}^{N}t_n(\boldsymbol{x}_n-{\pmb \mu}_1)^T\Sigma^{-1}(\boldsymbol{x}_n-{\pmb \mu}_1) + \mathrm{const}\]\({\pmb \mu}_1\) 관련에 관련된 부분은 위의 로그우도함수 (\(\sum_{n=1}^{N} \left[ t_n(\ln\pi + \ln\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)) + \ldots \right]\)) 에서 \(\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)\) 이 부분임. 여기에 앞에 있는 \(\sum_{n=1}^{N}t_n\ln\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)\) 이 부분만 가져온 것이 아래의 식임.
\(\sum_{n=1}^{N}t_n\ln \mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)\)을 가우시안 함수를 사용해서 전개하면 위의이차형식이 나옴.
이 식을 \({\pmb \mu}_1\)에 관해 미분하고 0으로 놓고 풀면
\[{\pmb \mu}_1=\frac{1}{N_1}\sum_{n=1}^{N}t_n\boldsymbol{x}_n\]\({\pmb \mu}_1\)에 관해 미분하면, \(-\frac{1}{2}\sum_{n=1}^{N}t_n\left( \boldsymbol{x}_n^T\Sigma^{-1}\boldsymbol{x}_n - 2\boldsymbol{x}_n^T\Sigma^{-1}\boldsymbol{\mu}_1 + \boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1 \right)\)
\({\pmb \mu}_1\)에 관한 항만 놔두면,
\(-\frac{1}{2}\sum_{n=1}^{N}t_n\left( - 2\boldsymbol{x}_n^T\Sigma^{-1}\boldsymbol{\mu}_1 + \boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1 \right)\)이 식만 미분을 하면 됨.
행렬미분에서 \(\nabla_x b^Tx = b\) 이 성질을 활용해서 , \(- 2\boldsymbol{x}_n^T\Sigma^{-1}\boldsymbol{\mu}_1\) 이 식을 \(\boldsymbol{\mu}_1\)에 대해서 미분하면,
transpose한 값만 남게 되므로, \(-2\Sigma^{-1}\boldsymbol{x}_n\)이 됨. (\(\Sigma\)는 대칭행렬이기 때문에 tranpose해도 그대로임)뒷항인 \(\boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1\) 이 이차형식을 행렬미분의 성질 (\(\nabla_x x^TAx = 2Ax\))을 활용해서 미분하게 되면, \(2\Sigma^{-1}\boldsymbol{\mu}_1\)이 됨.
따라서, \({\pmb \mu}_1\)에 관해 미분후에는, \(-\frac{1}{2}\sum_{n=1}^{N}t_n\left( -2\Sigma^{-1}\boldsymbol{x}_n + 2\Sigma^{-1}\boldsymbol{\mu}_1 \right)\) 이 식이 나옴.
다시 정리하면, \(\sum_{n=1}^{N}t_n\left(\Sigma^{-1}\boldsymbol{x}_n - \Sigma^{-1}\boldsymbol{\mu}_1 \right)\) 최종적으로 이 식이 도출됨.
이것을 0으로 놓고 풀면,
\(\sum_{n=1}^{N}t_n\boldsymbol{x}_n = \sum_{n=1}^{N}t_n\boldsymbol{\mu}_1\)앞에서 \(\sum_{n=1}^{N}t_n\)을 \(N_1\)으로 정의한 것을 사용하면,
\(\sum_{n=1}^{N}t_n\boldsymbol{x}_n = N_1\boldsymbol{\mu}_1\)\({\pmb \mu}_1=\frac{1}{N_1}\sum_{n=1}^{N}t_n\boldsymbol{x}_n\) 이 됨.
유사하게
\[{\pmb \mu}_2=\frac{1}{N_2}\sum_{n=1}^{N}(1-t_n)\boldsymbol{x}_n\]ML - \(\Sigma\) 구하기
\[\begin{align} &\ - \frac{1}{2}\sum_{n=1}^{N}t_n\ln \vert \Sigma\vert - \frac{1}{2}\sum_{n=1}^{N}t_n(\boldsymbol{x}_n-{\pmb \mu}_1)^T\Sigma^{-1}(\boldsymbol{x}_n-{\pmb \mu}_1)\\ &\ - \frac{1}{2}\sum_{n=1}^{N}(1-t_n)\ln \vert \Sigma\vert - \frac{1}{2}\sum_{n=1}^{N}(1-t_n)(\boldsymbol{x}_n-{\pmb \mu}_2)^T\Sigma^{-1}(\boldsymbol{x}_n-{\pmb \mu}_2)\\ &\ = \frac{N}{2}\ln \vert \Sigma\vert - \frac{N}{2}\mathrm{tr}\left(\Sigma^{-1}\boldsymbol{S}\right) \end{align}\]앞에서한 가우시안 분포에서 최대우도해를 찾은 것들을 활용할 것임.
우도식에서 \(\Sigma\)와 관련된 부분을 찾아봄.\(\text{ML Solution} = \prod_{n=1}^N\left[\pi \mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_1, \Sigma)\right]^{t_n}\left[(1 - \pi)\mathcal{N}(\boldsymbol{x}_n\vert {\pmb \mu}_2, \Sigma)\right]^{1-t_n}\) 여기서 각 [] 안에 \(\Sigma\)와 관련된 부분이 있음.
이 것을 정리하면 아래와 같이 총 4가지 항이 나타남.
\[\begin{align} \boldsymbol{S} &\ =\frac{N_1}{N}\boldsymbol{S}_1+\frac{N_2}{N}\boldsymbol{S}_2\\ \boldsymbol{S}_1 &\ = \frac{1}{N_1}\sum_{n \in \mathcal{C}_1} (\boldsymbol{x}_n-{\pmb \mu}_1)(\boldsymbol{x}_n-{\pmb \mu}_1)^T\\ \boldsymbol{S}_2 &\ = \frac{1}{N_2}\sum_{n \in \mathcal{C}_2} (\boldsymbol{x}_n-{\pmb \mu}_2)(\boldsymbol{x}_n-{\pmb \mu}_2)^T \end{align}\]\(- \frac{1}{2}\sum_{n=1}^{N}t_n\ln \vert \Sigma\vert\)와 \(- \frac{1}{2}\sum_{n=1}^{N}(1-t_n)\ln \vert \Sigma\vert\)은 cancel out되고, 남는 부분인 \(- \frac{1}{2}\sum_{n=1}^{N}\ln \vert \Sigma\vert\)은 \(- \frac{N}{2}\ln \vert \Sigma\vert\)이 됨.
나머지 항들은 2개의 이차형식 \(- \frac{1}{2}\sum_{n=1}^{N}t_n(\boldsymbol{x}_n-{\pmb \mu}_1)^T\Sigma^{-1}(\boldsymbol{x}_n-{\pmb \mu}_1)\)과 \(- \frac{1}{2}\sum_{n=1}^{N}(1-t_n)(\boldsymbol{x}_n-{\pmb \mu}_2)^T\Sigma^{-1}(\boldsymbol{x}_n-{\pmb \mu}_2)\)이 있음.
이차형식의 식을 보면, 양쪽 모두 N개의 합이 있음. 2N개 만큼의 합이 있음. 이것을 다르게 표현하면, N개의 합으로 표현이 가능함. 각각의 N에 대해서 둘중의 하나만 살아남고 나머지는 0이 됨. 실제로 남게 되는 항의 개수는 위의 2개의 이차형식 중에서 살아남는 항은 N개가 됨. 이 N개 중에서 N_1만큼의 클래스 1에 관련된 항들, N_2만큼의 클래스 2에 관련된 항들이 남게 될 것임. 결국에는 N개의 합으로 표현될 수 있음. 아래 \(\boldsymbol{S}\)를 N개의 합으로 표현한 것임.\(\boldsymbol{S}_1\), \(\boldsymbol{S}_2\) 를 보면, 각각 \(\mathcal{C}_1\), \(\mathcal{C}_2\)로 표현 됨. 결국 N개의 합으로 표현이 가능함. 그렇게 하게되면 앞에서 사용한, 가우시안 분포의 최대우도를 구할때 공분산 행렬(\(\Sigma_{ML}\))을 보면,
\(l(\Lambda) = \frac{N}{2}\ln\vert \Lambda\vert - \frac{1}{2}\sum_{n=1}^{N}tr((\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\Lambda) = \frac{N}{2}\ln\vert \Lambda\vert - \frac{1}{2}tr(\boldsymbol{S}\Lambda)\)
\(\frac{N}{2}\ln\vert \Lambda\vert\) 여기에서, \(\Lambda\) 대신에 \(\Sigma\)를 사용하면 마이너스가 없어지고 동일한 식임.
뒤의 식 \(\frac{1}{2}tr(\boldsymbol{S}\Lambda\)도 \(N\)을 곱하고 \(tr\)안에다 \(\frac{1}{N}\)을 넣으면 \(\boldsymbol{S} =\frac{N_1}{N}\boldsymbol{S}_1+\frac{N_2}{N}\boldsymbol{S}_2\)와 동일하다는 것을 알 수 있음.
가우시안 분포의 최대우도를 구하는 방법을 그대로 쓰면 결국은
\[\Sigma = \boldsymbol{S}\]복습 - 가우시안 분포의 최대우도 (Maximum Likelihood for the Gaussian)
다음으로 우도를 최대화하는 공분산행렬 \(\Sigma_{ML}\)을 찾아보자.
\[l(\Lambda) = \frac{N}{2}\ln\vert \Lambda\vert - \frac{1}{2}\sum_{n=1}^{N}tr((\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\Lambda) = \frac{N}{2}\ln\vert \Lambda\vert - \frac{1}{2}tr(\boldsymbol{S}\Lambda)\] \[\boldsymbol{S} = \sum_{i=1}^{N}(\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\] \[\frac{\partial l(\Lambda)}{\partial \Lambda} = \frac{N}{2}(\Lambda^{-1})^{T}-\frac{1}{2}\boldsymbol{S}^{T} = 0\] \[(\Lambda_{ML}^{-1}) = \Sigma_{ML} = \frac{1}{N}\boldsymbol{S}\] \[\Sigma_{ML} = \frac{1}{N}\sum_{i=1}^{N}(\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\]위의 식 유도를 위해 아래의 기본적인 선형대수 결과를 사용하였다.
- \(\vert \boldsymbol{A}^{-1}\vert = l/\vert \boldsymbol{A}\vert\)
- \(\boldsymbol{x}^{T}\boldsymbol{Ax} = tr(\boldsymbol{x}^{T}\boldsymbol{Ax}) = tr(\boldsymbol{xx}^{T}\boldsymbol{A}) \)
- \(tr(\boldsymbol{A}) + tr(\boldsymbol{B}) = tr(\boldsymbol{A}+\boldsymbol{B}) \)
- \(\frac{\partial}{\partial\boldsymbol{A}}tr(\boldsymbol{BA}) = \boldsymbol{B}^{T} \)
- \(\frac{\partial}{\partial\boldsymbol{A}}\ln\vert \boldsymbol{A}\vert = (\boldsymbol{A}^{-1})^{T}\)
입력이 이산값일 경우 (Discrete features)
각 특성 \(x_i\)가 0과 1중 하나의 값만을 가질 수 있는 경우
클래스가 주어졌을 때 특성들이 조건부독립(conditional independence)이라는 가정을 할 경우 문제는 단순화된다. 이것을 naive Bayes가정이라고 한다. 이 때 \(p(\boldsymbol{x}\vert \mathcal{C}_k)\)는 다음과 같이 분해된다.
\[p(\boldsymbol{x}\vert \mathcal{C}_k) = \prod_{i=1}^{D}\mu_{ki}^{x_i}(1\mu_{ki})^{1-x_i}\]\(\mathcal{C}_k\)가 주어졌을 때, 아래처럼 쉽게 분해(Decompose)가 됨.
\(\mu_{ki} = p(x_{i}\vert \mathcal{C}_k)\)
따라서,
\[a_k(\boldsymbol{x})=\ln p(\boldsymbol{x}\vert \mathcal{C}_k)p(\mathcal{C}_k)\] \[a_k(\boldsymbol{x})=\sum_{i=1}^{D}\left\{x_i\ln \mu_{ki}+(1-x_i)\ln(1 - \mu_{ki})\right\}+\ln p(\mathcal{C}_k)\]위의 식은 \(\boldsymbol{x}\)에 관해서 linear한 식이 됨.
입력값이 이산값일 경우에도 조건부독립(conditional independence)이라는 가정을 할 경우 Decision Boundary가 여전히 선형이 된다는 것을 알 수 있음.
확률적 식별 모델 (Probabilistic Discriminative Models)
앞의 생성모델에서는 \(p(\mathcal{C}_k\vert \boldsymbol{x})\)를 \(\boldsymbol{x}\)의 선형함수가 logistic sigmoid 또는 softmax를 통과하는 식으로 표현되는 것을 보았다. 즉, K=2인 경우
\[p(\mathcal{C}_1\vert \boldsymbol{x}) = \sigma(\boldsymbol{w}^T\boldsymbol{x}+w_0)\]그리고 파라미터들 \(\boldsymbol{w}\)와 \(w_0\)를 구하기 위해서 확률분포들 \(p(\boldsymbol{x}\vert \mathcal{C}_k)\), \(p(\mathcal{C}_k)\)의 파라미터들을 MLE로 구했다.
파라미터의 개수가 비교적 많기 때문에 효율적인 방법은 아래와 같음.
대안적인 방법은 \(p(\mathcal{C}_k\vert \boldsymbol{x})\)를 \(\boldsymbol{x}\)에 관한 함수로 파라미터화 시키고 이 파라미터들을 직접 MLE를 통해 구하는 것이다.
이제부터는 입력벡터 \(\boldsymbol{x}\)대신 비선형 기저함수(basis function)들 \(\phi(\boldsymbol{x})\)를 사용할 것이다.
이런식으로 \(\boldsymbol{x}\)가 주어졌을 때 클래스의 확률을 \(\boldsymbol{x}\)에 관한 함수로 파라미터화 시킨것으로 가정하고 이 파리미터를 바로 구하는 방법이 확률적 식별 모델임.
대표적 방법이 로지스틱 회귀임.
로지스틱 회귀 (Logistic regression)
\(\boldsymbol{x}\)대신 \(\phi\)를 사용할 것임. \(\phi\)을 입력 벡터라고 생각하면 됨.
클래스 \(\mathcal{C}_1\)의 사후확률은 특성벡터 \(\phi\)의 선형함수가 logistic sigmoid를 통과하는 함수로 아래와 같이 표현된다.
\[p(\mathcal{C}_1\vert \phi)=y(\phi)=\sigma(\boldsymbol{w}^T\phi)\] \[\sigma(a)=\frac{1}{1+\exp(-a)}\] \[p(\mathcal{C}_2\vert \phi) = 1 - p(\mathcal{C}_1\vert \phi)\]\(\phi\)가 \(M\) 차원이라면 구해야 할 파라미터(\(\boldsymbol{w}\))의 개수는 \(M\)개이다. 생성모델에서는 \(M(M+5)/2+1\)개의 파라미터를 구해야 한다.
특히, 공분산 행렬에 나타나는 파라미터들을 구해야 하는데 M에 대해서 quadratic.
로지스틱 회귀에서는 M의 liear개수의 파라미터만 구해도 됨.
최대우도해
- 데이터셋: \(\{\phi_n, t_n\}\), \(n=1,\ldots,N\)
- \(t_n \in \{0, 1\}\)
- \(\boldsymbol{t} = (t_1,\ldots,t_N)^T\)
- \(\phi_n = \phi(\boldsymbol{x}_n)\)
- \(y_n = p(\mathcal{C}_1\vert \phi_n)\)
우도함수는
\[p(\boldsymbol {T}\vert \boldsymbol{w}) = \prod_{n=1}^{N}y_n^{t_n}(1-y_n)^{1-t_n}\]베르누이 분포의 형태와 동일함.
예를 들어, 주어진 목표값 벡터가 다음과 같다고 할 때, \(t = (1,0,1)^{T}\)우도함수는
\(\begin{align} p(\boldsymbol{t}\vert \boldsymbol{w}) &= (y_{1}^{1}(1-y_{1})^{0})\times (y_{2}^{0}(1-y_{2})^{1})\times (y_{3}^{1}(1-y_{3})^{0}) \\\\ &= p(\mathcal{C}_{1}\vert \phi_{1})\times p(\mathcal{C}_{2}\vert \phi_{2})\times p(\mathcal{C}_{1}\vert \phi_{3}) \end{align}\)
이 식을 compact하게 표현한 것이 위의 우도함수 식임.
음의 로그 우도 (the negative logarithm of the likelihood)
\[E(\boldsymbol{w})= - \ln{p(\boldsymbol {T}\vert \boldsymbol{w})} = - \sum_{n=1}^{N}\left\{t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\right\}\]Likelihood를 Maximize하는 것이 아니라 음의 로그우도를 minimize하는 식으로 풀게 되는 것임.
\(t_n\)은 타겟값이고 \(y_n\)은 예측한 값임.
\(t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\) 이런식으로 표현된 것이 Cross Entropy Error Function이라고 부름.Cross Entropy는 정보이론(Information Theory)에서 나온 것임.
\(y_n = \sigma(a_n)\), \(a_n = \boldsymbol{w}^T\phi_n\)
이것을 크로스 엔트로피 에러함수(cross entropy error function)라고 부른다.
Cross entropy의 일반적인 정의
\[H(p,q) = - \mathbb{E}_p[\ln q]\]두 개의 확률분포 p,q가 주어졌을 때, 로그 q의 기댓값으로 정의함.
이산확률변수의 경우
\[H(p,q) = - \sum_{x}p(x)\ln q(x)\]두 개의 확률분포가 가까울 수록 Cross entropy가 최소화됨.
일반적으로 Cross entropy가 최소화될 때 두 확률분포의 차이가 최소화된다. 따라서 에러함수 \(E(\boldsymbol{w})\)를 최소화시키는 것을
- 우도를 최대화시키는 것 (우도함수를 최대화 시키다보면 에러함수를 최소화시켜야 한다는 것을 알게됨)
- 모델의 예측값(의 분포)과 목표변수(의 분포)의 차이를 최소화시키는 것
두 가지의 관점에서 이해할 수 있다.
앞에서 최소제곱법이 효과적이지 못했던 이유는, 목표값의 분포가 가우시안을 따르지 않았기 때문임.
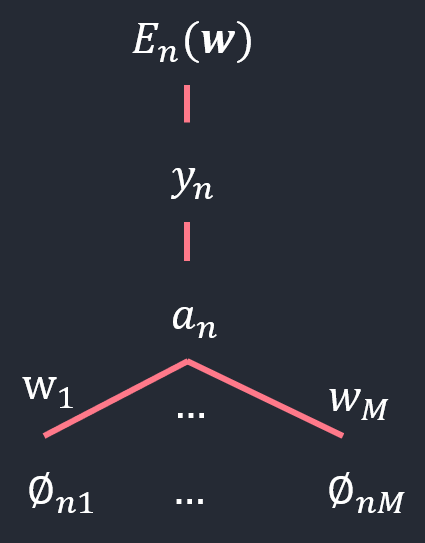
에러함수의 \(\boldsymbol{w}\)에 대한 gradient를 구해보자.
\[E_n(\boldsymbol{w}) = - \left\{t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\right\}\]에러함수(\(\triangledown E(\boldsymbol{w})\))는 모든 데이터에 대한 에러를 합한 것임.
식을 간단하게 하기 위해서 하나의 데이터에 대한 에러를 알아볼 것임.
에러함수가 파라미터 \(\boldsymbol{w}\)와 어떤 관계를 가지고 있는지를 생각해보자.\(y_n = \sigma(a_n)\) \(a_n\)는 파라미터 \(\boldsymbol{w}\)에 대한 선형함수 였음. (음의 로그 우도 참고)
\(a_n = \boldsymbol{w}^T\phi_n\)
\(y_n\), \(a_n\)을 에러식에 대입하면 \(\boldsymbol{w}\)에 관련된 식임을 알 수 있음.도식적으로 표현하면,
함수 \(E_n(\boldsymbol{w})\)를 \(\boldsymbol{w}\)에 관해서 미분을 하려고 할때, chain rule을 쓰면됨.
클래스가 2개인 경우에는 \(\boldsymbol{w}\)와 \(a_n\), \(E_n(\boldsymbol{w})\)사이의 관계가 오직 \(a_n\)과 \(y_n\)을 통해서만 지나가기 때문에,
아래 처럼 chain rule을 쓰면 됨.\(\frac{\partial E_n(\boldsymbol{w})}{\partial y_n}\frac{\partial y_n}{\partial a_n}\triangledown a_n\)를 보면,
먼저, \(\triangledown a_n\): \(a_n\)을 \(\boldsymbol{w}\)에 관해서 미분하고,그 다음, \(\frac{\partial y_n}{\partial a_n}\): \(y_n\)을 \(a_n\)에 관해서 미분
마지막으로, \(\frac{\partial E_n(\boldsymbol{w})}{\partial y_n}\): \(E_n(\boldsymbol{w})\)을 \(y_n\)에 관해서 미분
\(\frac{\partial E_n(\boldsymbol{w})}{\partial y_n}\): \(E_n(\boldsymbol{w}) = - \left\{t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\right\}\)을 \(y_n\)에 미분한 결과는 \(\left\{ \frac{1-t_n}{1-y_n} - \frac{t_n}{y_n}\right\}\) 이렇게 되고,
\(\frac{\partial E_n(\boldsymbol{w})}{\partial y_n}\): \(y_n = \sigma(a_n)\) 으로 로지스틱 시그모이드 함수의 미분은 \(y_n(1-y_n)\) 이런식으로 계산이 됨.
\(\triangledown a_n\): \(a_n = \boldsymbol{w}^T\phi_n\)은 선형식이기 때문에 \(\phi_n\)이 됨.
이 식을 정리하면 아래식의 결과인 \((y_n - t_n)\phi_n\)이 됨.
따라서 전체 에러의 \(\boldsymbol{w}\)에 대한 미분은 \(\triangledown E(\boldsymbol{w}) = \sum_{n=1}^N (y_n - t_n)\phi_n\)임.
라고 정의하면
\[\triangledown E(\boldsymbol{w}) = \sum_{n=1}^N \triangledown E_n(\boldsymbol{w})\] \[\begin{align} \triangledown E_n(\boldsymbol{w}) &\ = \frac{\partial E_n(\boldsymbol{w})}{\partial y_n}\frac{\partial y_n}{\partial a_n}\triangledown a_n\\ &\ = \left\{ \frac{1-t_n}{1-y_n} - \frac{t_n}{y_n}\right\} y_n(1-y_n)\phi_n\\ &\ = (y_n - t_n)\phi_n \end{align}\]따라서
\[\triangledown E(\boldsymbol{w}) = \sum_{n=1}^N (y_n - t_n)\phi_n\]다중클래스 로지스틱 회귀 (Multiclass logistic regression)
\[p(\mathcal{C}_k\vert \phi) = y_k(\phi) = \frac{\exp(a_k)}{\sum_j \exp(a_j)}\] \[a_k = \boldsymbol{w}_k^T \phi\]지수함수를 사용함.
우도함수
2개의 클래스일 때의 우도함수: \(p(\boldsymbol {T}\vert \boldsymbol{w}) = \prod_{n=1}^{N}y_n^{t_n}(1-y_n)^{1-t_n}\)
특성벡터 \(\phi_n\)를 위한 목표벡터 \(\boldsymbol{t}_n\)는 클래스에 해당하는 하나의 원소만 1이고 나머지는 0인 1-of-K 인코딩 방법으로 표현된다.
\[p(\boldsymbol {T}\vert \boldsymbol{w}_1,...\boldsymbol{w}_K) = \prod_{n=1}^{N}\prod_{k=1}^{K} p(\mathcal{C}_k\vert \phi_n)^{t_{nk}} = \prod_{n=1}^{N}\prod_{k=1}^{K}y_{nk}^{t_{nk}}\]실제로 데이터에 클래스 k가 주어져있는지에 따라서 결정이 됨. 클래스의 해당 값이 1이면 하나의 확률값만 남게 됨.
\(T = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}\) (각각의 행이 하나의 데이터)
\(p(\mathcal{C}_{1}\vert \phi_{1}) = 1\)임 첫번째 행의 값 (\(\phi_{1}\)에서의 subscript는 index를 의미함)
\(p(\mathcal{C}_{3}\vert \phi_{2}) = 1\).\(y\)를 사용해서 표현한다면, \(y_{nk}^{t_{nk}\)에서 첫번째 supscript(\(n\))는 데이터 인덱스, 두번째 subscript(\(k\))는 클래스 인덱스
\[p(\boldsymbol {T}\vert \boldsymbol{w}_1,\boldsymbol{w}_2,\boldsymbol{w}_3) = (y_{11}^{1}y_{12}^{0}y_{13}^{0})(y_{21}^{0}y_{22}^{0}y_{23}^{1})\]
\(p(\mathcal{C}_{1}\vert \phi_{1}) = y_{11}\), \(p(\mathcal{C}_{3}\vert \phi_{2}) = y_{23}\)\((y_{11}^{1}y_{12}^{0}y_{13}^{0})(y_{21}^{0}y_{22}^{0}y_{23}^{1})\) 이 부분은 \(\prod_{n=1}^{N}\prod_{k=1}^{K}y_{nk}^{t_{nk}}\) 이 식을 그대로 따라 적은 것임.
위의 행렬에서 보인 것처럼 \(y_{11} = p(\mathcal{C}_{1}\vert \phi_{1})\), \(y_{23} = p(\mathcal{C}_{3}\vert \phi_{2})\)
따라서, \(y_{nk} = p(\mathcal{C}_{k}\vert \phi_{n})\) 임.
\(y_{nk} = y_k(\phi_n)\), \(\boldsymbol {T}\)는 \(t_{nk}\)를 원소로 가지고 있는 크기가 \(N \times K\)인 행렬
\(\boldsymbol {T}\)는 크기가 \(N \times K\)인 행렬임을 기억해야함.
음의 로그 우도
\[E(\boldsymbol{w}_1, ..., \boldsymbol{w}_K) = - \ln p(\boldsymbol {T}\vert \boldsymbol{w}_1, ...,\boldsymbol{w}_K) = - \sum_{n=1}^{N} \sum_{k=1}^{K} t_{nk}\ln(y_{nk})\]구해야할 파라미터 \(\boldsymbol{w}\)의 개수는 k개의 벡터임. 각각의 \(\boldsymbol{w}\)의 벡터들의 최소값을 찾아야 하는데, \(\boldsymbol{w}_j\)에 대한 gradient를 구해서, 최적의 해를 구하고, \(j\)의 값이 1일때부터 k일때까지를 구하면, 최적의 파라미터들을 다 찾는 것이 됨.
\(\boldsymbol{w}_j\)에 대한 gradient를 구한다. 먼저 하나의 샘플 \(\phi_n\)에 대한 에러
\[E_n(\boldsymbol{w}_1,\ldots,\boldsymbol{w}_K) = - \sum_{k=1}^{K} t_{nk}\ln(y_{nk})\]를 정의하면
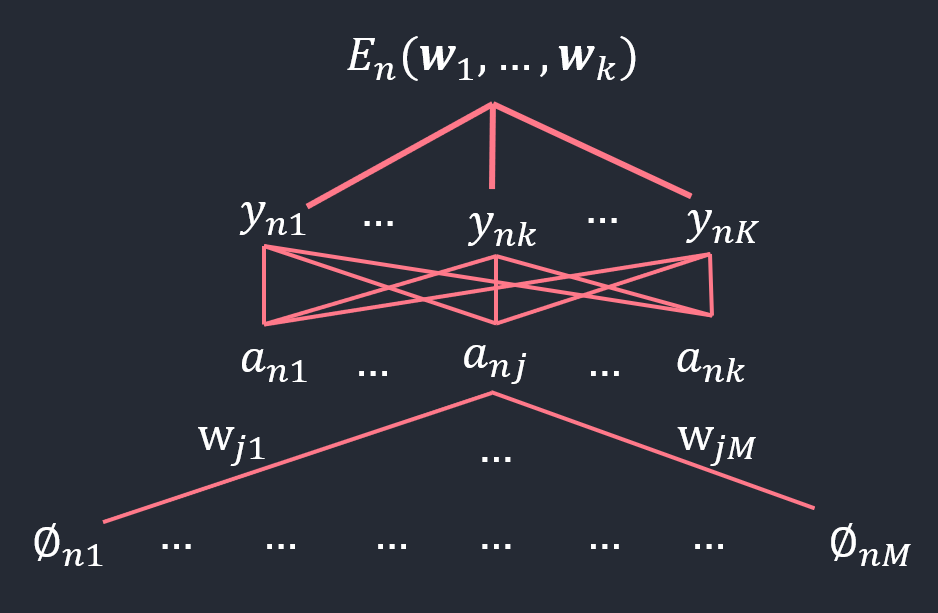
\[\nabla_{ \boldsymbol{w}_j }E(\boldsymbol{w}_1, ...,\boldsymbol{w}_K) = \sum_{n=1}^{N}\nabla_{ \boldsymbol{w}_j }E_n(\boldsymbol{w}_1, ...,\boldsymbol{w}_K)\]다음 함수들 사이의 관계를 주목하라.
- \(E_n\)와 \(\boldsymbol{w}_j\)의 관계는 오직 \(a_{nj}\)에만 의존한다(\(a_{nk}, k\neq j\)는 \(\boldsymbol{w}_j\)의 함수가 아니다).
- \(E_n\)은 \(y_{n1},\ldots,y_{nK}\)의 함수이다.
- \(y_{nk}\)는 \(a_{n1},\ldots,a_{nK}\)의 함수이다.
\[\begin{align} \nabla_{ \boldsymbol{w}_j }E_n &\ = \frac{\partial E_n}{\partial a_{nj}} \frac{\partial a_{nj}}{\partial \boldsymbol{w}_j}\\ &\ = \frac{\partial E_n}{\partial a_{nj}}\phi_n\\ &\ = \sum_{k=1}^K \left( \frac{\partial E_n}{\partial y_{nk}} \frac{\partial y_{nk}}{\partial a_{nj}} \right)\phi_n\\ &\ = \phi_n \sum_{k=1}^K \left\{ - \frac{t_{nk}}{y_{nk}}y_{nk}(I_{kj}-y_{nj}) \right\}\\ &\ = \phi_n \sum_{k=1}^K t_{nk}(y_{nj} - I_{kj})\\ &\ = \phi_n \left( y_{nj}\sum_{k=1}^K t_{nk} - \sum_{k=1}^K t_{nk}I_{kj} \right)\\ &\ = \phi_n (y_{nj} - t_{nj}) \end{align}\]
\(p(\mathcal{C}_k\vert \phi) = y_k(\phi) = \frac{\exp(a_k)}{\sum_j \exp(a_j)}\) 이렇게 소프트 맥스 함수형식으로 표현되어 있는데, 분자에는 \(\exp(a_k)\)가 있는데, 분모에는 모든 \(a\)의 변수들이 더해져 있음. 그래서 \(y_k(\phi) = p(\mathcal{C}_k\vert \phi_n)\)는 단지 \(a_k\)의 관한 함수가 아니라 모든 \(a\)에 관한 함수임.
각각의 \(y_n1 \tilde y_{nk}\)의 변수가 \(a\)와 관련이 있음을 의미함.
그림에서 \(\boldsymbol{w}\)의 차원은 \(M\)임을 기억해야 함.에러함수를 \(\boldsymbol{w}\)로 미분할 때 어떻게 chain rule을 쓸것인가를 결정하기 위해 도식화해봄.
그림에서 보면, \(\boldsymbol{w}_j\)는 반드시 \(\boldsymbol{a}_n\)만을 통과해야 에러함수에 도달이 가능함. \(\boldsymbol{a}_n\)에 도달한 후로는 에러함수로 가기 위해서는 K개의 길이 존재함. 이것이 chain rule을 결정함.
위 식을 전개 👇
\[\frac{\partial E_n}{\partial a_{nj}} \frac{\partial a_{nj}}{\partial \boldsymbol{w}_j}\]
\(E_n\)을 \(\boldsymbol{w}_j\)에 관해서 미분할 것임. \(\boldsymbol{w}_j\)는 \(M\)차원의 벡터임을 잊지말자.\(\boldsymbol{w}_j\)는 \(a_{nj}\)를 통해서만 \(E_n\)에 관계를 가질 수 있음. 따라서 \(a_{nj}\)에 대해서 chain rule을 적용한 것임.
\(\frac{\partial a_{nj}}{\partial \boldsymbol{w}_j}\) = \(\phi_n\)과 같음을 그림에서도 확인함. 왜냐면 \(a_{nj} = \boldsymbol{w}_j^{T}\phi_n\)이기 때문.\(a_{nj}\)와 \(E_n\)의 관계는 \(K\)개의 \(y_n\)변수를 통해서 가기 때문에 이 경로에 대한 합을 다 적어줘야함.(chain rule)
\[\Longrightarrow \sum_{k=1}^K \left( \frac{\partial E_n}{\partial y_{nk}} \frac{\partial y_{nk}}{\partial a_{nj}} \right)\]이렇게 표현할 수 있음.
\(\phi_n\)는 수식앞으로 보내고 나머지 부분을 다시 정리하면,
\[\frac{\partial E_n}{\partial y_{nk}}\]이 부분은 간단함. \(E_n(\boldsymbol{w}_1,\ldots,\boldsymbol{w}_K) = - \sum_{k=1}^{K} t_{nk}\ln(y_{nk})\) 이 식에서 \(y_{nk}\)에 대해서 미분하면 단순히 \(\frac{1}{y_{nk}}\)이 곱해지는 것임.
\[- \frac{t_{nk}}{y_{nk}}\]
따라서,
\[\frac{\partial y_{nk}}{\partial a_{nj}}\]이 부분은 2가지의 경우로 나눠서 생각하면 됨.
(1). \(k\neq j\)
\[\frac{\partial y_{nk}}{\partial a_{nj}}\]이렇게 미분할 때, \(y\)와 \(a\)의 관계는 \(y_k(\phi) = \frac{\exp(a_k)}{\sum_j \exp(a_j)}\) 이런 식의 함수관계임.
\[y_{nk} = \frac{\exp(a_{nk})}{\sum_l \exp(a_{nl})} = \exp(a_{nk})\times \{ \exp(a_{n1})+\ldots+\exp(a_{nl}) \}^{-1}\]
풀어서 써보면 이러한 형태임로 바꿔줄 수 있음(k대신 l을 사용).이제,
\(k\neq j\)인 경우 \(\frac{\partial y_{nk}}{\partial a_{nj}}\) 에서 분자와 분모는 서로 다른 변수임. 분자부분을 미분할 때 상수처럼 취급함.
따라서,
\(\exp(a_{nk})\times \{ \exp(a_n1)+\ldots+\exp(a_{nl}) \}^{-1}\)에서 \(a_nj\)가 나타나는 부분은 분모 \(\{ \exp(a_n1)+\ldots+\exp(a_{nl}) \}^{-1}\)의 하나의 항으로 나타남.미분을 하면,
\[\begin{align} \frac{\partial y_{nk}}{\partial a_{nj}} &= - \frac{\exp(a_{nk})}{\{ \sum_{l}\exp(a_{nl}) \}^2}\exp(a_nj) \\ &= \frac{\exp(a_{nk})}{\sum_{l}\exp(a_{nl})}\times (-\frac{\exp(a_nj)}{\sum_{l}\exp(a_{nl})}) \\ &= y_{nk}\times (- y_{nj}) \end{align}\](2). \(k=j\)
\[\begin{align} \frac{\partial y_{nk}}{\partial a_{nj}} &= \frac{\exp(a_nj)}{\sum_{l}\exp(a_{nl})} - \frac{\exp(a_nj)^2}{\{\sum_{l}\exp(a_{nl})\}^2} \\ &= \frac{\exp(a_nj)}{\sum_{l}\exp(a_{nl})}( 1 - \frac{\exp(a_nj)}{\sum_{l}\exp(a_{nl})} ) \\ &= y_{nk}\times ( 1 - y_{nj}) &\ \mathrm{by}~ y_{nk} = \frac{\exp(a_{nk})}{\sum_l \exp(a_{nl})},\ k=j \implies y_{nk} = y_{nj} \end{align}\]\(y_{nk} = \exp(a_{nk})\times \{ \exp(a_{n1})+\ldots+\exp(a_{nl}) \}^{-1}\) 이기 때문에, 이것을 \(a_{nj}\)에 대해 미분하는데,
두 함수의 곱이 있을 때, 함수 \(f(x)\)와 \(g(x)\)가 곱해져 있을때 그것을 미분을 하면, \(f(x)\)를 미분한 것에 \(g(x)\)를 곱하고 + \(f(x)\)곱하기 \(g(x)\)를 미분한 것으로 계산됨.(Appendix 참조)
따라서, \(f(x)\)인 \(\exp(a_{nk})\)를 \(a_{nj}\)에 대해서 미분하면, \(k=j\)이고 지수함수이기 때문에 \(\exp(a_{nj})\)가 그대로 내려오고(\(f(x)'\)) \(g(x)\)인 \(\{ \exp(a_{n1})+\ldots+\exp(a_{nl}) \}^{-1}\) 을 그대로 곱해주게 되면,
\[\frac{\exp(a_nj)}{\sum_{l}\exp(a_{nl})}\]이 결과가 됨.
\[- \frac{\exp(a_nj)^2}{\{\sum_{l}\exp(a_{nl})\}^2}\]
\(g(x)\)인 \(\{ \exp(a_{n1})+\ldots+\exp(a_{nl}) \}^{-1}\)를 \(a_{nj}\)에 대해서 미분하고, \(f(x) = \exp(a_{nk})\)를 그대로 곱해주면,이 결과가 나옴.
위 의 2가지 경우를 하나의 식으로 나타내면,
\[y_{nk}(I_{kj}-y_{nj})\]단위행렬(\(I_{kj}\))를 사용해서 표현이 가능함. \(\begin{Bmatrix} k\neq j \implies 0 \\ k=j \implies 1 \end{Bmatrix}\)
\[\left\{ - \frac{t_{nk}}{y_{nk}}y_{nk}(I_{kj}-y_{nj}) \right\}\]\[\nabla_{ \boldsymbol{w}_j }E(\boldsymbol{w}_1, ...,\boldsymbol{w}_K) = \sum_{n=1}^{N} (y_{nj}-t_{nj})\phi_n\]이 식을 정리하면 \(t_{nk}(y_{nj}-I_{kj})\) 가 됨.
\(\phi_n \sum_{k=1}^K t_{nk}(y_{nj} - I_{kj})\) 을 풀어서 곱으로 나누어주면 \(\left( y_{nj}\sum_{k=1}^K t_{nk} - \sum_{k=1}^K t_{nk}I_{kj} \right)\) 이 됨.
\(y_{nj}\sum_{k=1}^K t_{nk}\)에서 \(y_{nj}\)는 \(k\)값과 상관없이 때문에 \(\sum\) 밖으로 나옴.
남은 부분인 \(\sum_{k=1}^K t_{nk}\)은 하나의 데이터데 대해서 그때의 타겟 벡터의 원소들을 다 합한 것과 같고 이 값은 결국 1임 (목표값은 하나의 데이터에 대해 반드시 1개의 클래스만 1이 될 수 있기 때문에).
\(\sum_{k=1}^K t_{nk}I_{kj}\) 이 경우도, 결국 \(j\)번째 원소만 남고 나머지는 전부 0이 되기 때문에 \(t_{nj}\)만 남게 됨.최종적으로 하나의 데이터 기저함수를 사용한 \(\phi_n\)에 대해서 에러를 구해서, 그 에러에 \(\boldsymbol{w}_j\)에 대한 gradient(\(\nabla\))는 \(\phi_n (y_{nj} - t_{nj})\)가 되는 것임.
과정은 복잡했지만, 결과로 나온 gradient는 생각보다 단순한 형태..
\(\phi_n (y_{nj} - t_{nj})\): \(\phi_n\)은 입력벡터이고, 예측값(\(y_{nj}\))과 타겟값(\(t_{nj}\))의 차이를 곱해서 이루어지게 됨.
행렬로 표현하면, 더 간단하게 표현이 가능함.
\(\Phi^{T}(\boldsymbol{y}-\boldsymbol{t})\): \(\Phi\)는 Design Matrix
\(\Phi^{T} = \begin{bmatrix} \vert \ \ \\ \boldsymbol{\phi}_{1} \cdots\\ \vert \ \ \end{bmatrix}\)
\(\Phi^{T}\)라는 열벡터로 표현된 행렬에 벡터 \((\boldsymbol{y}-\boldsymbol{t})\)를 곱하는 형태임.위의 합의 형태를 행렬로 간단하게 표현이 가능함.
실습
Gradient Descent (batch)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
import seaborn as sns
X, t = make_classification(n_samples=500, n_features=2, n_redundant=0, n_informative=1,
n_clusters_per_class=1, random_state=14)
t = t[:,np.newaxis]
sns.set_style('white')
sns.scatterplot(X[:,0],X[:,1],hue=t.reshape(-1));
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def compute_cost(X, t, w):
N = len(t)
h = sigmoid(X @ w)
epsilon = 1e-5
cost = (1/N)*(((-t).T @ np.log(h + epsilon))-((1-t).T @ np.log(1-h + epsilon)))
return cost
compute cost
\(E(\boldsymbol{w})= - \ln{p(\boldsymbol {T}\vert \boldsymbol{w})} = - \sum_{n=1}^{N}\left\{t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\right\}\)와 동일한 함수임.
코드에서는 \(\frac{1}{N}\)을 곱하는 형태로 적용한 것임.
\(\frac{1}{N}\)을 곱하는 것이 numerical하게 안정적임. N값이 크게 되면 gradient가 크기 때문에 gradient값이 한꺼번에 많이 움직이는 상황이 발생하기 때문. \(\frac{1}{N}\) 해주면 안정적으로 optimization이 가능함.
h = sigmoid(X @ w): h는 벡터임 broadcasting 되면서, 시그모이드 함수에 들어가는 벡터의 각각의 원소에 대해서 대응하는 로지스틱 시그모이드 함수 값을 원소로 가지게 됨.
epsilon = 1e-5: 로그 값은 안정적으로 구하기 위해서 더해줌.
\(y_{n}\)이 코드에서는h + epsilon인 것임.
def gradient_descent(X, t, w, learning_rate, iterations):
N = len(t)
cost_history = np.zeros((iterations,1))
for i in range(iterations):
w = w - (learning_rate/N) * (X.T @ (sigmoid(X @ w) - t))
cost_history[i] = compute_cost(X, t, w)
return (cost_history, w)
파라미터 w = w -
learning_rate*gradient 임.
앞에서 \(\boldsymbol{x}\)라는 원래의 인풋을 쓰기도 했고 기저함수 \(\phi\)를 쓰기도 했지만, 위 코드에서는 기저함수를 통과하지 않은 원래의 \(\boldsymbol{x}\)를 사용했음.
이 \(\boldsymbol{x}\)도 Design Matrix라고 부를 수 있음.gradient 식과 비교해봄. gradient
\(\triangledown E(\boldsymbol{w}) = \sum_{n=1}^N (y_n - t_n)\phi_n = \Phi^{T}(\boldsymbol{y}-\boldsymbol{t})\): \(\Phi\)는 Design Matrix
\(\Phi^{T} = \begin{bmatrix} \vert \ \ \\ \boldsymbol{\phi}_{1} \cdots\\ \vert \ \ \end{bmatrix}\)
여기선 Design Matrix가 \(\boldsymbol{x}\) 이기 때문에, \(\boldsymbol{x}^{T}\times\) (sigmoid(X @ w)= \(\boldsymbol{y}\))-\(\boldsymbol{t}\) 의 형태가 되는 것임.
def predict(X, w):
return np.round(sigmoid(X @ w))
0 or 1로 출력하도록 만들어줌.
N = len(t)
X = np.hstack((np.ones((N,1)),X))
M = np.size(X,1)
w = np.zeros((M,1))
iterations = 1000
learning_rate = 0.01
initial_cost = compute_cost(X, t, w)
print("Initial Cost is: {} \n".format(initial_cost))
(cost_history, w_optimal) = gradient_descent(X, t, w, learning_rate, iterations)
print("Optimal Parameters are: \n", w_optimal, "\n")
plt.figure()
sns.set_style('white')
plt.plot(range(len(cost_history)), cost_history, 'r')
plt.title("Convergence Graph of Cost Function")
plt.xlabel("Number of Iterations")
plt.ylabel("Cost")
plt.show()
Dummy input을 사용하기 위해
X = np.hstack((np.ones((N,1)),X))1을 열로 하나 추가한 것임.Dummy input을 사용하는 이유?
(cost_history, w_optimal) = gradient_descent(X, t, w, learning_rate, iterations)
여기서 전체 데이터 (X)를 한꺼번에 gradient를 업데이트를 하는 것이기 때문에 batch 업데이트라고 부름.
딥러닝에서 주로 사용하는 batch는 사실 mini-batch를 줄여서 하는 말임.
여기서는 전체 데이터를 다 사용해서 업데이트 한다는 의미임.
(cost_history, w_optimal)
여기서 optimal은 진짜 optimal이 아니라 최종적으로 얻어지는 \(\boldsymbol{W}\)임 (충분히 학습하면 최종적으로 나오는 \(\boldsymbol{W}\)가 optimal이라는 가정하에 붙인 것임)
Accuracy
y_pred = predict(X, w_optimal)
score = float(sum(y_pred == t))/ float(len(t))
print(score)
Draw a decision boundary
slope = -(w_optimal[1] / w_optimal[2])
intercept = -(w[0] / w_optimal[2])
sns.set_style('white')
sns.scatterplot(X[:,1],X[:,2],hue=t.reshape(-1));
ax = plt.gca()
ax.autoscale(False)
x_vals = np.array(ax.get_xlim())
y_vals = intercept + (slope * x_vals)
plt.plot(x_vals, y_vals, c="k");
Stochastic Gradient Descent
파라미터를 업데이트 할때 데이터 전체를 사용하는 것이 아니라 데이터 하나 만을 사용하는 방법.
def sgd(X, t, w, learning_rate, iterations):
N = len(t)
cost_history = np.zeros((iterations,1))
for i in range(iterations):
i = i % N # 처음 위치로
w = w - learning_rate * (X[i, np.newaxis].T * (sigmoid(X[i] @ w) - t[i]))
cost_history[i] = compute_cost(X[i], t[i], w)
return (cost_history, w)
batch(전체):
w = w - (learning_rate/N) * (X.T @ (sigmoid(X @ w) - t))
sgd:w = w - learning_rate * (X[i, np.newaxis].T * (sigmoid(X[i] @ w) - t[i]))
i-th 데이터만 사용해서 업데이트
batch로 했을 때는iterations = 1000으로 전체 데이터를 1000번 읽은 효과
sgd에서iterations = 1000으로 하면, 읽은 샘플의 개수가 1000개인 것임.
X, t = make_classification(n_samples=500, n_features=2, n_redundant=0, n_informative=1,
n_clusters_per_class=1, random_state=14)
t = t[:,np.newaxis]
N = len(t)
X = np.hstack((np.ones((N,1)),X))
M = np.size(X,1)
w = np.zeros((M,1))
iterations = 2000
learning_rate = 0.01
initial_cost = compute_cost(X, t, w)
print("Initial Cost is: {} \n".format(initial_cost))
(cost_history, w_optimal) = sgd(X, t, w, learning_rate, iterations)
print("Optimal Parameters are: \n", w_optimal, "\n")
plt.figure()
sns.set_style('white')
plt.plot(range(len(cost_history)), cost_history, 'r')
plt.title("Convergence Graph of Cost Function")
plt.xlabel("Number of Iterations")
plt.ylabel("Cost")
plt.show()
Accuracy
y_pred = predict(X, w_optimal)
score = float(sum(y_pred == t))/ float(len(t))
print(score)
Mini-batch Gradient Descent
배치 사이즈를 조절해서 함.
def batch_gd(X, t, w, learning_rate, iterations, batch_size):
N = len(t)
cost_history = np.zeros((iterations,1))
shuffled_indices = np.random.permutation(N)
X_shuffled = X[shuffled_indices]
t_shuffled = t[shuffled_indices]
for i in range(iterations):
i = i % N # 태초마을
X_batch = X_shuffled[i:i+batch_size]
t_batch = t_shuffled[i:i+batch_size]
# batch가 epoch 경계를 넘어가는 경우, 앞 부분으로 채워줌
if X_batch.shape[0] < batch_size:
X_batch = np.vstack((X_batch, X_shuffled[:(batch_size - X_batch.shape[0])]))
t_batch = np.vstack((t_batch, t_shuffled[:(batch_size - t_batch.shape[0])]))
w = w - (learning_rate/batch_size) * (X_batch.T @ (sigmoid(X_batch @ w) - t_batch))
cost_history[i] = compute_cost(X_batch, t_batch, w)
return (cost_history, w)
데이터를 shuffle 해줌.(배치 사이즈 만큼 읽기 때문에 특정 batch에서의 영향을 줄이기 위해)
if X_batch.shape[0] < batch_size:이것은 pytorch에서dataloader(droplast=True)로 사용하면 에러없이 가능함.
X, t = make_classification(n_samples=500, n_features=2, n_redundant=0, n_informative=1,
n_clusters_per_class=1, random_state=14)
t = t[:,np.newaxis]
N = len(t)
X = np.hstack((np.ones((N,1)),X))
M = np.size(X,1)
w = np.zeros((M,1))
iterations = 1000
learning_rate = 0.01
initial_cost = compute_cost(X, t, w)
print("Initial Cost is: {} \n".format(initial_cost))
(cost_history, w_optimal) = batch_gd(X, t, w, learning_rate, iterations, 32)
print("Optimal Parameters are: \n", w_optimal, "\n")
plt.figure()
sns.set_style('white')
plt.plot(range(len(cost_history)), cost_history, 'r')
plt.title("Convergence Graph of Cost Function")
plt.xlabel("Number of Iterations")
plt.ylabel("Cost")
plt.show()
Accuracy
y_pred = predict(X, w_optimal)
score = float(sum(y_pred == t))/ float(len(t))
print(score)
딥러닝에서는 mini-batch를 보통사용함.
SGD 같은 경우 민감하게 반응하기 때문에.
Appendix
Derivative of the product of two functions
\(f(x) = g(x)h(x) \Rightarrow f'(x)=g'(x)h(x)+g(x)h'(x)\)
MathJax
left align:
\[\begin{align} &\ A = AAAA \\ &\ AAAAA = A \\ &\ AAA = AA \end{align}\]$$\begin{align} &\ A = AAAA \\ &\ A = A \\ &\ A = AA \end{align}$$
escape unordered list
- \(cov[\boldsymbol{x}_{a}] = \Sigma_{aa}\):
\- $$cov[\boldsymbol{x}_{a}] = \Sigma_{aa}$$
\setminus
\(\{A\}\setminus\{B\}\):
$$\{A\}\setminus\{B\}$$
adjustable parenthesis
\(\left( content \right)\):
$$\left( content \right)$$
Matrix with parenthesis \(\pmatrix{a_{11} & a_{12} & \ldots & a_{1n} \cr a_{21} & a_{22} & \ldots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{m1} & a_{m2} & \ldots & a_{mn} }\):
$$\pmatrix{a_{11} & a_{12} & \ldots & a_{1n} \cr a_{21} & a_{22} & \ldots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{m1} & a_{m2} & \ldots & a_{mn} }$$
References
Pattern Recognition and Machine Learning: https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
Sigmoid & Logistics function: https://stats.stackexchange.com/questions/204484/what-are-the-differences-between-logistic-function-and-sigmoid-function/204485
Generalized Linear Model and Logistic: https://sebastianraschka.com/faq/docs/logistic_regression_linear.html

Leave a comment