NN basics - MLP

June 30, 2021 5 minute read

퍼셉트론

퍼셉트론의 동작

내적에 의한 선형과 활성함수에 의한 비선형에 의해 의미를 구분.
결국엔 공간의 분할을 만든다.
선형대수에서 w라는 가중치에 input을 내적하고 w에 projection했을때, 그 값이 0이면 직교하는 것이고, 0을 기준으로 비선형적 요소로 +1, -1로 출력값을 만드는 것임.

임계값을 원점으로 옮겨오기위해 bias term 추가함.

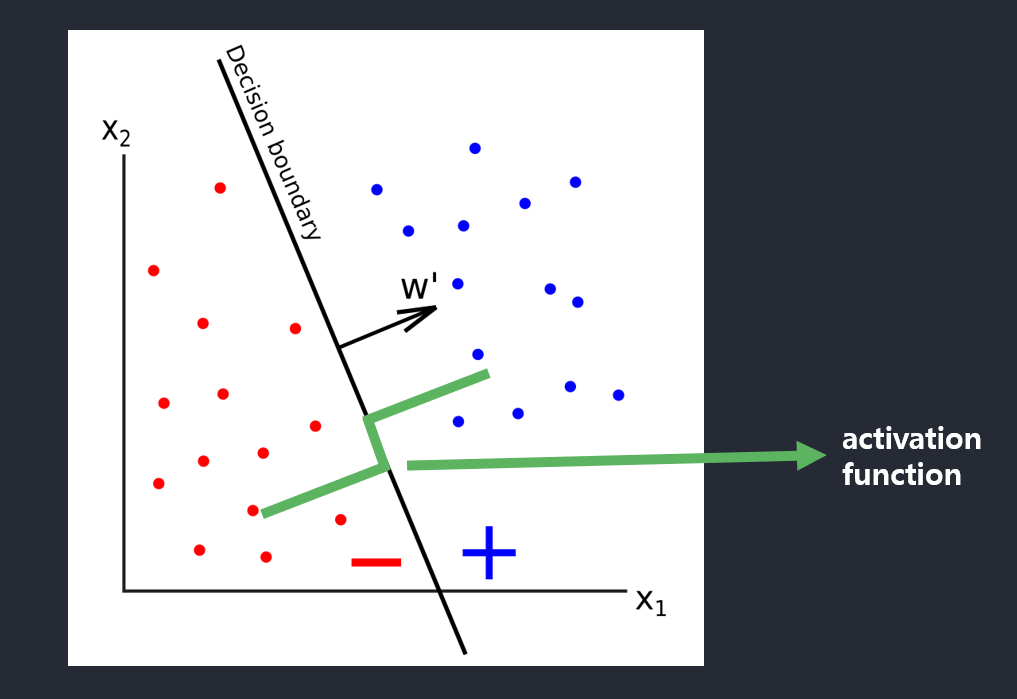
기하학적으로 설명

결정 직선 \(d(\boldsymbol{x}) = d(x_1,x_2) = w_{1}x_{1} + w_{2}x_{2} + w_{0} = 0 \rightarrow x_{1}+x_{2} - 0.5 = 0\)
- \(w_{1}\)과 \(w_{2}\)는 직선의 기울기, \(w_{0}\)는 절편(intercept)(편향)을 결정
- 결정 직선은 특징 공간을 +1과 -1의 두 부분공간으로 이분할 하는 분류기 역할
\(d\)차원 공간으로 일반화 \(d(\boldsymbol{x}) = d(x_1,x_2) = w_{1}x_{1} + \ldots + w_{d}x_{d} + w_{0} = 0\)
- 2차원: 결정 직선(decision line), 3차원: 결정 평면(decision plane), 4차원이상: 결정 초평면(decision hyperplane)

퍼셉트론의 학습

목적함수 정의 (손실함수)

목적함수의 상세 조건

\(\boldsymbol{J(w)} \ge 0\) 이다.
\(\boldsymbol{w}\)가 최적이면(모든 샘플을 맞히면), \(\boldsymbol{J(w)} = 0\).
틀리는 샘플이 많은 \(\boldsymbol{w}\)일 수록 \(\boldsymbol{J(w)}\)는 큰 값을 가진다.

목적함수 상세 설계

\(J(\boldsymbol{w}) = \sum_{\boldsymbol{x}_{J}\in Y} - y_{k}(\boldsymbol{w}^{T}\boldsymbol{x}_{k})\).
- 임의의 샘플 \(\boldsymbol{x}_{k}\)가 \(Y\)에 속한다면(오분류 시), 퍼셉트론의 예측 값(+1 or -1) \(\boldsymbol{w}^{T}\boldsymbol{x}_{k}\)와 실제 값 \(\boldsymbol{y}_{k}\)는 부호가 다름(+1을 -1로 예측) \(\rightarrow - y_{k}(\boldsymbol{w}^{T}\boldsymbol{x}_{k})\)는 항상 양수를 가짐
  - 예측값의 부호가 다르기 때문에 \(- y_{k}(\boldsymbol{w}^{T}\boldsymbol{x}_{k})\)는 항상 양수임(실제값:\(y_{k}\), 예측값:\((\boldsymbol{w}^{T}\boldsymbol{x}_{k})\))
- 결국 \(Y\)가 클수록(틀린샘플이 많을 수록), \(J(\boldsymbol{w})\)는 큰 값을 가짐
- \(Y\)가 공집합일 때 (즉, 퍼셉트론이 모든 샘플을 맞출 때), \(J(\boldsymbol{w}) = 0\) 임.

경사 하강법 (Gradient Descent)

최소 \(J(\Theta)\) 기울기를 이용하여 반복탐색하여 극값을 찾음

gradient는 커지는 방향(음수)이기 때문에 마이너슬 붙여서 작아지는 방향으로 이동시킴.

\[\Theta_{t} - \rho g,\ g = \frac{\partial J(\Theta)}{\partial \Theta}\]

Rho(\(\rho\)) is the rate at which the price of a derivative changes relative to a change in the risk-free rate of interest.

경사도 계산
- 일반화된 가중치 갱신 규칙 \(\Theta = \Theta -\rho\boldsymbol{g}\)를 적용하려면 경사도 \(\boldsymbol{g}\)가 필요함.
- \(J(\boldsymbol{w}) = \sum_{\boldsymbol{x}_{J}\in Y} - y_{k}(\boldsymbol{w}^{T}\boldsymbol{x}_{k})\)을 편미분하면
- \[\frac{\partial J(\boldsymbol{w})}{\partial w_{j}} = \sum_{x_{k}\in Y} \frac{\partial (-y_{k} ( w_{0}x_{k0} + w_{1}x_{k1} + \ldots + w_{i}x_{ki} + \ldots + + w_{d}x_{kd} ) )}{\partial w_{i}} = \sum_{x_{k}\in Y} -y_{k}x_{ki}\]
  - 미분하고자 하는 \(w_{i}\)를 제외하고 나머지 상수취급
  - 결국 \(y_{k}\ x_{ki}\) 만 남게됨
- 결국 \(w_{i}\)를 \(1 \sim d\) 까지 하는 것임.
델타규칙
- 편미분 결과인 \(\sum_{x_{k}\in Y} -y_{k}x_{ki}\)을 \(\Theta = \Theta -\rho\boldsymbol{g}\)에 대입.
- \(w_{i} = w_{i} + \rho\sum_{x_{k}\in Y} y_{k}x_{ki} (i = 0,1,\ldots,d)\).
- 벡터 형태로 확장이 가능함.
- 퍼셉트론의 학습방법

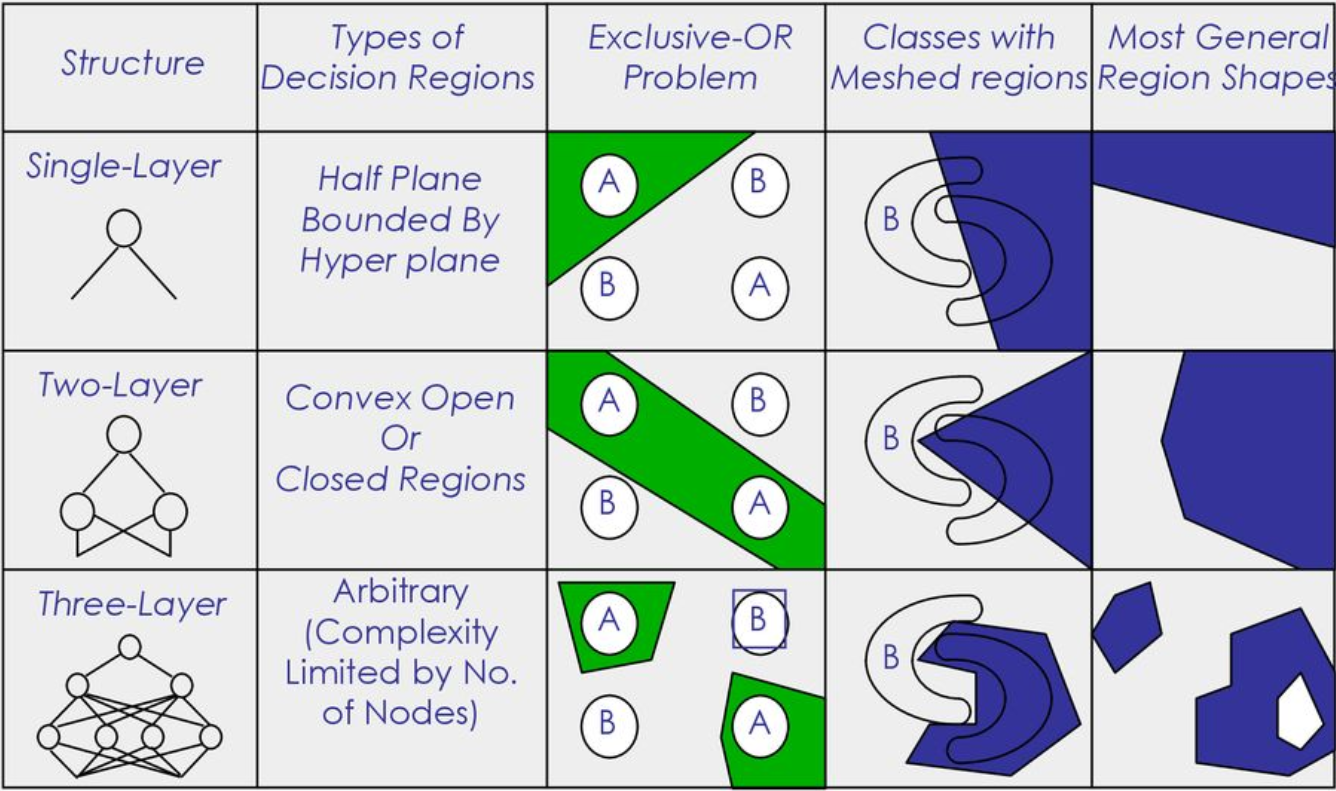
다층 퍼셉트론

퍼셉트론은 선형 분류기라는 한계를 가짐.

핵심 아이디어

은닉층: 은닉층은 원래 특징 공간을 분류하는 데 훨씬 유리한 새로운 특징 공간으로 변환함.
시그모이드 활성함수: 퍼셉트론은 계단함수(+1, -1)를 활성함수로 사용함. 반면, 다층 퍼셉트론은 시그모이드함수를 활성함수(continuous)로 사용함. 연속값으로 출력을 함.
오류 역전파 알고리즘: 다층 퍼셉트론은 여러 층이 순차적으로 이어진 구조이므로, 역방향으로 진행하면서 한 번에 한 층씩 Gradient를 계산하고 Weight를 갱신하는 방식.

특징 공간 변환(은닉층)

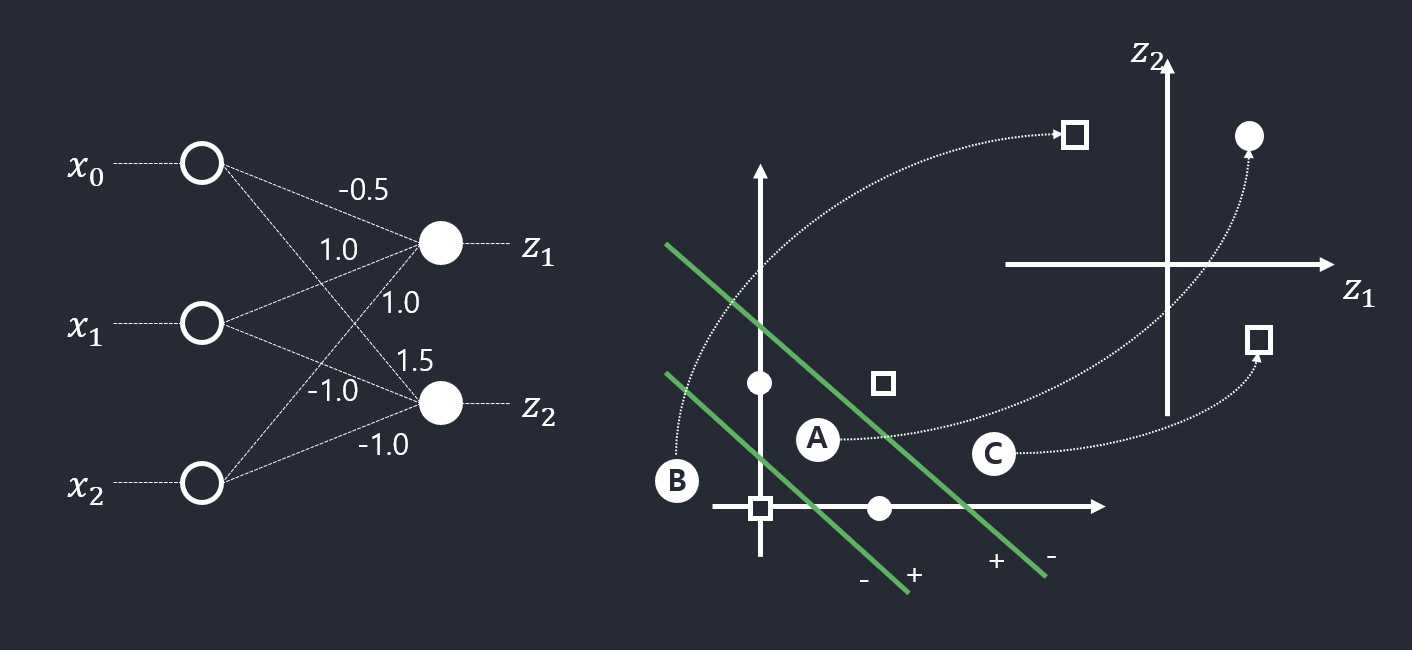
퍼셉트론 2개를 병렬로 결합하면
- 원 공간 \(\boldsymbol{x} = (x_1, x_2)^{T}\)를 새로운 특징 공간 \(\boldsymbol{z} = (z_1, z_2)^{T}\)로 변환
- 새로운 특징 공간 \(\boldsymbol{z}\)에서는 선형 분리가 가능함.
다층 퍼셉트론의 용량
- 3개 퍼셉트론을 결합하면, 2차원 공간을 7개 영역으로 나누고 각 영역을 3차원 점으로 변환
- 활성함수 \(\tau\)로 계단함수를 사용하므로 영역을 점으로 변환
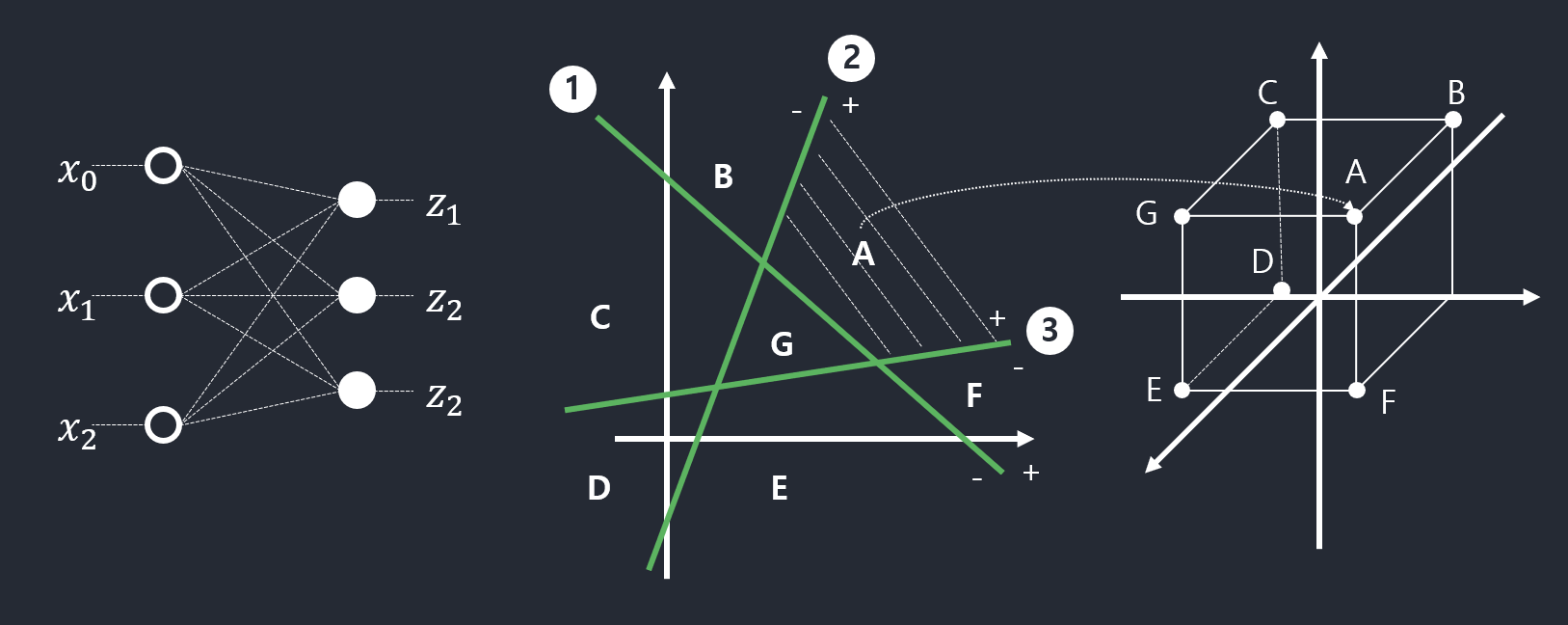
- 일반화하여, \(p\)개의 퍼셉트론을 결합하면 \(p\)차원 공간으로 변환
  - \(1+\sum_{i=1}^{p}i\)개의 영역으로 분할

활성함수

로지스틱 시그모이드
- range: \(\left[ 0,1 \right]\)
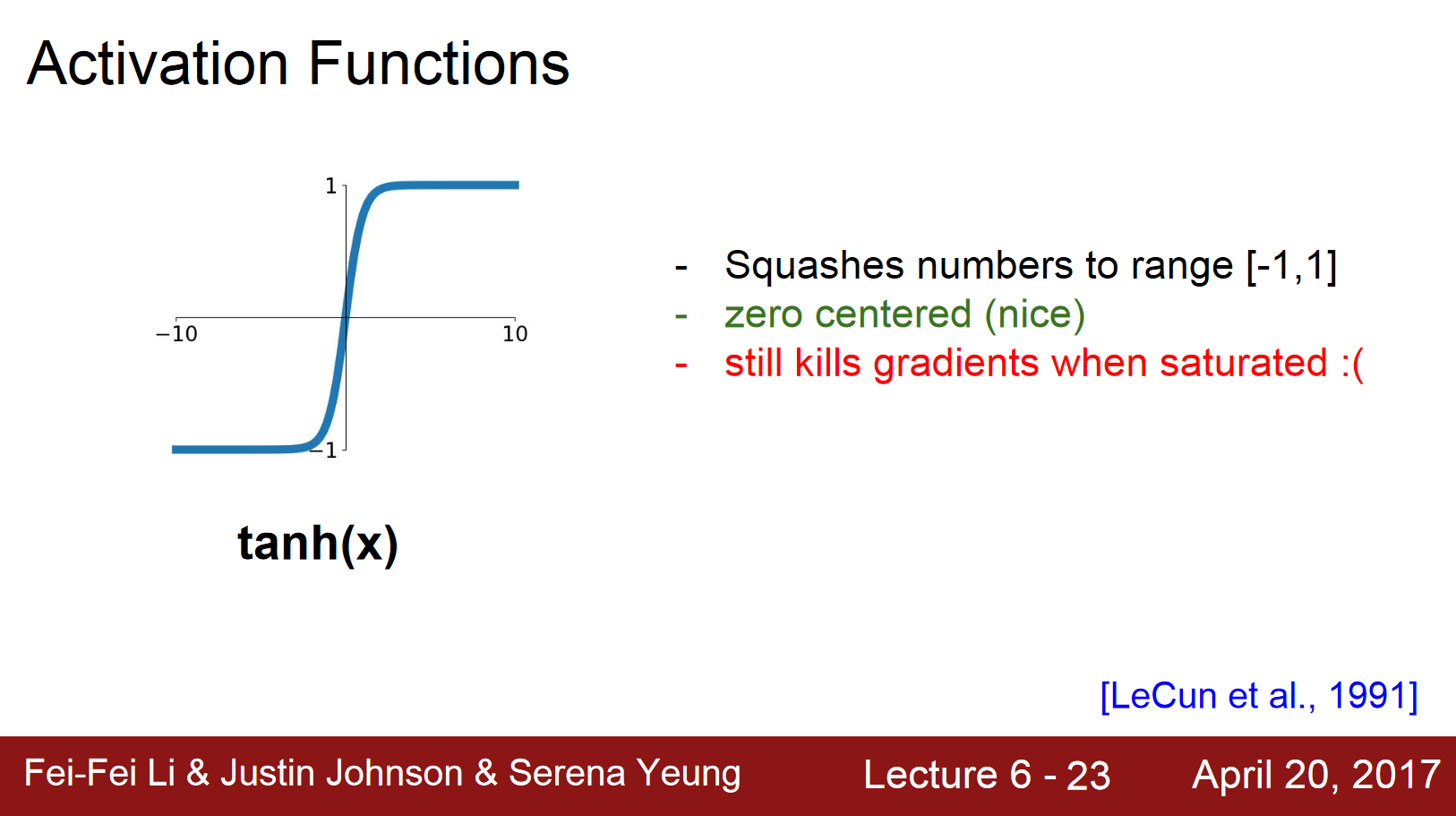
하이퍼볼릭 탄젠트 시그모이드
- range: \(\left[ -1,1 \right]\)
softplus와 rectifier
- range: \(\left[ 0,\infty \right]\)
- SoftPlus is a smooth approximation to the ReLU function
- rectifier: input 값이 0보다 작은 경우 0으로 inactivate되어있다가 0보다 큰 값이 들어오면 activate됨.
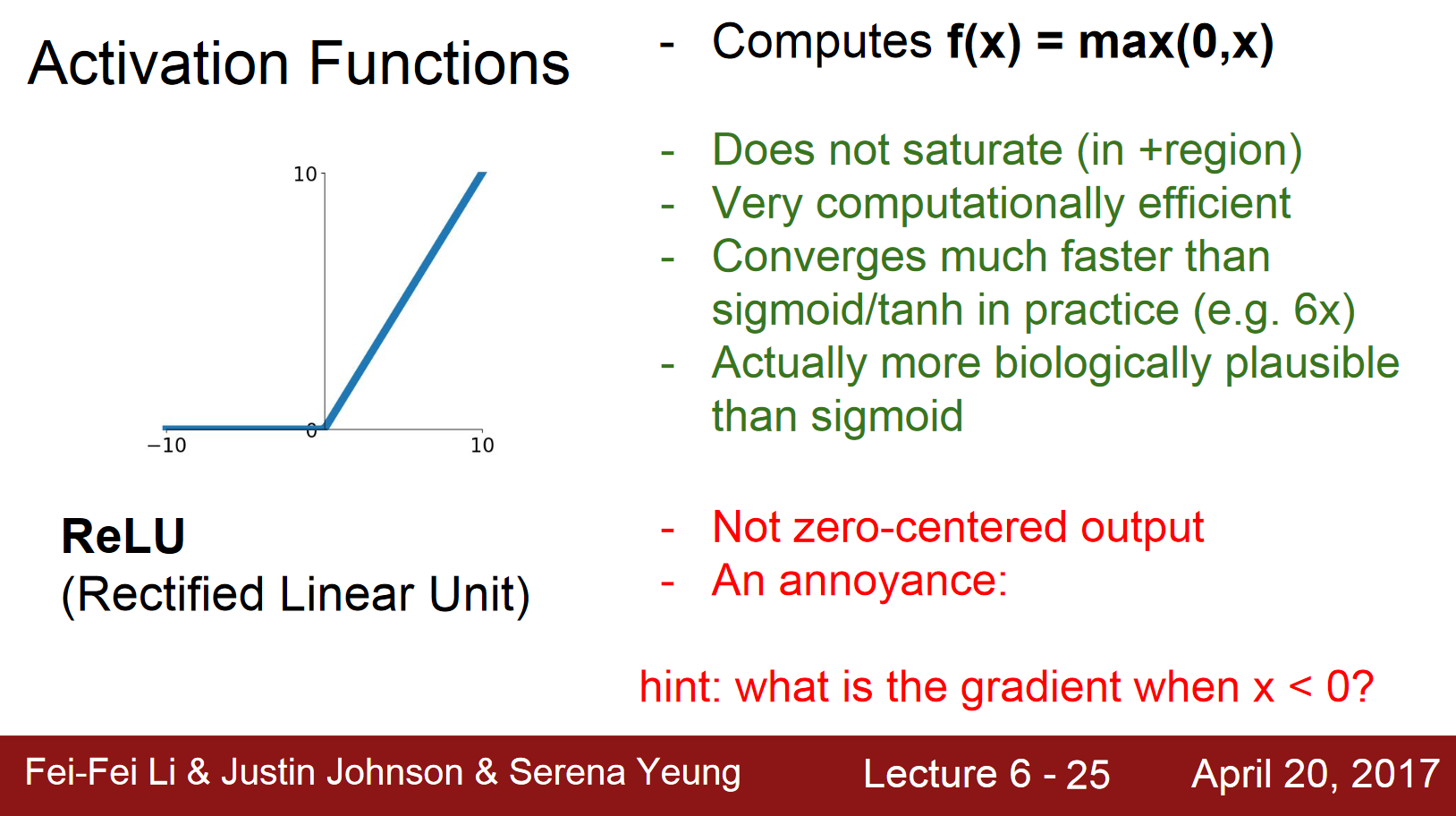
Activation Functions & Gradient of those
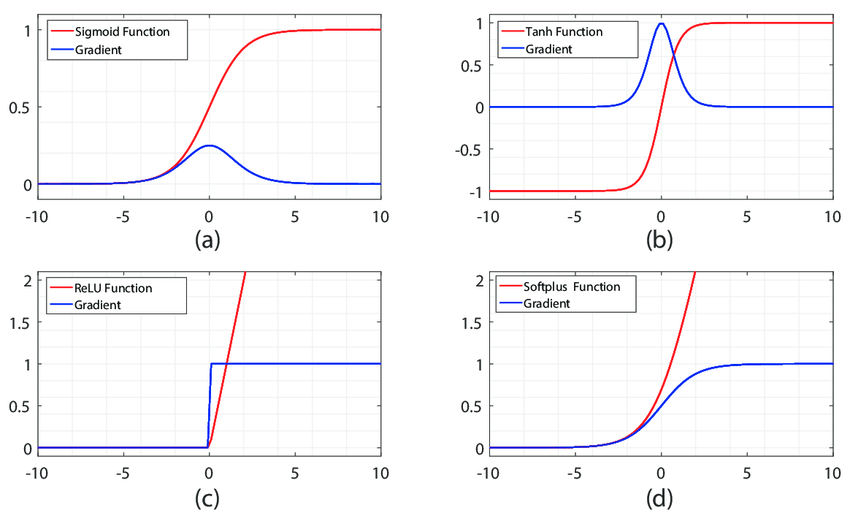
- sigmoid and tanh activation functions’ gradient becomes zero.

은닉층은 특징 추출기

은닉층이 가지고 있는 학습을 통해 결정되는 가중치에 따라 입력값의 특징들이 부각되는 것임.
앞에서 뽑힌 특징들을 점진적으로 학습하는 것임.
보다 특징들이 추상화 되는 것임.

은닉층의 깊이에 따른 이점
- 지수의 표현
  - 깊이가 깊어질 수록 의미가 더 두드러지는 공간의 변화를 만들것 임.
  - 그 공간은 생각보다 심플하게 나뉘어질 수 있음.
  - 각 은닉층은 입력 공간을 어디서 접을지 지정 –> 지수적으로 많은 선형적인 영영 조각들의 조합으로 표현됨.
- 성능 향상

오류 역전파 알고리즘

순방향 전파로 \(w_1, w_2\)를 통해서 나온 예측값과 실제값의 차이를 줄이기 위해 각각의 \(w_1, w_2\)를 경사하강법을 취해 목적함수 \(\boldsymbol{J}(w)\)를 가중치로 편미분하여 최소화한다.
즉 \(w_2\)에서 들어오는 오차가 \(w_1\)에 영향을 미치게 되는데 이게 back propagation이다.
역전파 방법은 결과 값을 통해서 다시 역으로 input 방향으로 오차를 다시 보내며 가중치를 재업데이트 하는 것이다. 물론 결과에 영향을 많이 미친 노드(뉴런)에 더 많은 오차를 돌려줄 것이다.

목적함수의 정의

훈련집합
- 특징 벡터 집합 \(X\), \(Y\)
- 분류 벡터는 one-hot코드로 표현됨. 즉 \(y_i = (0,0,...,1,...,0)^T\)
기계학습의 목표
- 모든 샘플을 옳게 분류하는 함수 f를 찾는 일
목적함수
- 가장 많이 쓰이는 평균 제곱 오차(MSE)
  - L2 norm 사용
  - 온라인 모드 : 배치모드를 스트리밍으로 하는 것.
  - 배치 모드 : 데이터셋을 특정 단위 n개만큼 보는 것.

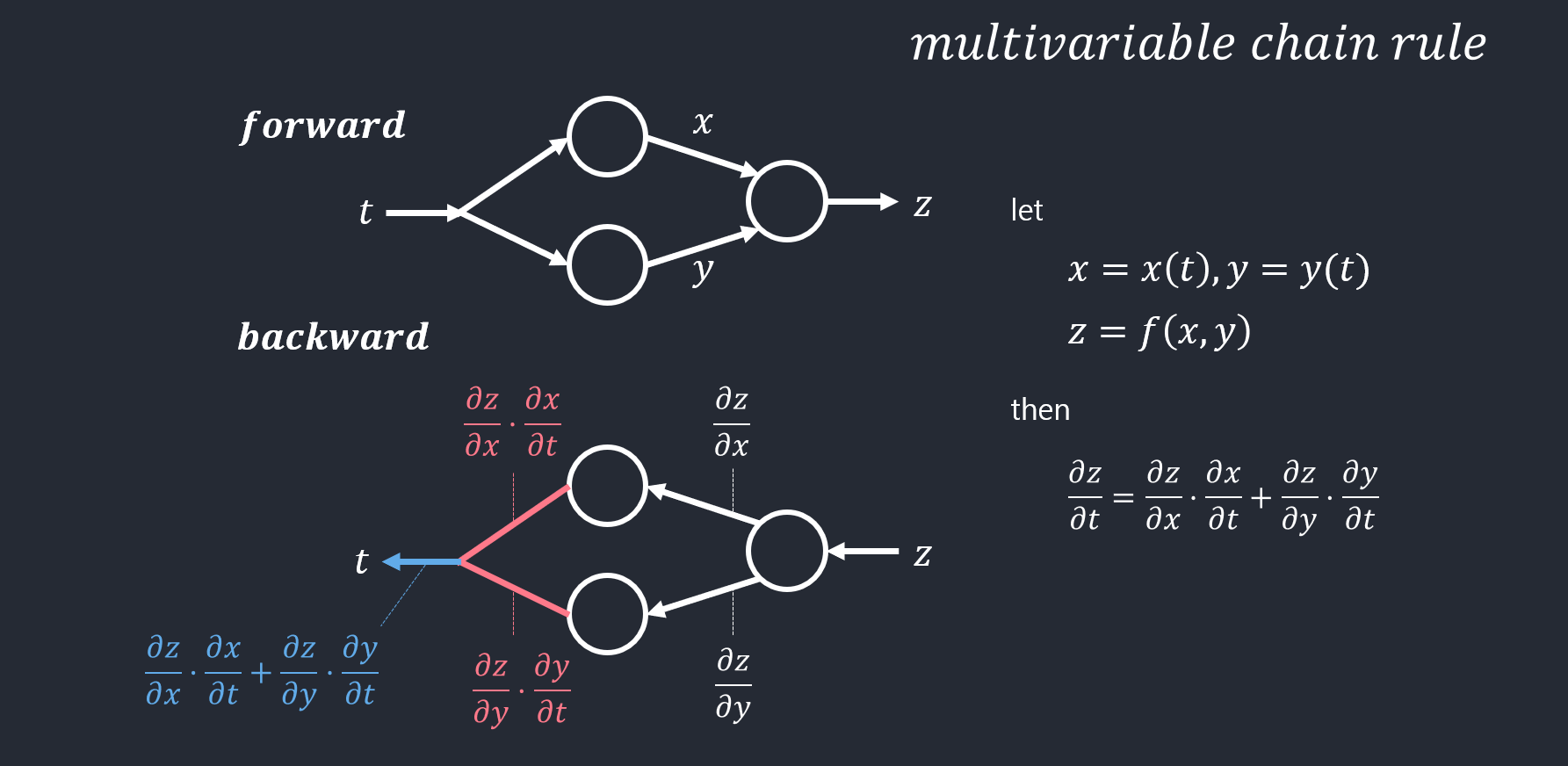
오류 역전파를 이용한 학습 알고리즘

연산그래프(전방 연산을 그래프로 표현할 수 있음)
연쇄 법칙(chain rule)의 구현
- 반복되는 부분식들을 저장하거나 재연산을 최소화(예: 동적 프로그래밍)
- 그래디언트를 구할 때 신경망에서 연속해서 일어나는 연쇄법칙을 오류역전파할때 활용한다.
- \({\partial E \above 1pt \partial w_{ij}} = {\partial E \above 1pt \partial o_j}{\partial o_j \above 1pt \partial net_j}{\partial net_j \above 1pt \partial w_ij}\).
- 체인룰(연쇄법칙)을 통해 끝에서부터 나오는 오류(손실함수)를 내가 원하는 위치까지 보낼 수 있다.
목적함수를 다시 쓰면, \(J(\Theta) = {1 \above 1pt 2}\left \| y - o(\Theta) \right \|_{2}^{2}\)(2층 퍼셉트론의 경우 \(\Theta = {\boldsymbol{U}^1, \boldsymbol{U}^2}\))
이 목적함수의 최저점을 찾아주는 경사하강법(2층 퍼셉트론의 경우)
- \(\boldsymbol{U}^1 = \boldsymbol{U}^1 - \rho \frac{\partial J}{\partial \boldsymbol{U}^1}\).
- \(\boldsymbol{U}^2 = \boldsymbol{U}^2 - \rho \frac{\partial J}{\partial \boldsymbol{U}^2}\).
- \(X -> \boldsymbol{U}^1_ -> \boldsymbol{U}^2 -> J(\Theta)\)으로 연산이 순차적으로 진행된다.
- 이걸 역으로 미분하여 체인룰을 통해 오류역전파를 사용하여 내가 원하는 위치의 것을 활용할 수 있다.
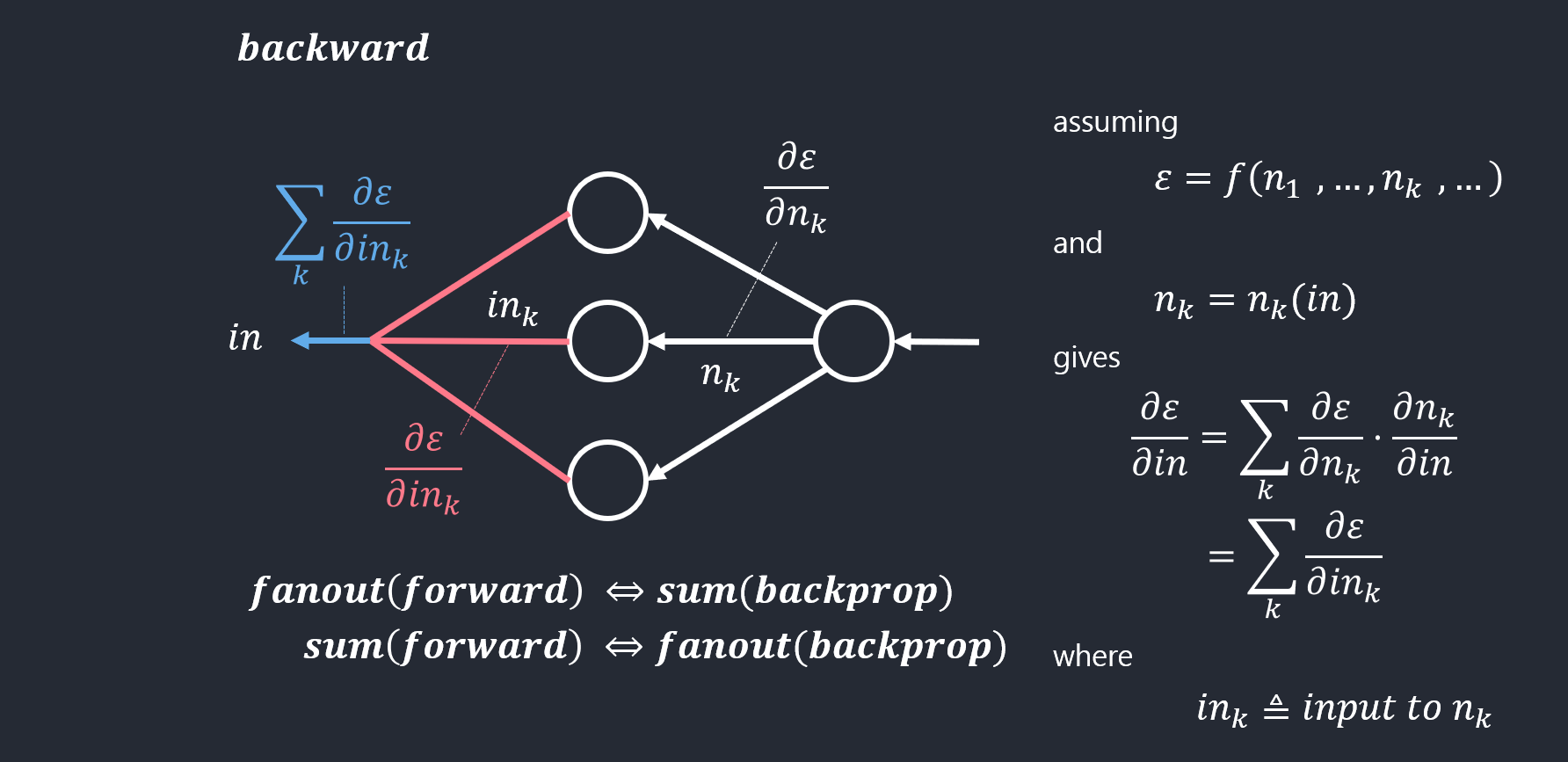
오류 역전파 알고리즘
- 출력의 오류를 역방향(오른쪽에서 왼쪽으로)으로 전파하며 경사도를 계산하는 알고리즘
- 반복되는 부분식들의 경사도의 지수적 폭발(exponential explosion) 혹은 사라짐(vanishing)을 피해야함.
[경사도 단순화] 역전파 분해(backprop with scalars)
- x, y, z가 서로 스칼라라고 하자. 두 입력이 들어와서 처리를 해서 내보내는 것을 생각해보자.
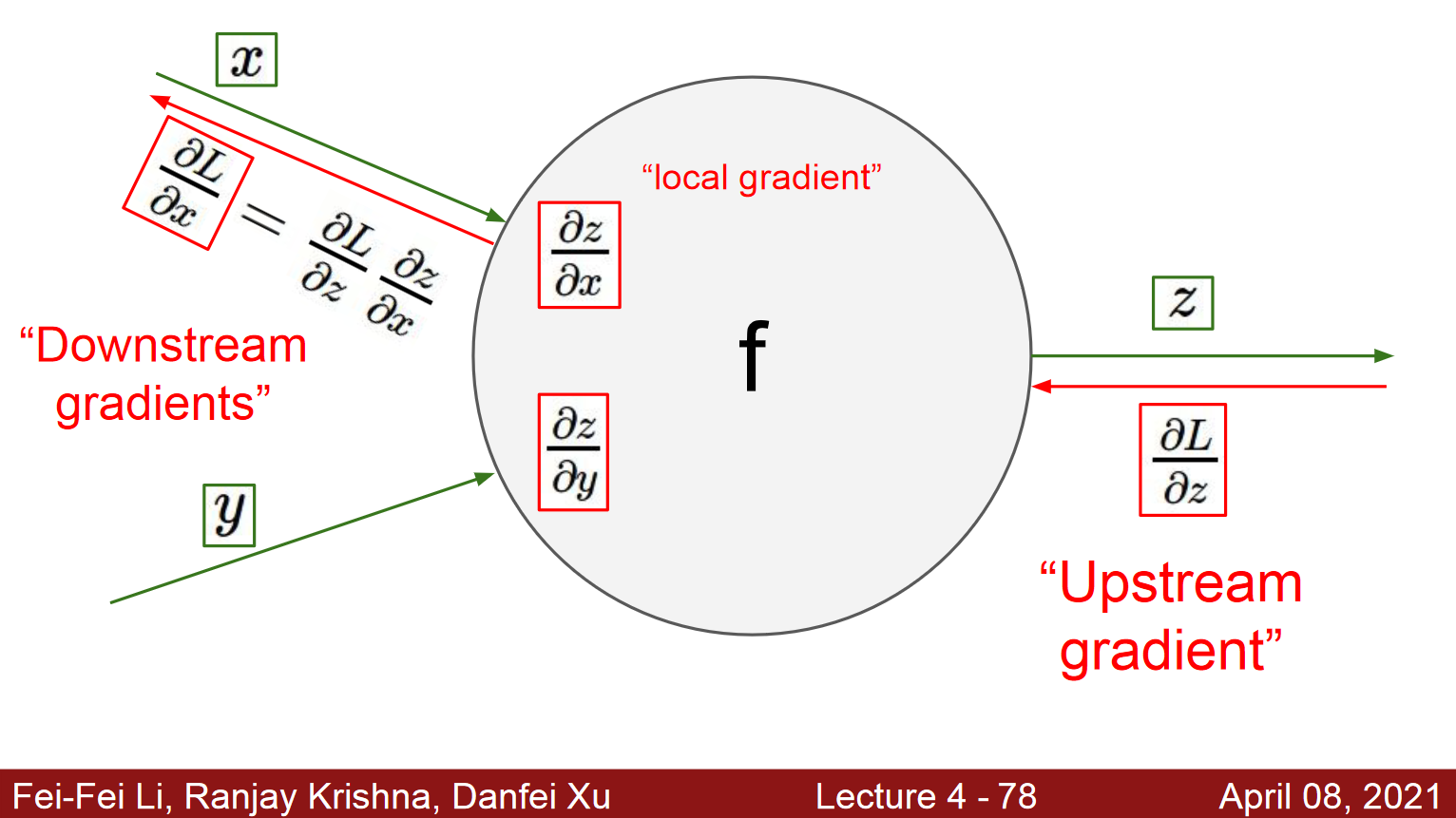
- L은 loss(z-실제값),이것을 내가 원하는 위치(가중치)의 미분을 구한다.
- z에서 구하고 싶으면 L을 z에 대해 미분하고, x에서 구하고 싶으면 (L을 z에 대해 미분한 것) * (z를 x에 대해 미분한 것)(체인룰)
- Downstream gradient는 연산을 통과시키기 이전에 있었던 값이다.
단일 노드역전파
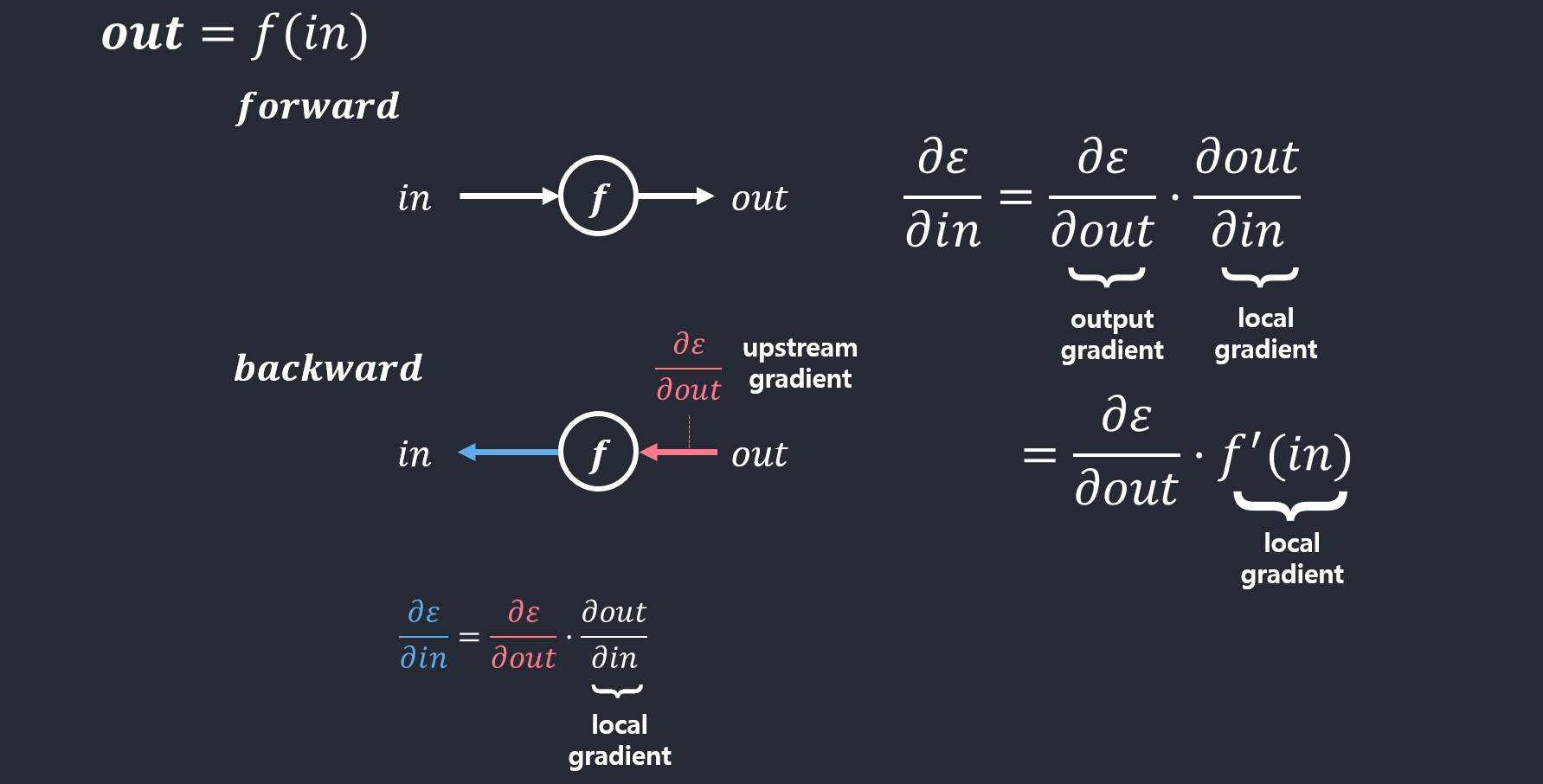
- local gradient: 특정 연산에 의해 나오는 미분값.
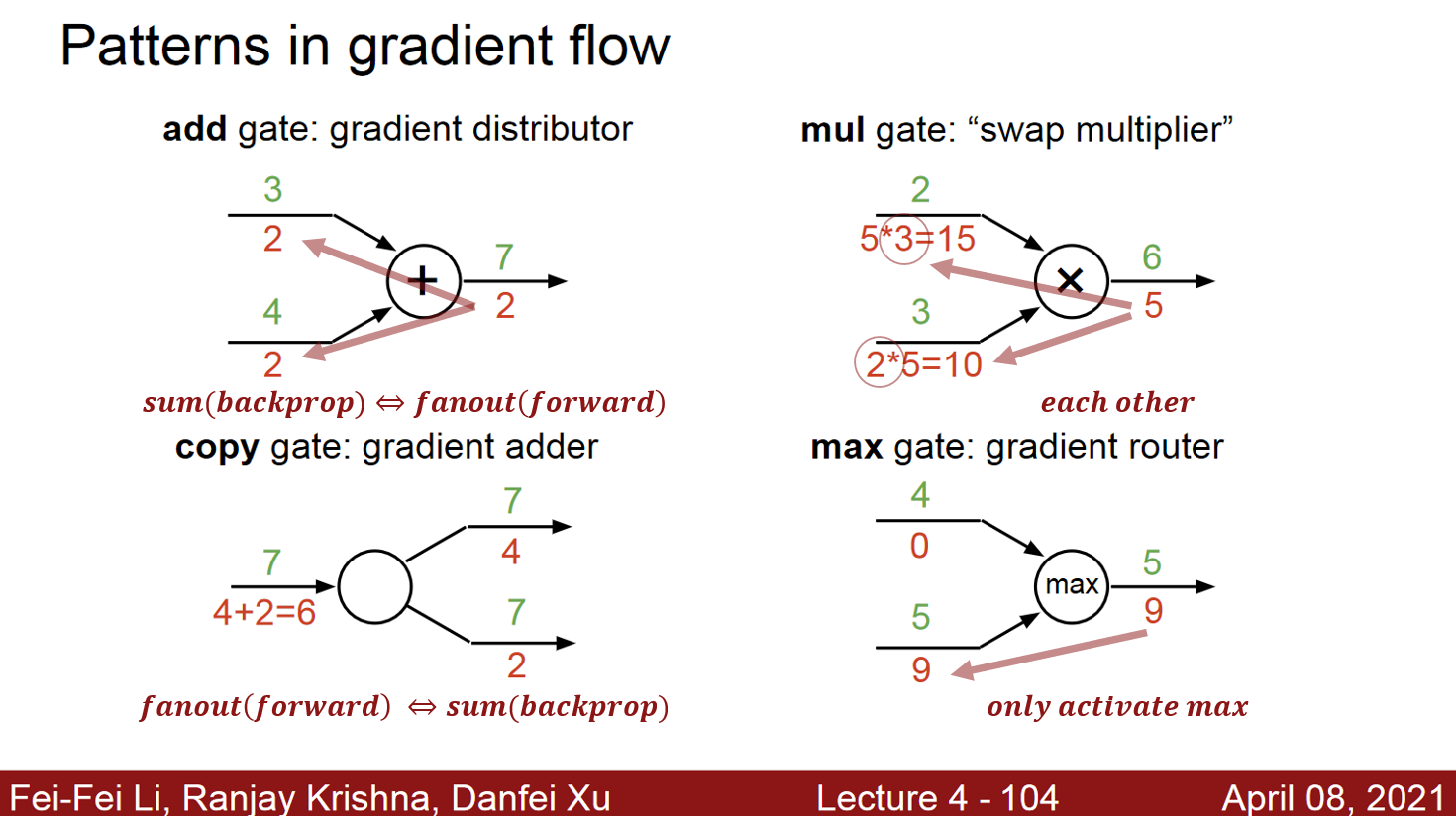
곱셈의 역전파의 예
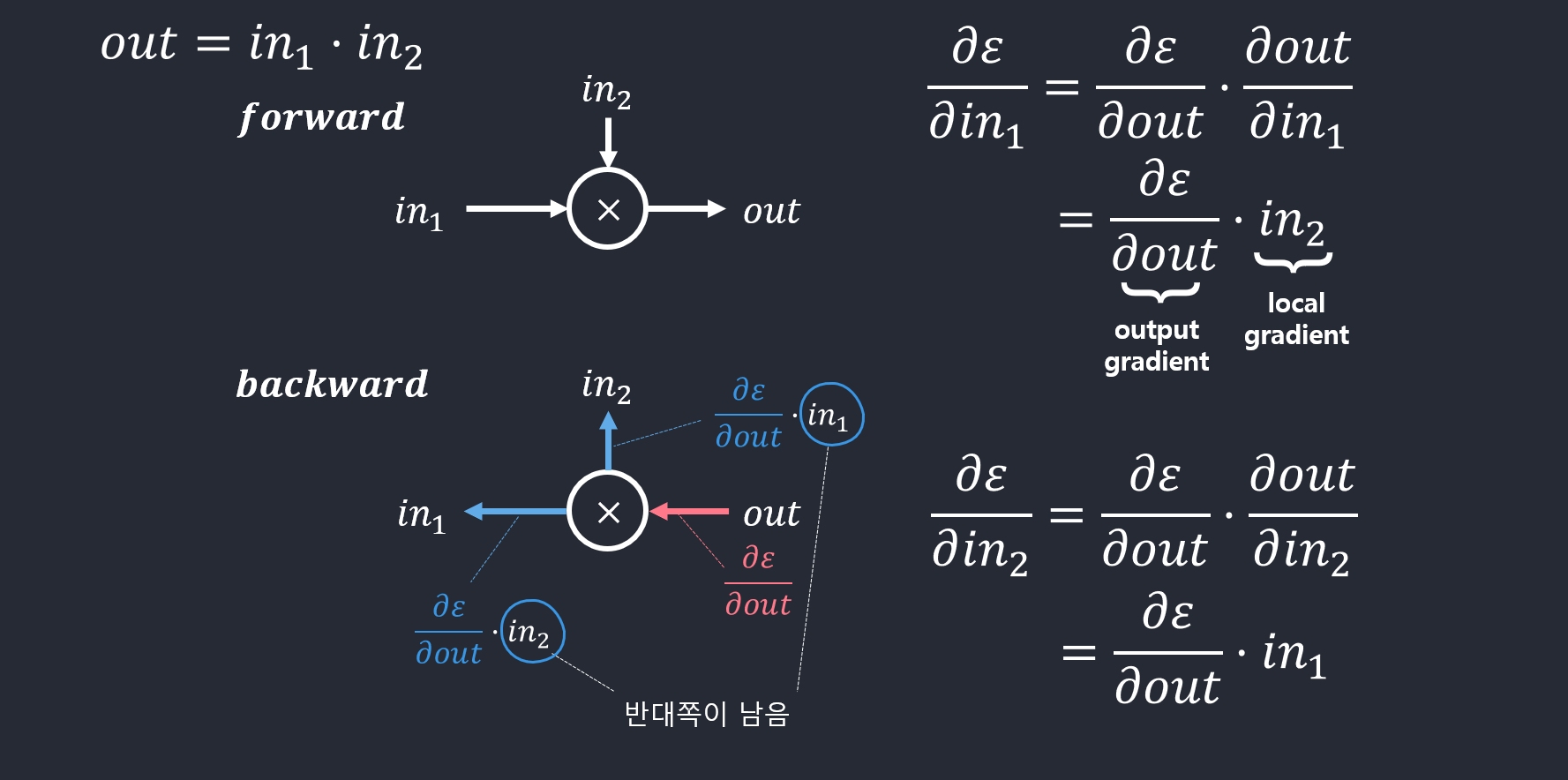
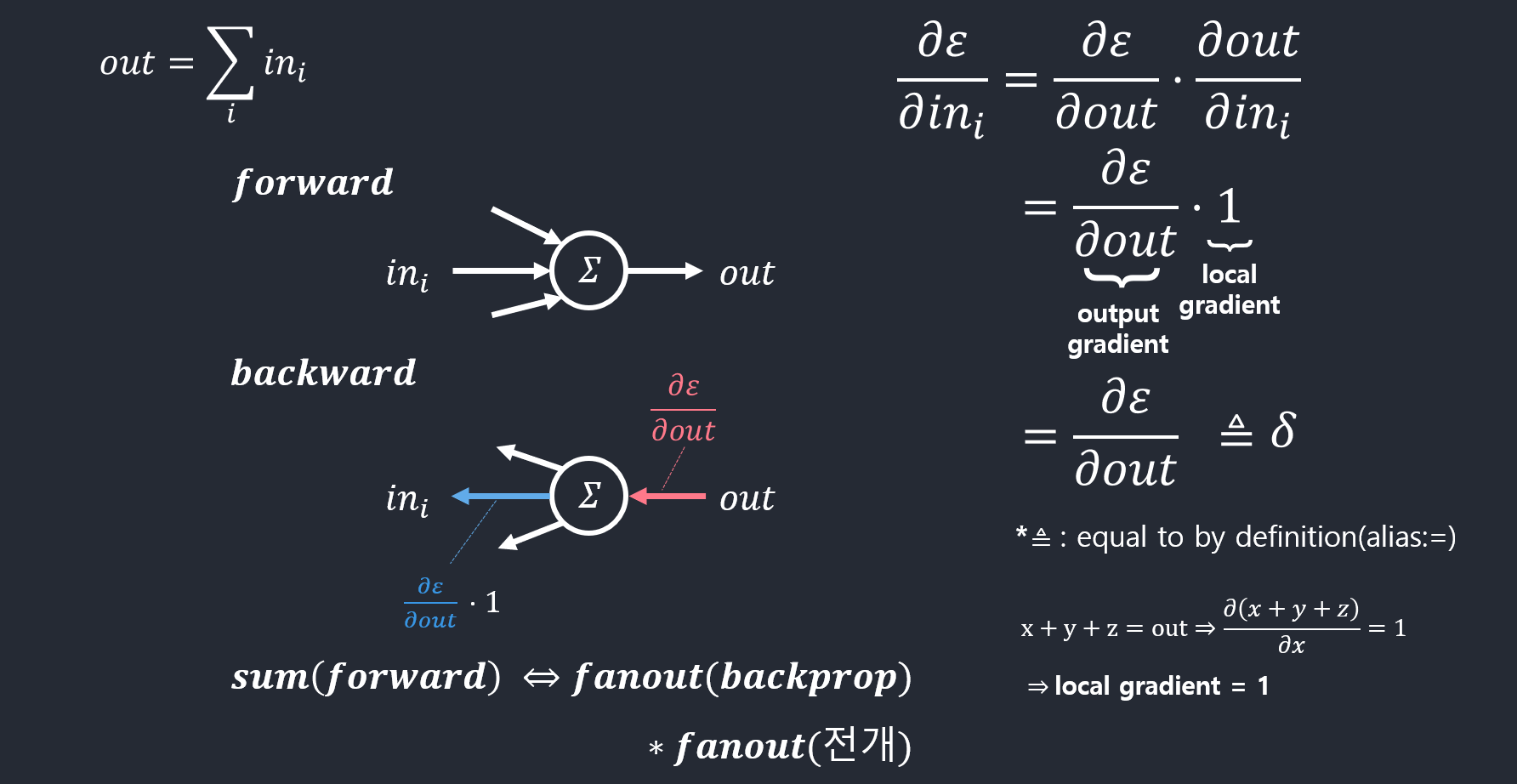
덧셈의 역전파의 예
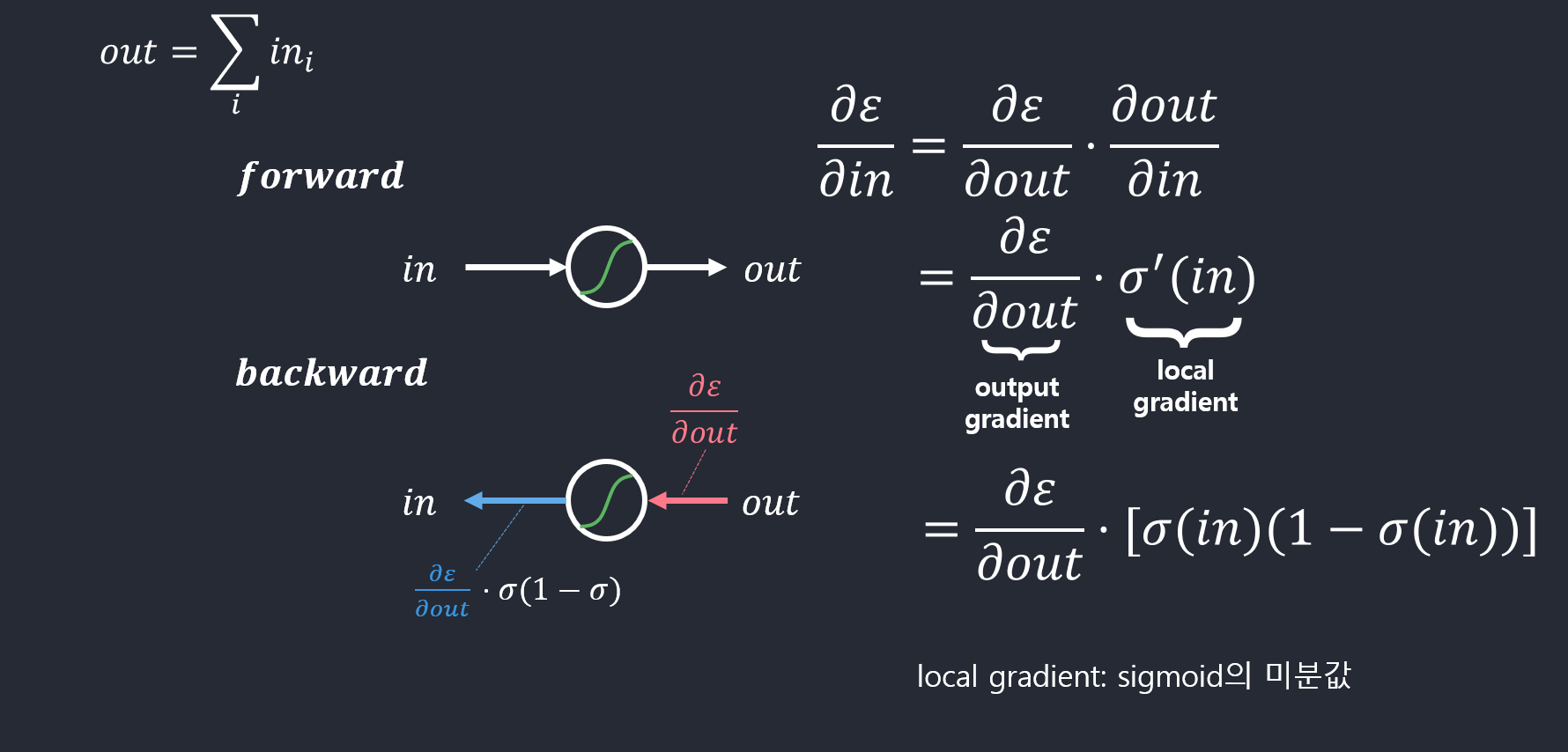
S자 모양 활성함수의 역전파 예
최대화의 역전파 예
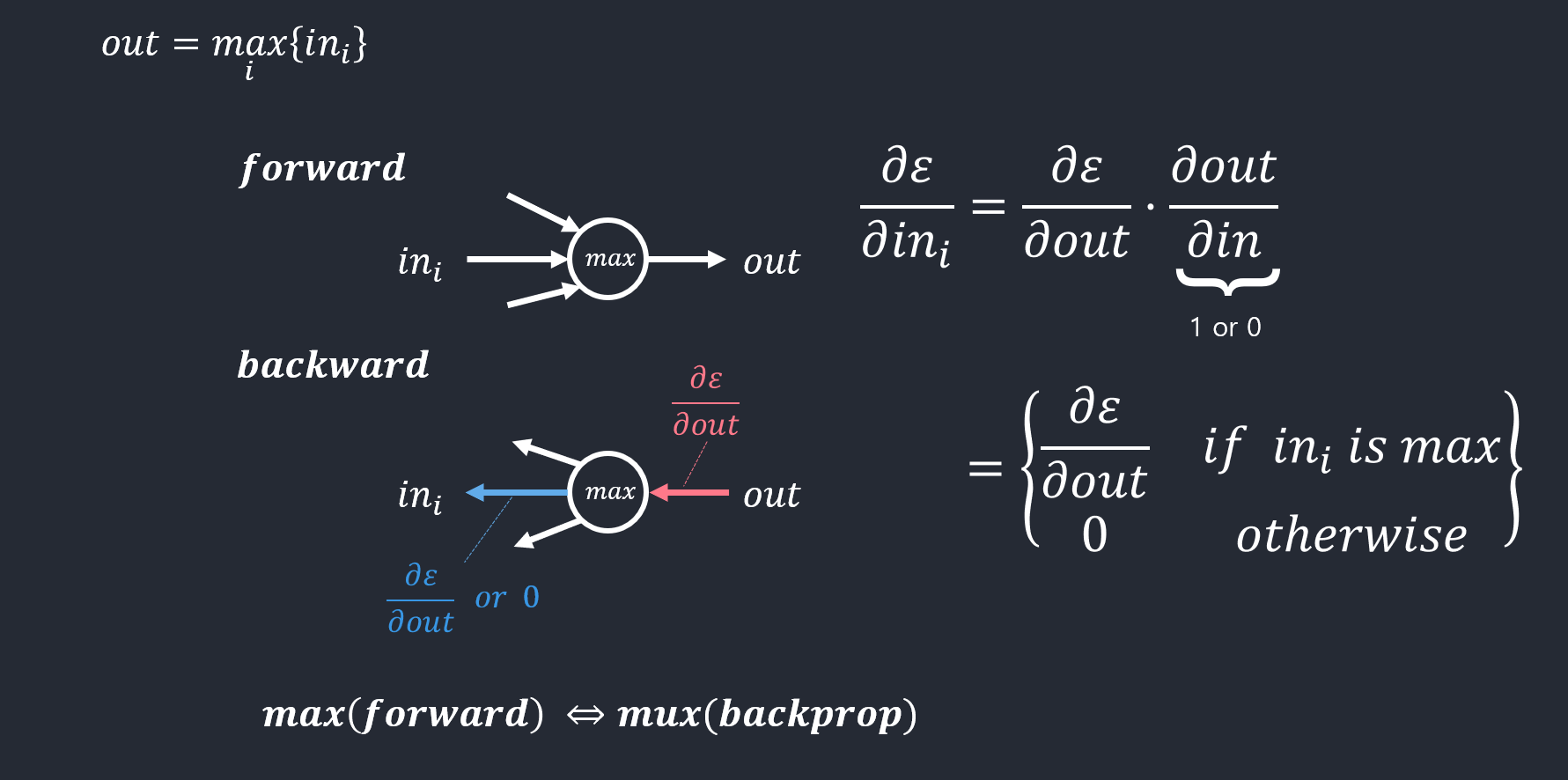
전개의 역전파 예
example 1
practice 1
practice 2
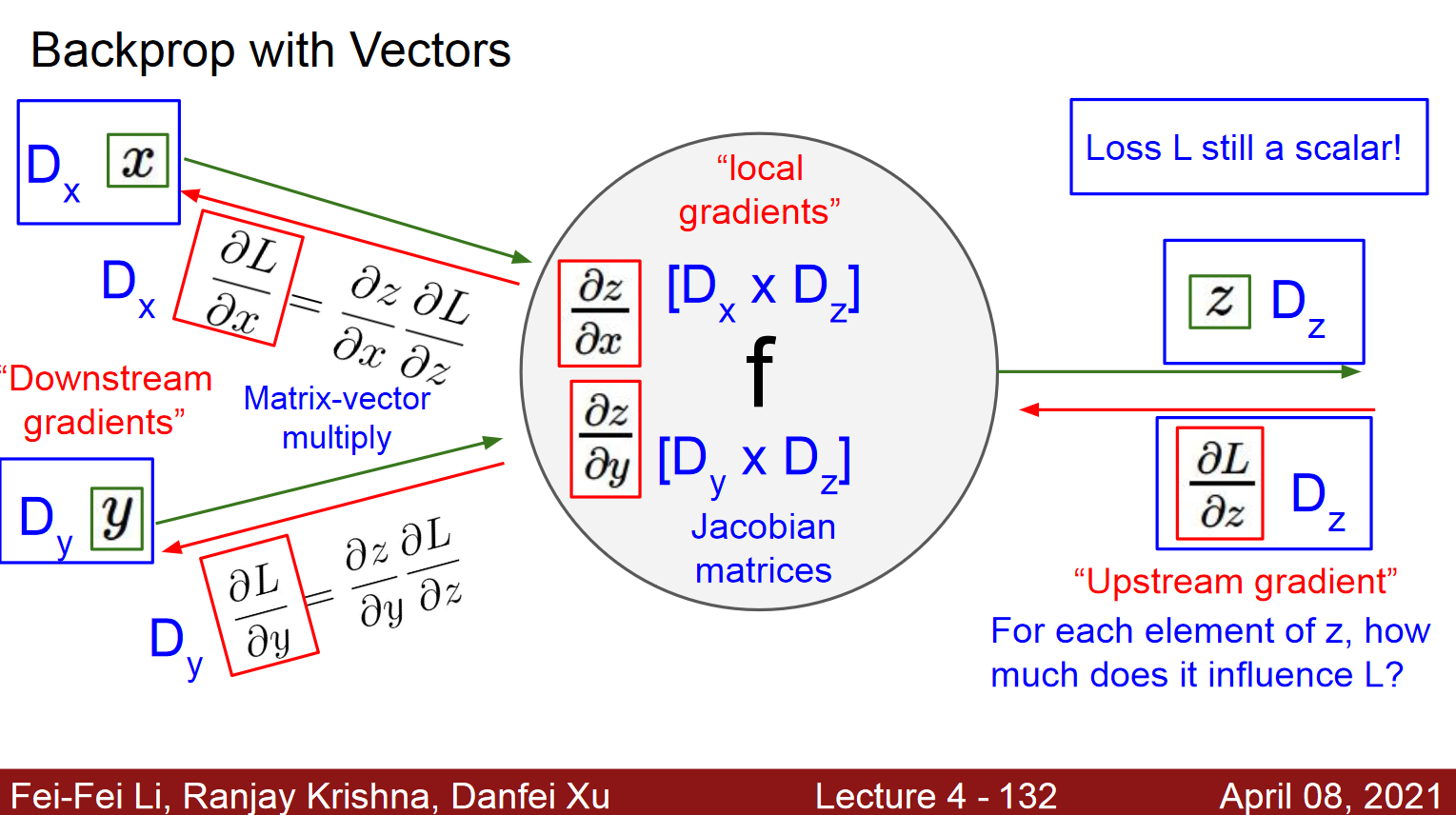
도함수의 종류
- - \(y\)도 벡터, \(x\)도 벡터일때, \(y_1\)과 \(x_1 \sim x_n\)의 모든 조합, \(y_n\)와 \(x_1 \sim x_n\)의 모든 조합, 결국 행렬인데 이것이 Jacobian matrix임
오류 역전파 미분의 연쇄 법칙이용
- 연쇄 법칙
  - 스칼라인 경우, \({dz \above 1pt dx} = {dz \above 1pt dy}{dy \above 1pt dx}\)
  - 벡터인 경우, \(\nabla_{x}z = ({\partial y \above 1pt \partial x})^T \nabla_{y}z\)
    - \(\nabla_{x}z\): z를 x에 대한 gradient
    - x가 m차원 -> y가 n차원 -> 결과가 스칼라 인 경우로 forward인 구조인 경우!
    - \(\frac{\partial z}{\partial x} = \frac{\partial y}{\partial x}\cdot \frac{\partial z}{\partial y}\) 에서 \(\frac{\partial y}{\partial x}\)이 Jacobian Matrix임.
    - \(\frac{\partial z}{\partial y} \Rightarrow \nabla_{y}z\)임
    - 따라서, Jacobian Matrix와 Gradient의 곱으로 표현됨.
      - Jacobian Matrix: \(\frac{\partial y}{\partial x}\)
      - Gradient: \(\nabla_{y}z\)
      - 최종적으로는, \(({\partial y \above 1pt \partial x})^T \nabla_{y}z = \nabla_{x}z\)
    - 예제.
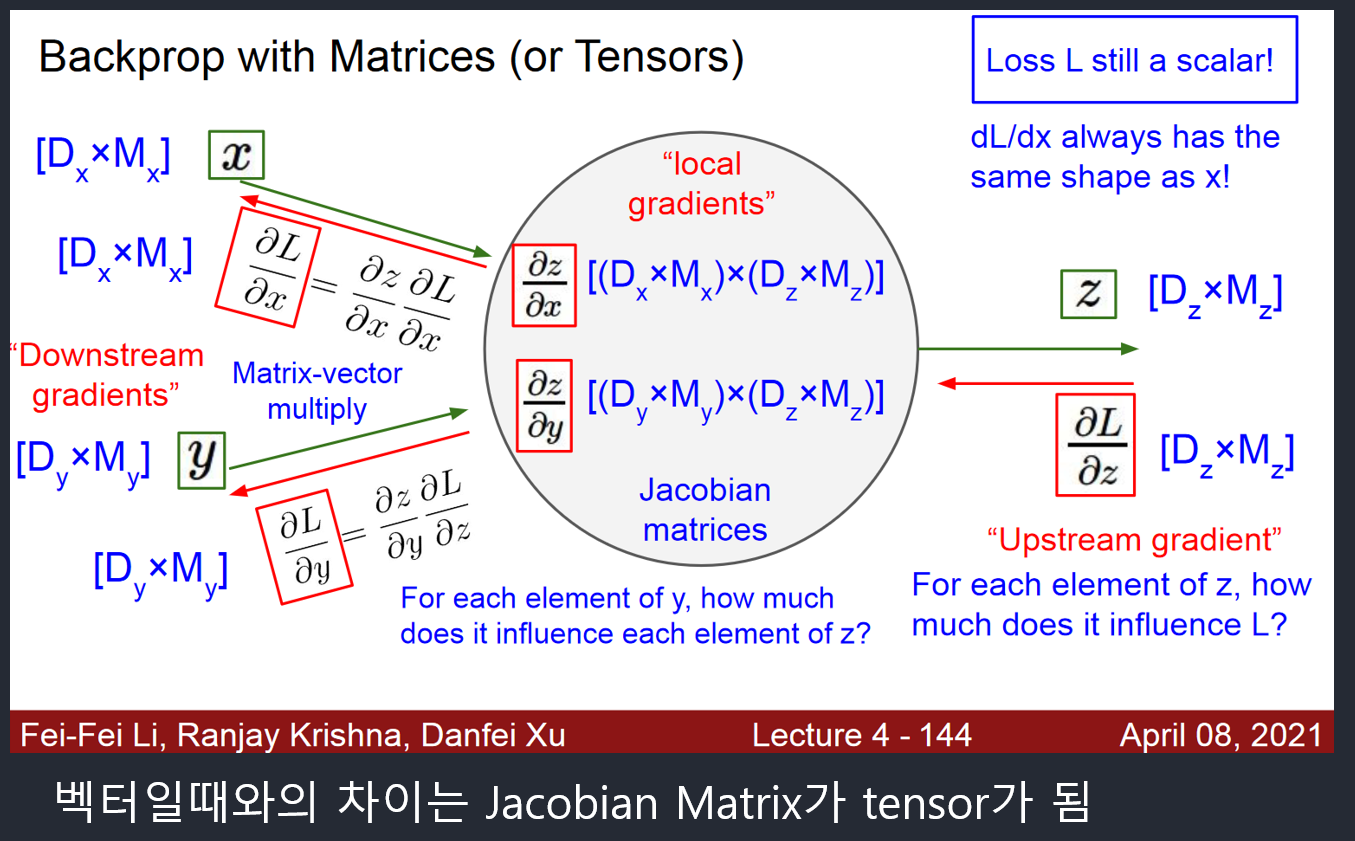
  - Matrix인 경우
행렬 표기 : GPU를 사용한 고속 행렬 연산에 적합.

미니배치 확률론적 경사 하강법

미니배치 방식
- 미니배치(텐서 버전)
- 한번에 t개의 샘플을 처리(t = 미니배치 크기)
  - t=1이면 확률론적 경사 하강법
  - t=n(전체)이면 배치 경사 하강법
- 경사도의 잡음을 줄여주는 효과 때문에 수렴이 빨라짐
- GPU를 사용한 병렬처리에도 유리함
- 현대 기계 학습은 미니배치 기반의 확률론적 경사 하강법을 표준처럼 여겨 널리 사용함.

Appendix

Reference

multilayer-neural-networks: https://slideplayer.com/slide/15275455/
cs231n slides: http://cs231n.stanford.edu/slides/2021/
slides: http://cs231n.stanford.edu/slides/2021/lecture_4.pdf activatoin and gradient: https://adityassrana.github.io/blog/theory/2020/08/26/Weight-Init.html
slide: http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf

Share on

Twitter Facebook LinkedIn

Yilguk Seo 🚀