NN basics - ML & Math

To do

편미분 (partial derivative)

Jacobian Matrix

https://angeloyeo.github.io/2020/07/24/Jacobian.html
https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/jacobian/v/jacobian-prerequisite-knowledge

Hessian Matrix

2차 편도 함수

Linear Algebra

Vector & Matrix

Matrix Multiplication & Vector Tranformation(function or mapping)

\[A\boldsymbol{x} = \boldsymbol{b}\] \[\begin{bmatrix} 4 & -3 & 1 & 3 \\ 2 & 0 & 5 & 1 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 5 \\ 8 \\ \end{bmatrix}\] \[\boldsymbol{x} \in \mathbb{R}^{4} \rightarrow \boldsymbol{b} \in \mathbb{R}^2\]

x라는 vector에 A라는 행렬을 곱했을 때 새로운 공간에 b라는 vector로 투영 됨. (x는 4차원 실수 공간에서 2차원 실수 공간으로)

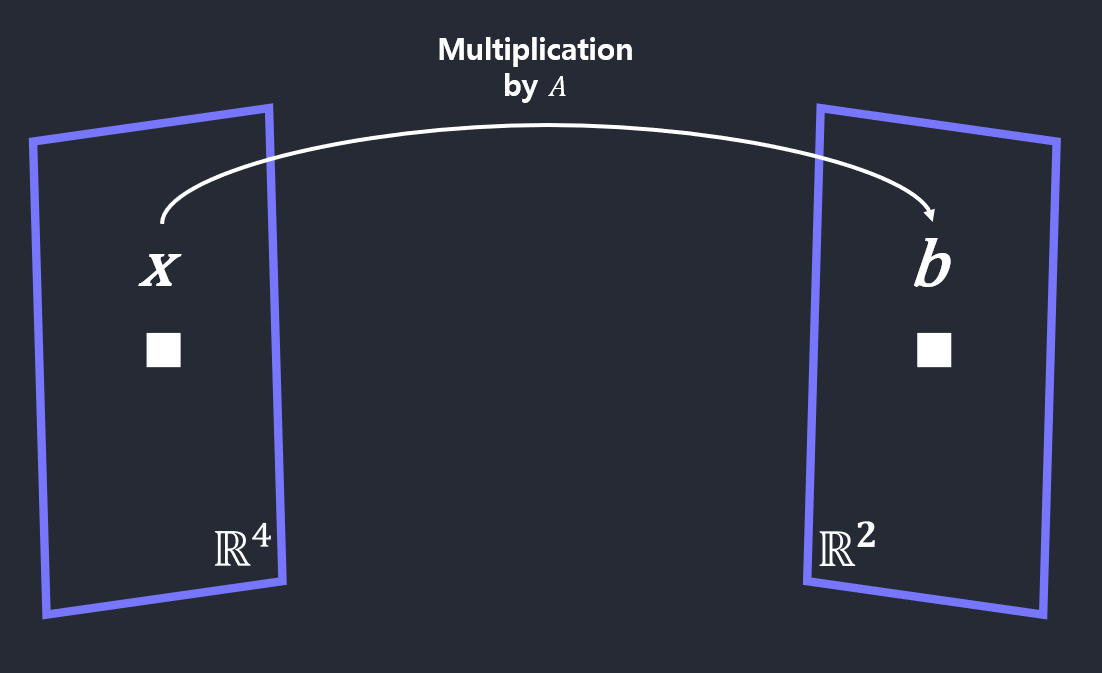
Examples:

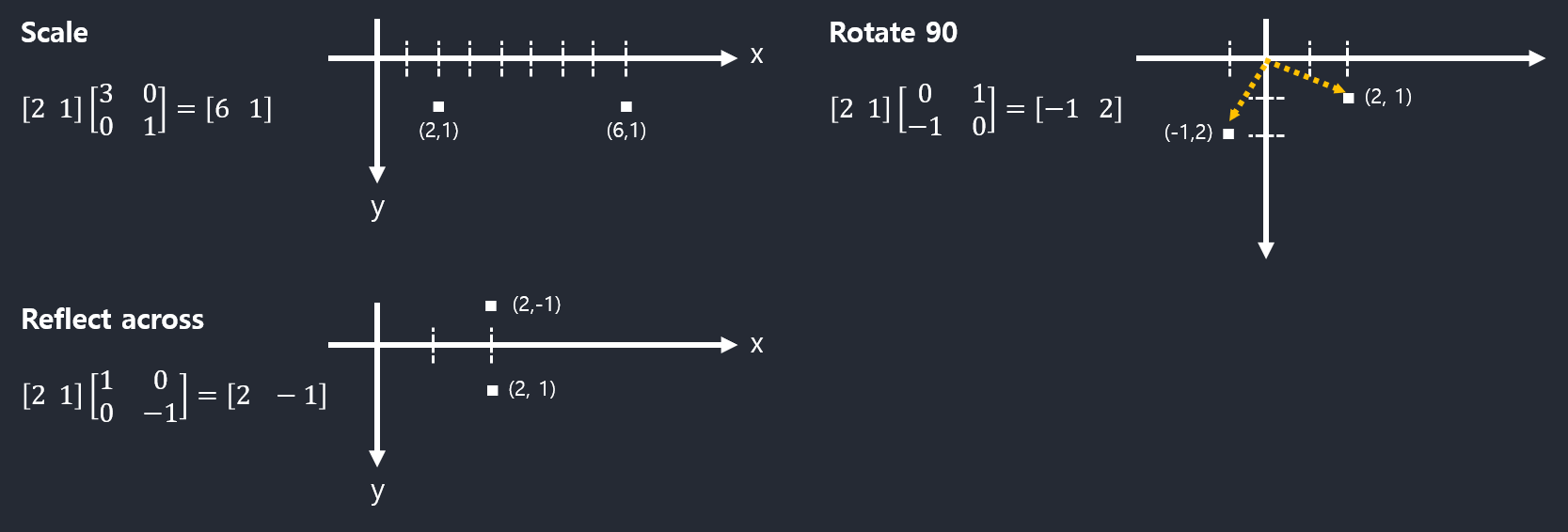
행렬의 곱셉은 그 대상이 벡터든 행렬이든 공간의 선형적 변환.

결국 신경망을 통해 representation learning이 가능한 것.

Representaion Learning

뉴럴네트워크와 Represention Learning

기존대로라면 선형으로 분리할 수 없는 데이터가 선형 분리가 가능하게끔 데이터가 변형됐다는 얘기입니다. 다시 말해 뉴럴네트워크의 학습 과정에서 데이터의 representaion이 (\(x_1,x_2\)) 에서 (\(z_1,z_2\)) 로 바뀐 것.

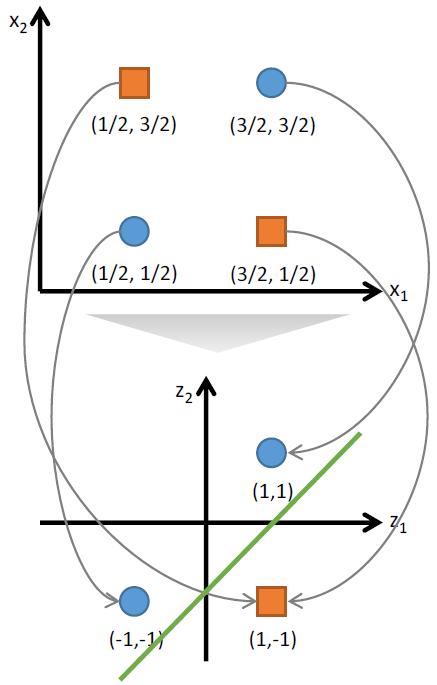
이 글에서는 설명의 편의를 위해 단순 뉴럴네트워크를 예로 들었으나, 깊고 방대한 뉴럴네트워크는 학습데이터가 꽤 복잡한 represention이어도 이를 선형 분리가 가능할 정도로 단순화하는 데 좋은 성능을 낸다고 합니다. 이 때문에 뉴럴네트워크를 representation learner라고 부르는 사람들도 있습니다.

---

representation learning이란, 어떤 task를 수행하기에 적절하게 데이터의 representation을 변형하는 방법을 학습하는 것입니다. 즉 어떤 task를 더 쉽게 수행할 수 있는 표현을 만드는 것입니다. Raw data에 많은 feature engineering과정을 거치지 않고 데이터의 구조를 학습하는 것으로, 딥러닝 아키텍처의 핵심요소라고 할 수 있습니다. 입력 데이터의 최적의 representation을 결정해주고 이 잠재된 representation을 찾는 것을 representation learning 또는 feature learning이라고 부릅니다.

Size of Vector & Matrix (Distance)

유사도는 내적을 통해 어느 정도 구할수 있음.

거리(size)는 Norm 으로 구함.

A norm is a function from a real or complex vector space to the nonnegative real numbers that behaves in certain ways like the distance from the origin.

Vector P Norm

Norm은 벡터의 거리를 측정하는 방법

P Norm

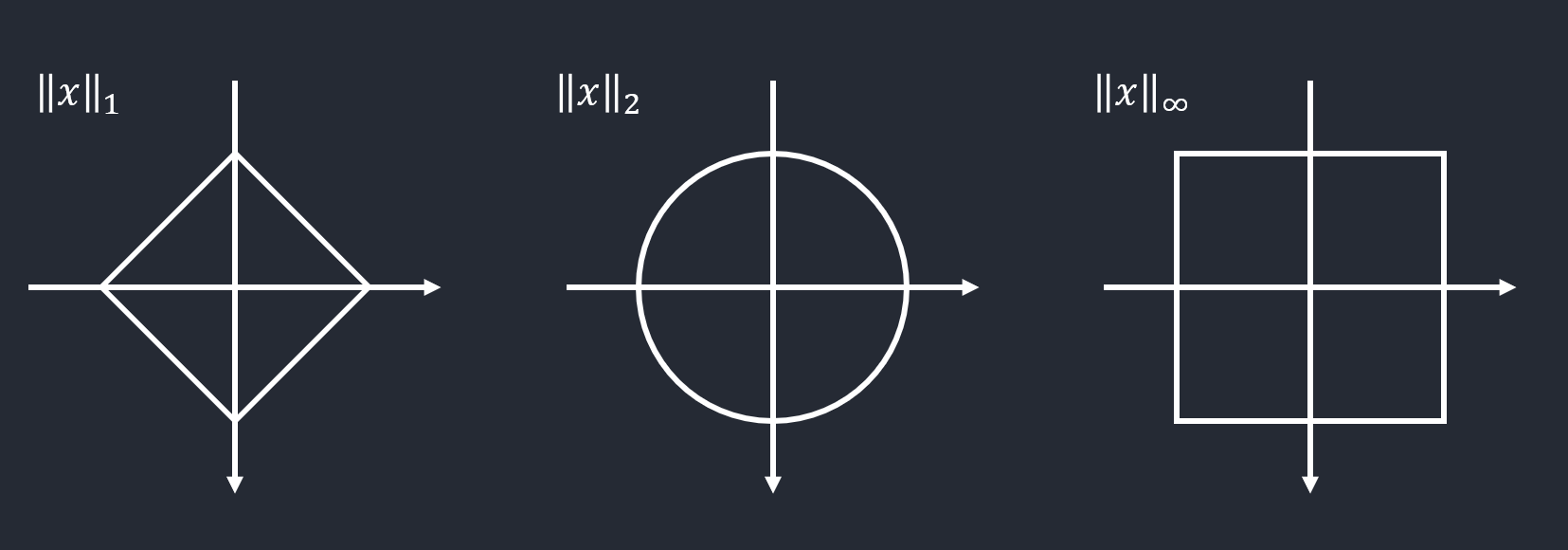
\(\Vert \boldsymbol{x}\Vert = \left(\sum_{i=1,d} \vert x_{i}^{p}\vert \right)^{\frac{1}{p}}\)

Absolute-value Norm(1차 놈)

\(\vert \boldsymbol{x}_{1}\vert_{1}\)

Euclidean Norm(2차 놈)

\(\vert \boldsymbol{x}_{1}\vert_{2}\)

Max Norm

\(\Vert \boldsymbol{x}_{\infty}\Vert = max(\vert x_{1}\vert,\ldots,\vert x_{d}\vert)\)

예, x = (3, -4, 1)일 때, 2차 놈은 \(\Vert \boldsymbol{x}_{1}\Vert_{2} = (3^2 +(-4)^2 + 1^2)^{1/2} \approx 5.099\)
이건 원점으로 부터의 거리를 의미함.

벡터간의 거리도 가능함.
\(\Vert \boldsymbol{z}_{1}\Vert_{2} = ((3-\boldsymbol{a})^2 +(-4-\boldsymbol{b})^2 + (1-\boldsymbol{c})^2)\)

Matrix Frobenious Norm

행렬의 크기를 측정

\[\Vert \boldsymbol{A}\Vert_{F} = \left( \sum_{i=1,n}\sum_{j=1,m}a_{ij}^2 \right)^{\frac{1}{2}}\]

예, \(\boldsymbol{A} = \begin{bmatrix} 2 & 1 \\ 6 & 4 \end{bmatrix}\)일때,

\[\Vert \boldsymbol{A}\Vert_{F} = \sqrt{2^2 + 1^2 + 6^2 + 4^2} = 7.550\]

Norm의 활용

• 거리(크기)의 경우
• Regularization의 경우

  • 

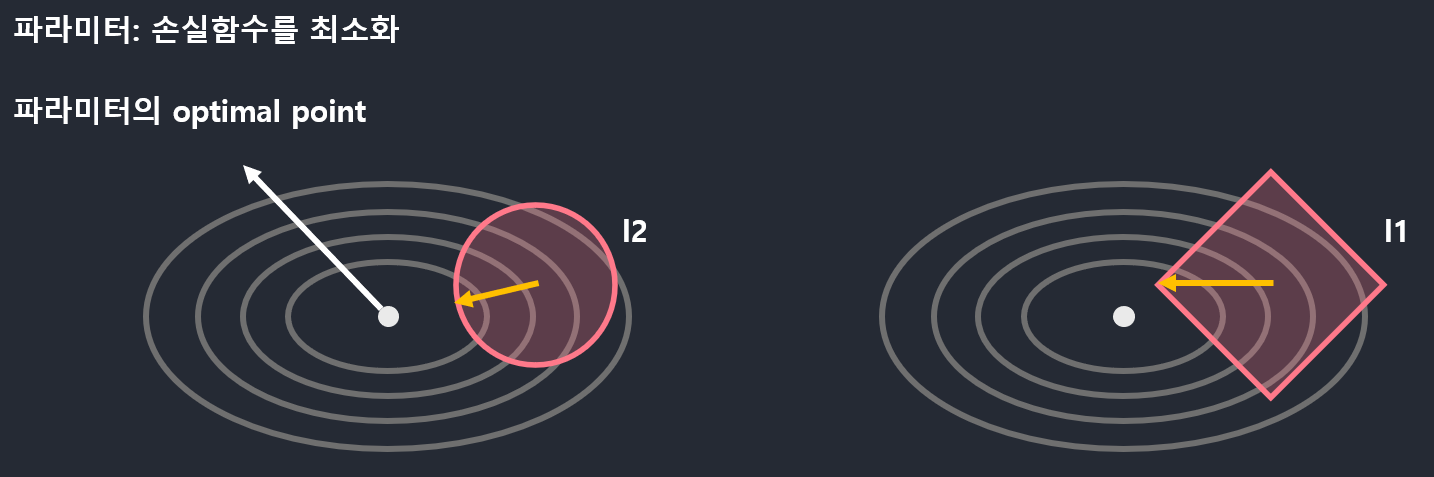
  • optimal point에서 생길수 있는 overfitting을 해결하기 위해 optimal point에 도달하지 못하도록 l2 norm의 boundary안에서 optimal point와의 최소값을 가지도록 Gradient에 Norm을 추가하는 형태로 사용함.

퍼셉트론 (Perceptron)

input \(\boldsymbol{x}\)와 \(\boldsymbol{W}\)를 내적한 것이 결과값인데 이 결과값에 activation function을 적용해서 threshold 기준으로 + or - 형태로 도출하는 것이다.

내적이 중요한 이유는 내적을 통해 나온 scalar값이 activation function의 input으로 들어가기 때문이다.

공간적으로 보면,
학습을 통해 얻어진 \(\boldsymbol{W}\)와 input 이 내적을 한 값을 \(\boldsymbol{W}\)에 대해 \(\text{Proj}\)했을 때의 위치가, decision boundary 상에서 어디에 위치해 있느냐.
이 \(\text{Proj}\) 값이 퍼셉트론의 activation function이 정한 threshold(T) 보다 크거나 같을 경우 1, 아니면 -1을 ouput으로 나와서 분할 해주는 것임.

\(\boldsymbol{W}\)에 수직인 Decision boundary는 2차원일때는 decision line, 3차원일때는 decision plane, 4차원 이상은 decision hyperplane.

결정 경계 (decision boundary)는 선형판별함수 \(y(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+w_0\)가 0을 만족시키는 \(\boldsymbol{x}\)의 집합
만약 bias를 사용할 경우 bias(\(w_0\))가 결정 경계를 결정하는 요소가 됨(기울기는 같지만 위치 다른).
여기를 참조.

Linear Classifier (cs231n)

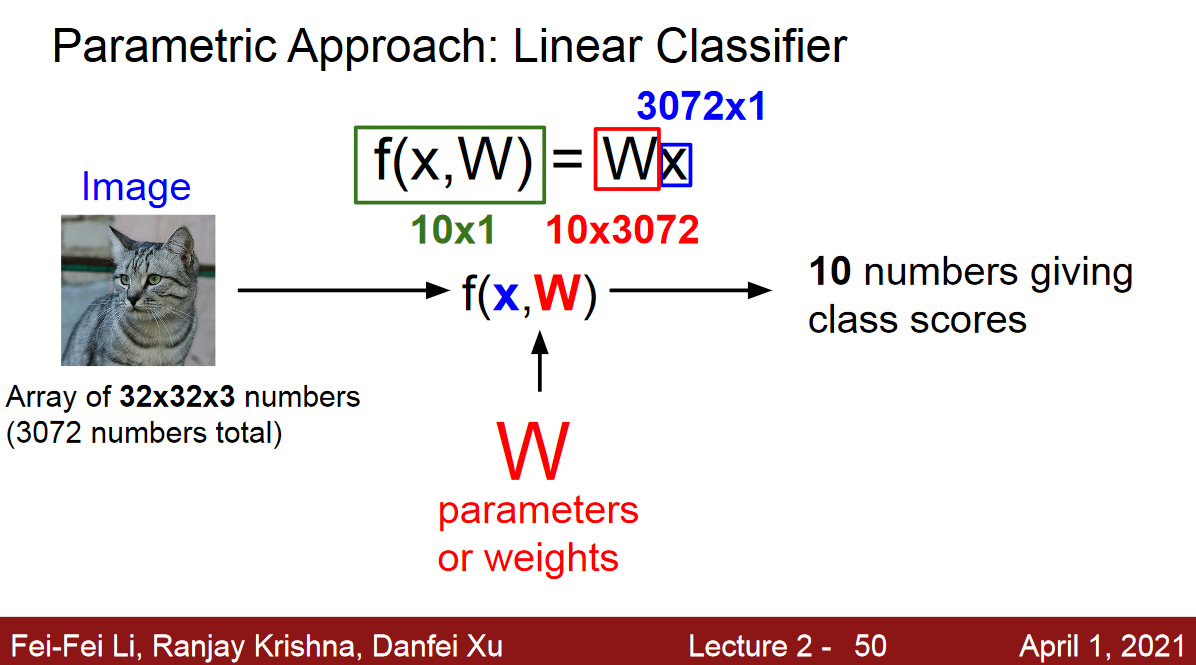
이미지 X(tensor)를 flatten 시켜서 32 x 32 x 3인 데이터를 3072 x 1의 shape인 vector으로 만들어서 입력값으로 넣어줄 것이고,
W는 10 x 3072의 shape으로 만들어서 이 행렬과 input vector와의 내적으로 나온 값이 10 x 1의 shape을 취하게 만들어줌. (10개의 퍼셉트론이 있다고 보면 됨)
10개의 target shape을 만든 것은 임의임. 3개의 target class를 원한다면 3 x 1의 shape으로 적용하면 됨.

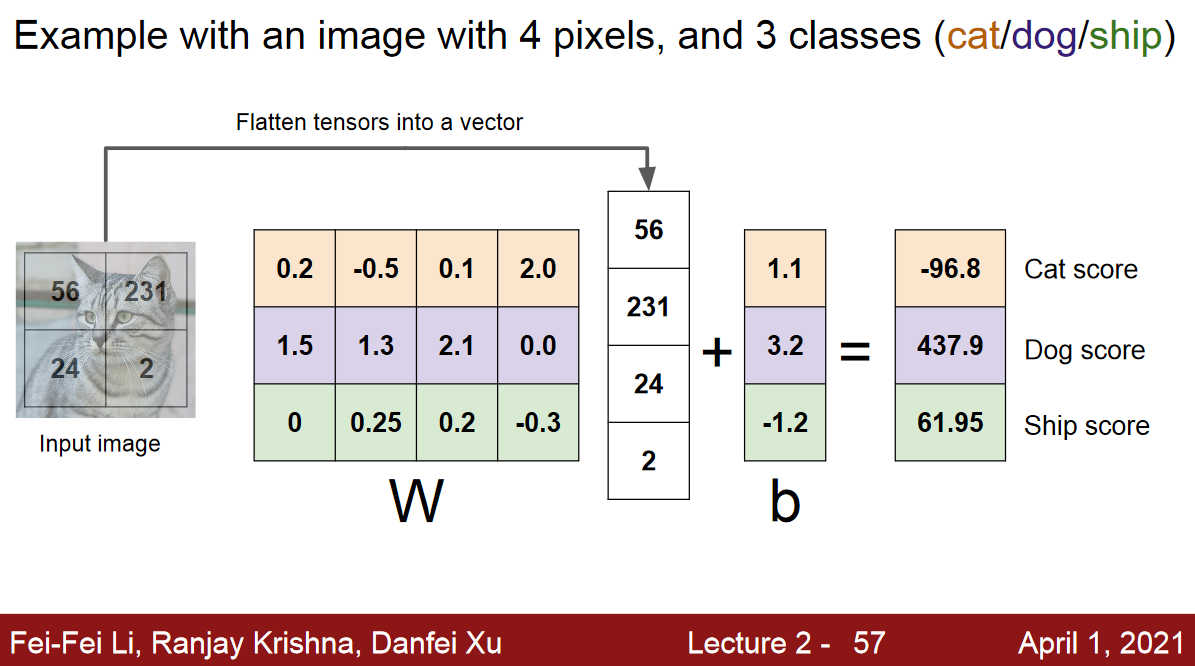
아래의 slide를 보면,
cat, dog and ship인 3개의 클래스로 구분하는 예제를 보여주기 위해서 W의 shape이 3 x 4임을 알 수 있음.

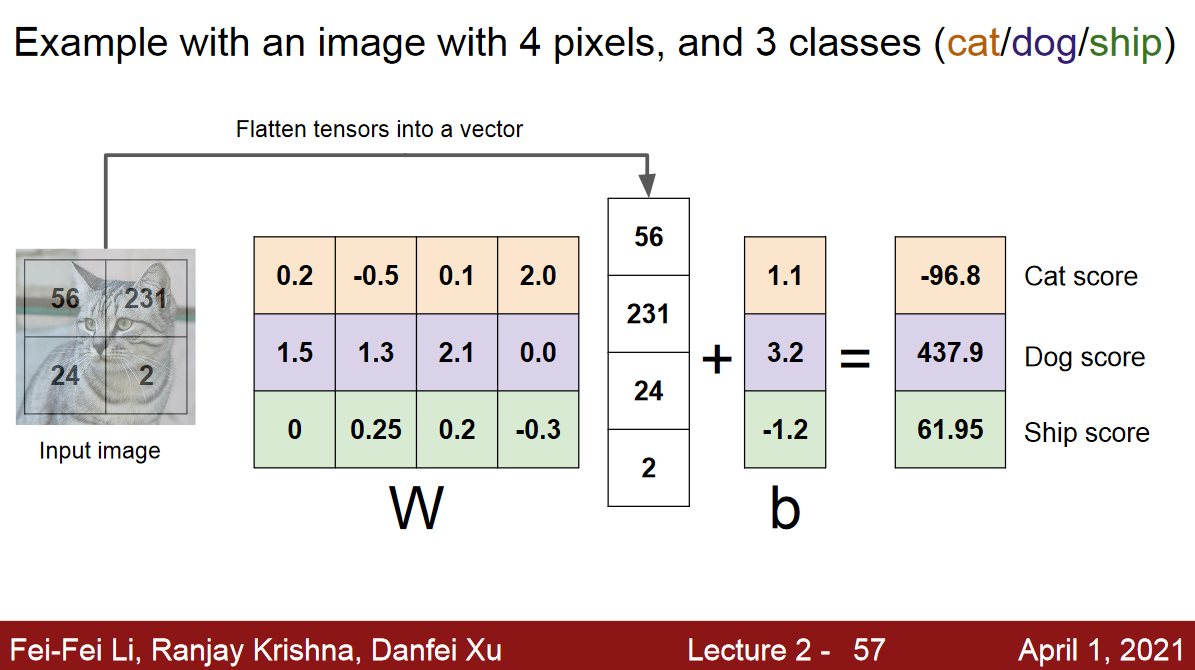
퍼셉트론 하나가 선형 분류기 1개라고 생각하면 됨.

cs231n:
The problem is that the linear classifier is only learning one template for each class.
So, if there’s sort of variations in how that class might appear, it’s trying to average out all those different variations, all those different appearances, and use just one single template to recognize each of those categories.

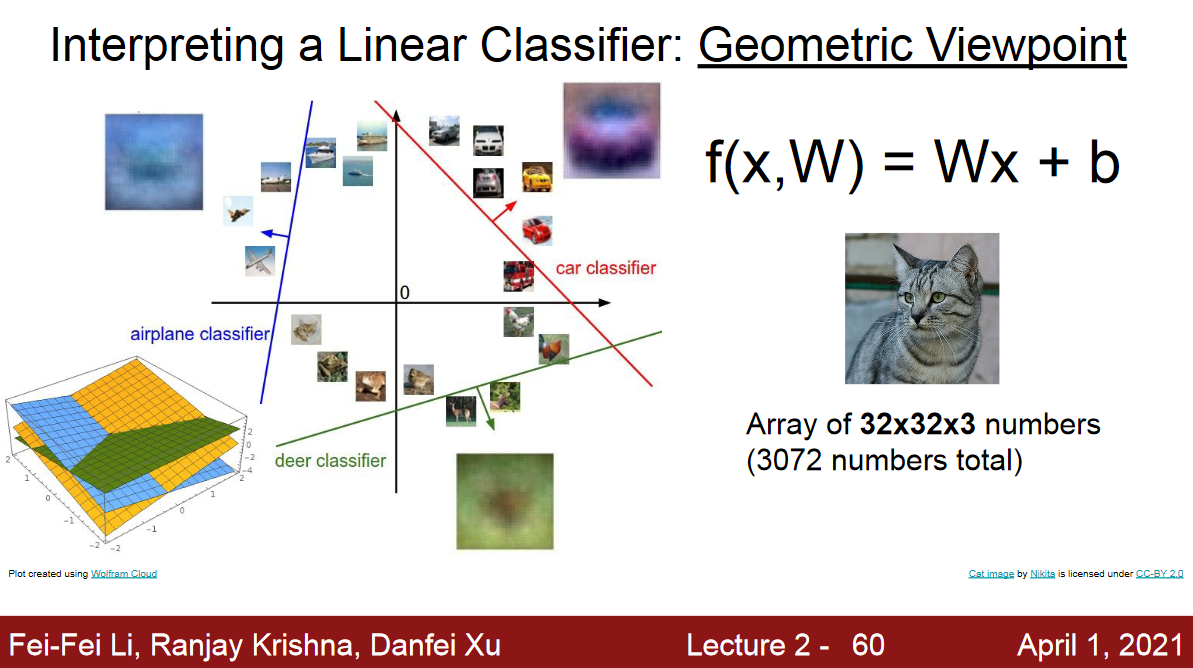
Images as points in high dimensional space. The linear classifier is putting in these linear decision boundaries to try to draw linear separation between one category and the rest of the categories.

역행렬 (Inverse Matrix)

vector를 transform 시킨 다음 다시 원공간으로 되돌리기 위해 사용됨.

공간의 변화를 사용하는 기계학습 모델이나 가설(PCA 같은 경우)을 사용하는 경우에 역행렬이 가능하면 편리해지는 부분이 존재함.

선형대수에서 역행렬을 통해 방정식을 보다 편리하게 풀기 위함.

• 가역행렬(Invertible Matrix)의 조건 중 중요한 것.
  • \(\boldsymbol{A}\)의 모든 행과 열이 선형독립이다.
  • \(\det(\boldsymbol{A}) \neq 0\).
  • \(\boldsymbol{A}^{T}\boldsymbol{A}\)는 positive definite 대칭행렬임.
  • \(\boldsymbol{A}\)의 eigenvalue는 모두 0이 아니다.

행렬식 (Determinant)

기하학적 의미: 행렬의 곱에 의한 공간의 확장 또는 축소 해석

• \(\det(\boldsymbol{A}) = 0\): 하나의 차원을 따라 축소되어 부피를 잃게 됨
• \(\det(\boldsymbol{A}) = 1\): 부피 유지한 변환/방향 보존 됨
• \(\det(\boldsymbol{A}) = -1\): 부피 유지한 변환/방향 보존 안됨
• \(\det(\boldsymbol{A}) = 5\): 5배 부피 확장되며 방향 보존

원공간에 대한 변환의 부피의 변화를 측정하는 것임.

정부호 행렬 (positive definite matrices)

행렬의 공간의 모습을 판단하기 위해?
양의 정부호 행렬: 0이 아닌 모든 벡터 \(\boldsymbol{x}\)에 대해, \(\boldsymbol{x}^{T}\boldsymbol{A}\boldsymbol{x} > 0\)
성질

• 고유값 모두 양수
• 역행렬도 정부호 행렬
• \(\det(\boldsymbol{A}) = 0\).

분해 (Decomposition)

고유값 분해 (Eigen-decomposition)

ML-Basics-Linear-Algebra 참조.

정방행렬 \(A\in \mathbb{R}^{n\times n}\) 이 주어졌을 때, \(Ax = \lambda x, x\neq 0\)을 만족하는 \(\lambda \in \mathbb{C}\)를 \(A\)의 고유값(eigenvalue) 그리고 \(x\in \mathbb{C}^n\)을 연관된 고유벡터(eigenvector)라고 부른다.

Eigenvectors: 선형변환(T)이 일어난 후에도 방향이 변하지 않는 영벡터가 아닌 벡터.

Eigenvalues: Eigenvectors의 길이가 변하는 배수(scale), reversed나 scaled가 될 수 있지만 방향은 변하지 않는다.
They make for interesting basis vectors. Basis vectors whos transformation matrices are maybe computationally more simpler or ones that make for better coordinate systems.

numpy.linalg 모듈의 eig 함수를 사용하여 고유값과 고유벡터를 구할 수 있다.

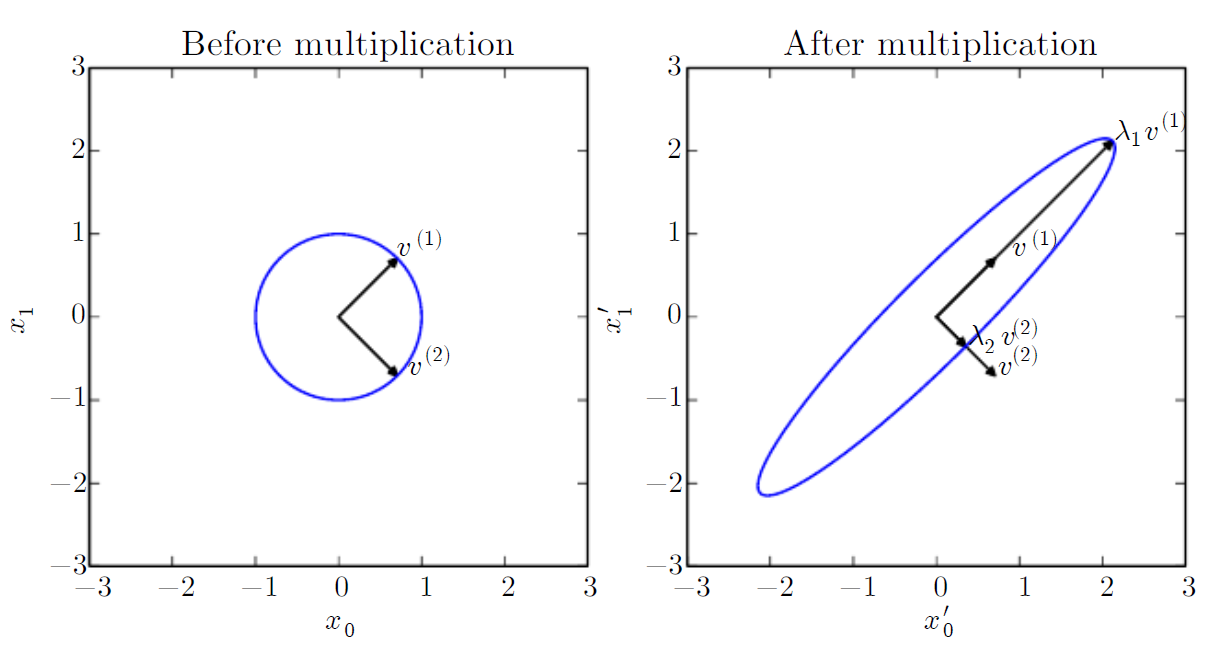
Figure 2.3: An example of the effect of eigenvectors and eigenvalues. Here, we have a matrix A with two orthonormal eigenvectors, v(1) with eigenvalue λ1 and v(2) with eigenvalue λ2. (Left) We plot the set of all unit vectors u ∈ R2 as a unit circle. (Right) We plot the set of all points Au. By observing the way that A distorts the unit circle, we can see that it scales space in direction v(i) by λi. Deep Learning. Ian Goodfellow, Yoshua Bengio, and Aaron Courville.

고유값 분해를 통해서 행렬의 역행렬도 구할 수 있고, PCA에서도 활용함.

고유값 분해는 정사각 행렬에만 적용됨.
하지만, ML에서 항상 정사각 행렬만 존재한다는 보장이 없기 때문에 SVD를 사용.

특잇값 분해 (SVD: Singular Value Decomposition)

정사각 행렬이 아닌 행렬의 역행렬을 계산하기 위해 사용됨

특이값분해(SVD)의 기하학적 의미

행렬을 \(x' = Ax\)와 같이 좌표공간에서의 선형변환으로 봤을 때 직교행렬(orthogonal matrix)의 기하학적 의미는 회전변환(rotation transformation) 또는 반전된(reflected) 회전변환, 대각행렬(diagonal maxtrix)의 기하학적 의미는 각 좌표성분으로의 스케일변환(scale transformation)이다.

행렬 \(R\)이 직교행렬(orthogonal matrix)이라면 \(RR^T = E\)이다. 따라서 \(\det(RR^T) = \det(R)\det(R^T) = \det(R^2) = 1\)이므로 \(\det(R)\)는 항상 +1, 또는 -1이다. 만일 \(\det(R)=1\)라면 이 직교행렬은 회전변환을 나타내고 \(\det(R)=-1\)라면 뒤집혀진(reflected) 회전변환을 나타낸다.

👉 따라서 식 \((1), A = U\Sigma V^T\)에서 \(U, V\)는 직교행렬, \(\Sigma\)는 대각행렬이므로 \(Ax\)는 \(x\)를 먼저 \(V^T\)에 의해 회전시킨 후 \(\Sigma\)로 스케일을 변화시키고 다시 \(U\)로 회전시키는 것임을 알 수 있다.

<그림1> 출처: 위키피디아

👉 즉, 행렬의 특이값(singular value)이란 이 행렬로 표현되는 선형변환의 스케일 변환을 나타내는 값으로 해석할 수 있다.

👉 고유값분해(eigendecomposition)에서 나오는 고유값(eigenvalue)과 비교해 보면 고유값은 변환에 의해 불변인 방향벡터(-> 고유벡터)에 대한 스케일 factor이고, 특이값은 변환 자체의 스케일 factor로 볼 수 있다.

👉 이 주제와 관련하여 조금 더 상상의 나래를 펴 보면, \(m \times n\) 행렬 \(A\)는 \(n\)차원 공간에서 \(m\)차원 공간으로의 선형변환이다. \(n\)차원 공간에 있는 원, 구 등과 같이 원형으로 된 도형을 \(A\)에 의해 변환시키면 먼저 \(V^T\)에 의해서는 회전만 일어나므로 도형의 형태는 변하지 않는다. 그런데 \(\Sigma\)에 의해서는 특이값의 크기에 따라서 원이 타원이 되거나 구가 럭비공이 되는 것과 같은 식의 형태변환이 일어난다 (\(n\)이 2차원인 원의 경우 첫번째 특이값 \(\sigma_1\)은 변환된 타원의 주축의 길이, 두번째 특이값 \(\sigma_2\)는 단축의 길이에 대응된다). 이후 \(U\)에 의한 변환도 회전변환이므로 도형의 형태에는 영향을 미치지 못한다. 만일 \(m > n\)이라면 0을 덧붙여서 차원을 확장한 후에 \(U\)로 회전을 시키는 것이고 \(m < n\)이라면 일부 차원을 없애버리고(일종의 투영) 회전을 시키는 셈이다. 결국 선형변환 \(A\)에 의한 도형의 변환결과는 형태적으로 보면 오로지 A의 특이값(singular value)들에 의해서만 결정된다는 것을 알 수 있다.

Information Theory & Optimization (chapter 3 in Deep Learning book)

확률 분포간의 유사성을 정량화

정보이론의 기본원리 👉 확률이 작을수록 많은 정보
unlikely event의 정보량이 많음.

자기 정보 (self information)

사건(메시지, \(e_i\))의 정보량 (로그 밑이 2인 경우 bit, 자연상수인 경우 nat)
\(h(e_i) = -log_{2}P(e_{i})\) or \(h(e_i) = -log_{e}P(e_{i})\)

예, 동전 앞면이 나오는 사건의 정보량:
\(log_{2}(\frac{1}{2}) = 1\)
1~6인 주사위에서 1이 나오는 사건의 정보량:
\(-log_{2}(\frac{1}{6}) \approx 2.58\)

후자의 사건이 상대적으로 높은 정보량을 갖는다고 말할 수 있음.

엔트로피 (Entropy)

확률 변수 \(x\)의 불확실성을 나타내는 엔트로피
모든 사건 정보량의 기댓값으로 표현

이산확률분포 \(H(x) = - \sum_{i=1, k}P(e_i)log_{2}P(e_i)\) 또는 \(H(x) = - \sum_{i=1, k}P(e_i)log_{e}P(e_i)\)
연속확률분포 \(H(x) = - \int_{\mathbb{R}}P(x)log_{2}P(x)\) 또는 \(H(x) = - \int_{\mathbb{R}}P(x)log_{e}P(x)\)

예, 동전의 앞뒤의 발생 확률이 동일한 경우의 엔트로피는 다음과 같음

\[\begin{align}H(x) &= - \sum_{i=1, k}P(e_i)logP(e_i) \\ &= - (0.5\times log_{2}0.5 + 0.5\times log_{2}0.5) \\ &= -log_{2}0.5 \\ &= -(-1) \end{align}\]

동전의 발생 확률에 따른 엔트로피 변화 (binary entrophy)

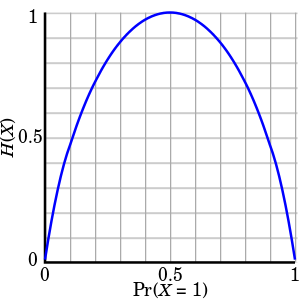
• 공평한 동전일 경우 가장 큰 엔트로피를 구할 수 있음
• 동전 던지기 결과 전송에는 최대 1비트가 필요함을 의미

모든 사건이 동일한 확률을 가질 때, 즉, 불확실성이 가장 높은 경우, 엔트로피가 최대 값을 갖는다.

예, 윷과 pair 주사위(1~6)의 엔트로피 값을 비교.

윷: \(H(x) = - (\frac{4}{16}log_{2}\frac{4}{16} + \frac{6}{16}log_{2}\frac{6}{16} + \frac{4}{16}log_{2}\frac{4}{16} + \frac{1}{16}log_{2}\frac{1}{16} + \frac{1}{16}log_{2}\frac{1}{16}) \approx 2.0306 \text{비트}\)

주사위: \(H(x) = - (\frac{1}{6}log_{2}\frac{1}{6} + \frac{1}{6}log_{2}\frac{1}{6} + \frac{1}{6}log_{2}\frac{1}{6} + \frac{1}{6}log_{2}\frac{1}{6} + \frac{1}{6}log_{2}\frac{1}{6} + \frac{1}{6}log_{2}\frac{1}{6}) \approx 2.585 \text{비트}\)

교차 엔트로피 (Cross Entropy)

두 개의 확률 분포가 얼마 만큼의 정보를 공유하는 가.

\[H(P,Q) = - \sum_{x}P(x)log_{2}Q(x) = - \sum_{i=1, k} P(e_{i})log_{2}Q(e_{i})\]

P라는 확률분포에 대해서 Q의 분포의 cross entropy

딥러닝에서 output은 확률값임.
손실함수는 정답(label or target)과 예측값(prediction)을 비교하기 때문에
이를 확률값으로 비교하는 것임.

label 같은 경우도 OHE로 하지만 이것도 1로 되어있는 확률 분포고 output도 확률 분포이기 때문에
이 척도로 비교가능한 것이 바로 CE임.

위의 식을 전개하면,

\[\begin{align}H(P,Q) &= - \sum_{x}P(x)log_{2}Q(x) \\ &= - \sum_{x}P(x)log_{2}P(x) + \sum_{x}P(x)log_{2}P(x) - \sum_{x}P(x)log_{2}Q(x) \\ &= H(P) + \sum_{x}P(x)log_{2}\frac{P(x)}{Q(x)} \\ \end{align}\]

\(- \sum_{x}P(x)log_{2}P(x) + \sum_{x}P(x)log_{2}P(x)\) 이 식을 추가해서 변형한 것임.
이 식을 합치면

\[\begin{align}\sum_{x}P(x)log_{2}P(x) - \sum_{x}P(x)log_{2}Q(x) \\ \Rightarrow \sum_{x}P(x)log_{2}\frac{P(x)}{Q(x)}\end{align}\]

이렇게 되는 데, 이 식을 KL Divergence 라고 함.

여기서 \(P\)를 데이터의 분포라고 하면, 이는 학습과정에서 변화하지 않음.
\(P\)는 고정이기 때문에 \(Q\)를 조정해서 cross entropy값을 최소화 시키는 것임.

Cross Entropy를 손실함수로 사용하는 경우,

\[H(P,Q) = H(P) + \sum_{x}P(x)log_{2}\frac{P(x)}{Q(x)}\]

이 식에서, \(P\)는 고정이기 때문에 KLD를 최소화 하는 것과 동일함.

즉, 가지고 있는 데이터 분포 P(x)와 추정한 데이터 분포 Q(x)간의 차이 최소화 하는데 교차 엔트로피를 사용함.

KLD (Kullback–Leibler divergence)

• P와 Q 사이의 KLD
• 두 확률분포 사이의 거리를 계산할 때 주로 사용.

\[KL(P\Vert Q) = \sum_{x}P(x)log_{2}\frac{P(x)}{Q(x)}\]

P와 Q의 cross entrophy는 p의 엔트로피 + P와 Q간의 KL 다이버전스임.

Logit

DL의 output은 probability가 되어야 하는데,
네트워크를 통과해서 나온 값의 범위는 \(\left[-\infty, \infty \right]\)이기 때문에

activation function(sigmoid)을 적용해서 확률값으로 만들어 주는데, 이런 경우 각 클래스에 대한 확률임 (모든 클래스의 확률을 더했을 때 1이 아님)
multilabel classification일 경우에 가능하지만.
multiclass의 경우에는 모든 클래스에 대한 확률을 원하는 것임(모든 클래스의 확률을 더했을 때 1)
이 역할을 해주는 것이 softmax function임

확률에서의 logit function은 \(log_{e}(\frac{p}{1-p})\) 임.
p가 0%에 가까울 때 logit은 \(-\infty\)이고, 100% 에 가까울 때 logit은 \(\infty\) 임.

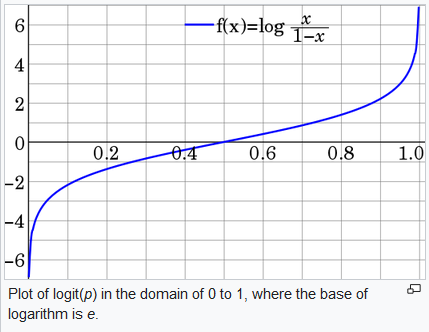
즉 로짓을 가지고 있다면(\(\left[-\infty, \infty \right]\)), 이 범위를 \(\left[0, 1\right]\)로 바꿔줄 수 있다는 의미임.

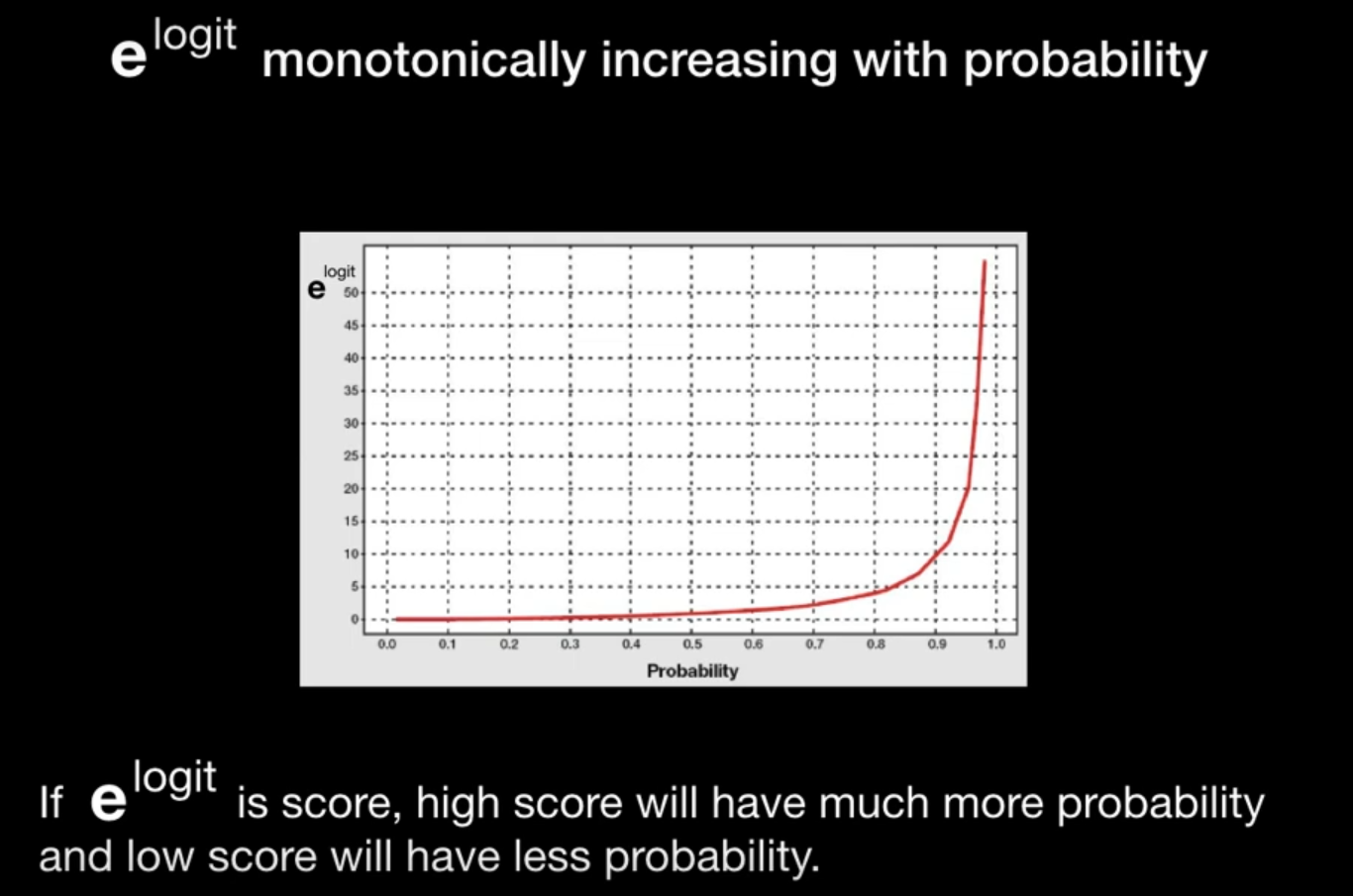
확률이 커지면 로짓도 커지기 때문에 딥러닝에서 확률대신 로짓을 스코어로도 사용이 가능하다는 의미임.

ouput으로 로짓이 나오고 이걸 sigmoid로 바꾸면 각 클래스에 대한 확률이 나옴(모든 클래스에 대해서 각 클래스가 아님, 합하면 1을 넘음)
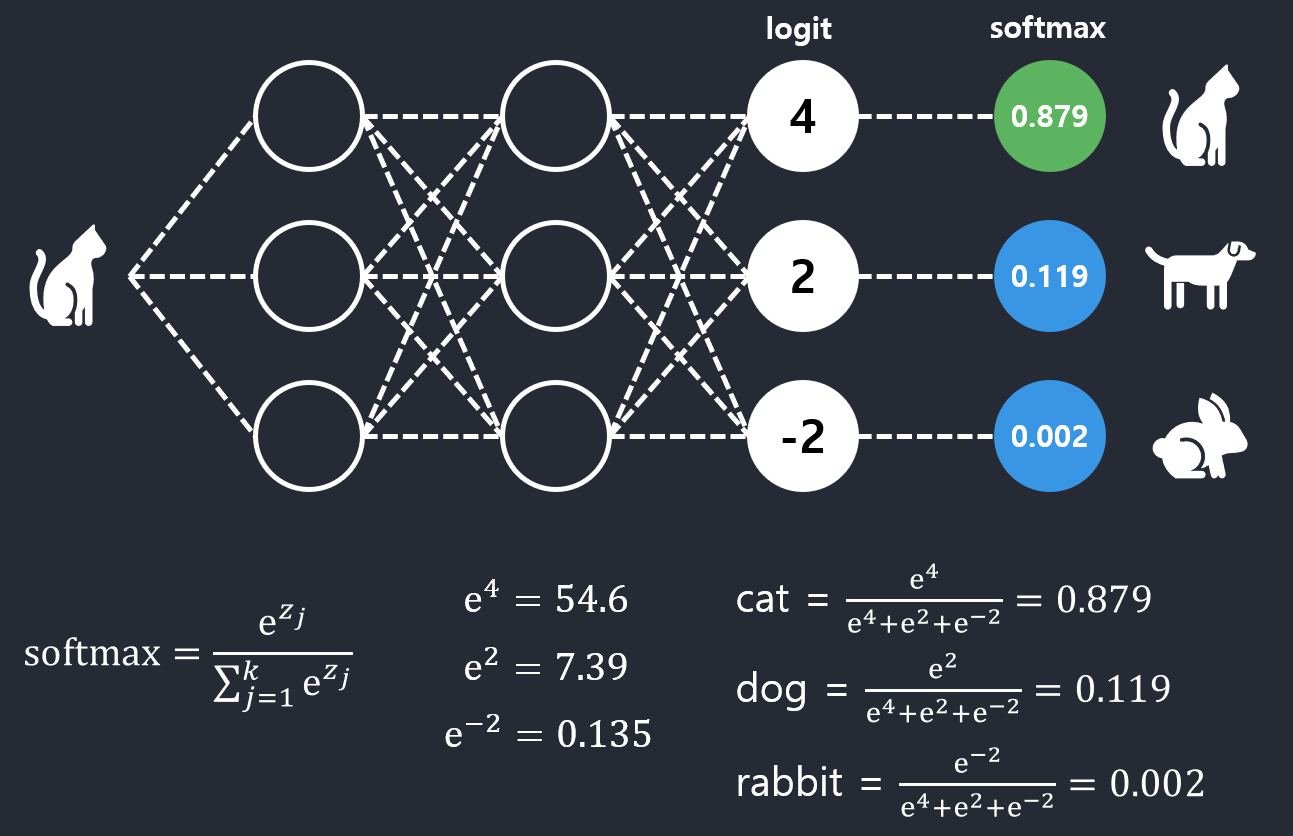
softmax는 로짓을 사용해서 모든 클래스에 대한 확률을 얻게 해줌.
\(e^{logit}\)을 사용함.
\(e^{logit}\) 역시 확률이 커지면 커진다는 성질이 있음.
\(e^{logit}\)을 사용하면 높은 점수는 아주 높게 되고 낮은 점수는 아주 낮게 됨.

이것이 딥러닝에 도움이 되는 이유는 label을 OHE 하기 때문임.
확률값이 높은 것들을 아주 높게, 낮은 값들을 아주 낮게 하면 OHE와 비슷해지기 때문.
따라서 CrossEntropy 학습에 도움이 되는 것임.

why e in log?
0보다 큰 아무 값이나 써도 상관은 없지만(수학적으로는),
딥러닝의 output을 로짓이라고 가정했기 때문에, 로짓은 log에 e base를 사용하고 있음.
따라서, \(e^{logit} = e^{log_{e}(\frac{p}{1-p})} = \frac{p}{1-p}\) 계산이 상당히 간편해짐.
다른 숫자를 사용해도 softmax에 비슷한 결과는 나오지만, 딥러닝 아이디어의 근거가 로짓이기 때문에 e를 사용하는 것임.
오일러 넘버라고 함.

Summary

• Softmax gives probability distribution over predicted output classes.
• The final layer in deep learning has logit values which are raw values for prediction by softmax.
• Logit is the input to softmax

편미분 (partial derivative)

• 변수가 복수인 함수의 미분
• 미분 값이 이루는 벡터를 gradient라고 부름.

Jacobian Matrix

행렬을 미분한 것.
1차 편도 함수

신경망에서 연산은 행렬로 이루어지고, 미분이 필요한데 jacobian을 통해 미분함.

예,

\[\boldsymbol{f}: \mathbb{R}^2 \mapsto \mathbb{R}^3 \ \boldsymbol{f(x)} = (2x_1+x_2^2,\ -x_1^2+3x_2,\ 4x_1x_2)^T\] \[\boldsymbol{J} = \begin{pmatrix} 2 & 2x_2 \\ -2x_1 & 3 \\ 4x_2 & 4x_1 \end{pmatrix}\ \ \ \boldsymbol{J}\vert_{2,1}^{T} = \begin{pmatrix} 2 & 2 \\ -4 & 3 \\ 4 & 8 \end{pmatrix}\]

자코비안이 말하고자 하는 것은 미소 영역에서 ‘비선형 변환’을 ‘선형 변환으로 근사’ 시킨 것.

Appendix

Positive Definite Matrices

Geometric meaning of Determinant

Reference

Manifold Learning: https://deepinsight.tistory.com/124
Representation Learning: https://ratsgo.github.io/deep%20learning/2017/04/25/representationlearning/
Representation Learning: https://velog.io/@tobigs-gnn1213/7.-Graph-Representation-Learning
cs231n slides: http://cs231n.stanford.edu/slides/2021/
SVD: https://darkpgmr.tistory.com/106
logit: https://youtu.be/K7HTd_Zgr3w
partial derivative: https://youtu.be/ly4S0oi3Yz8, https://youtu.be/GkB4vW16QHI, https://youtu.be/AXqhWeUEtQU
jacobian matrix: https://angeloyeo.github.io/2020/07/24/Jacobian.html