ML basics - Probability Distributions 2

가우시안 분포 (Gaussian Distribution)

a single variable \(x\):

\[\mathcal{N}(x \vert \mu, \sigma^2) = \frac{1}{(2\pi \sigma^2)^{1/2}}\exp \left\{ -\frac{1}{2\sigma^2}(x-\mu)^2 \right\}\]

a D-dimensional vector \(\boldsymbol{x}\):

\[\mathcal{N}(\boldsymbol{x} \vert \boldsymbol{\mu}, \Sigma) = \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\exp \left\{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \right\}\]

• \(\boldsymbol{x}\) is a \(D\)-dimensional mean vector.
• \(\Sigma\) is a \(D \times D\) covariance matrix.
• \(\vert \Sigma \vert\) denotes the determinant of \(\Sigma\).

\[\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\exp \left\{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \right\}\]

이 값은 scalar 값이라는 사실을 볼 수 있다.
이유:

• \(\Sigma\)가 행렬이지만 여기서 determinant(\(\vert \Sigma \vert\))을 구했기 때문에.
• 지수부(\(\exp\))는 이차형식이기 때문에 역시 scalar.
  따라서 결과 값은 scalar값이다.

단일변수 \(x\) 이던지 \(D\)차원의 벡터이던지 간에 가우시안 분포가 주어졌을 때 어떤 것이 확률변수이고 확률의 파라미터인지 잘 구분하는 것이 중요하다. \(x\)가 확률변수이고 \(\mu\)와 \(\Sigma\)가 파라미터. 유의할 점은 가우시간 분포가 주어졌을 때, 평균과 분산이 주어진 것이 아니고, 이것들이 파라미터로 주어진 확률밀도 함수의 평균과 공분산이 \(\mu\)와 \(\Sigma(sum)\)이 된다는 것이다.

유의할 점은 가우시간 분포가 주어졌을 때, 평균과 분산이 주어진 것이 아니고, 이것들이 파라미터로 주어진 확률밀도 함수의 평균과 공분산이 \(\boldsymbol{\mu}\)와 \(\Sigma\)이 된다는 것이다.

가우시안 분포가 일어나는 여러가지 상황

1. 정보이론에서 엔트로피를 최대화시키는 확률분포

영상보고 정리할 것

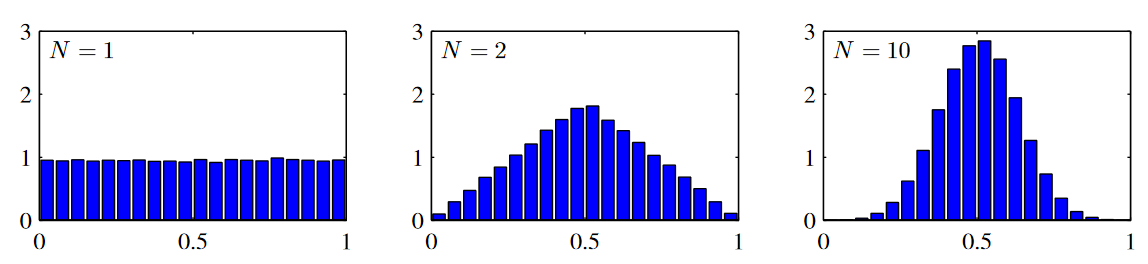
2. 중심극한정리

영상보고 정리할 것

가우시안 분포의 기하학적인 형태

• \(\boldsymbol{x}\)에 대한 함수적 종속성은 지수부에 등장하는 이차형식(quadratic form)에 있다.

\[\Delta^2 = (\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\]

\((\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\) 이러한 형태의 이차형식이 가우시안 분포에서 핵심적인 부분이다.

• \(\Sigma\)가 공분산으로 주어진 것이 아니기 때문에 처음부터 이 행렬이 대칭이라고 생각할 필요는 없다. 하지만 이차형식에 나타나는 행렬은 오직 대칭부분만이 그 값에 기여한다는 사실을 기억하자.

\[x^TAx = (x^TAx)^T = x^TA^Tx = x^T\left( \frac{1}{2}A + \frac{1}{2}A^T \right)x\]

따라서 \(\Sigma\)가 대칭행렬인 것으로 간주할 수 있다.

• 대칭행렬의 성질에 따라서 \(\Sigma\)를 아래와 같이 나타낼 수 있다.

\[\Sigma = U^T\Lambda U\] \[U = \begin{bmatrix} - \boldsymbol u_{1}^{T} - \cr - \boldsymbol u_{2}^{T} - \cr \vdots \cr - \boldsymbol u_{D}^{T} - \end{bmatrix}, \Lambda = diag(\lambda_{1},\cdots,\lambda_{D})\] \[\begin{align} \Sigma &= U^T\Lambda U \\\\ &= \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ \boldsymbol u_{1} &\ \boldsymbol u_{2} &\ \cdots &\ \boldsymbol u_{D}\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} diag(\lambda_{1},\cdots,\lambda_{D}) \begin{bmatrix} - \boldsymbol u_{1}^{T} - \cr - \boldsymbol u_{2}^{T} - \cr \vdots \cr - \boldsymbol u_{D}^{T} - \end{bmatrix} \\\\ &= \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ \boldsymbol u_{1}\lambda_{1} &\ \boldsymbol u_{2}\lambda_{2} &\ \cdots &\ \boldsymbol u_{D}\lambda_{D}\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} \begin{bmatrix} - \boldsymbol u_{1}^{T} - \cr - \boldsymbol u_{2}^{T} - \cr \vdots \cr - \boldsymbol u_{D}^{T} - \end{bmatrix} \\\\ &= \sum_{i=1}^{D}\lambda_{i}\boldsymbol u_{i}\boldsymbol u_{i}^{T} \end{align}\]

• \(\Sigma^{-1}\)도 쉽게 구할 수 있다.

\[\Sigma^{-1} = \sum_{i=1}^{D}\frac{1}{\lambda_{i}}\boldsymbol u_{i}\boldsymbol u_{i}^{T}\]

• 이차형식은 다음과 같이 표현될 수 있다.

\[\Delta^2 = \sum_{i=1}^{D}\frac{y_{i}^2}{\lambda_{i}}\] \[y_{i} = \boldsymbol u_{i}^{T}(\boldsymbol{x} - \boldsymbol \mu)\]

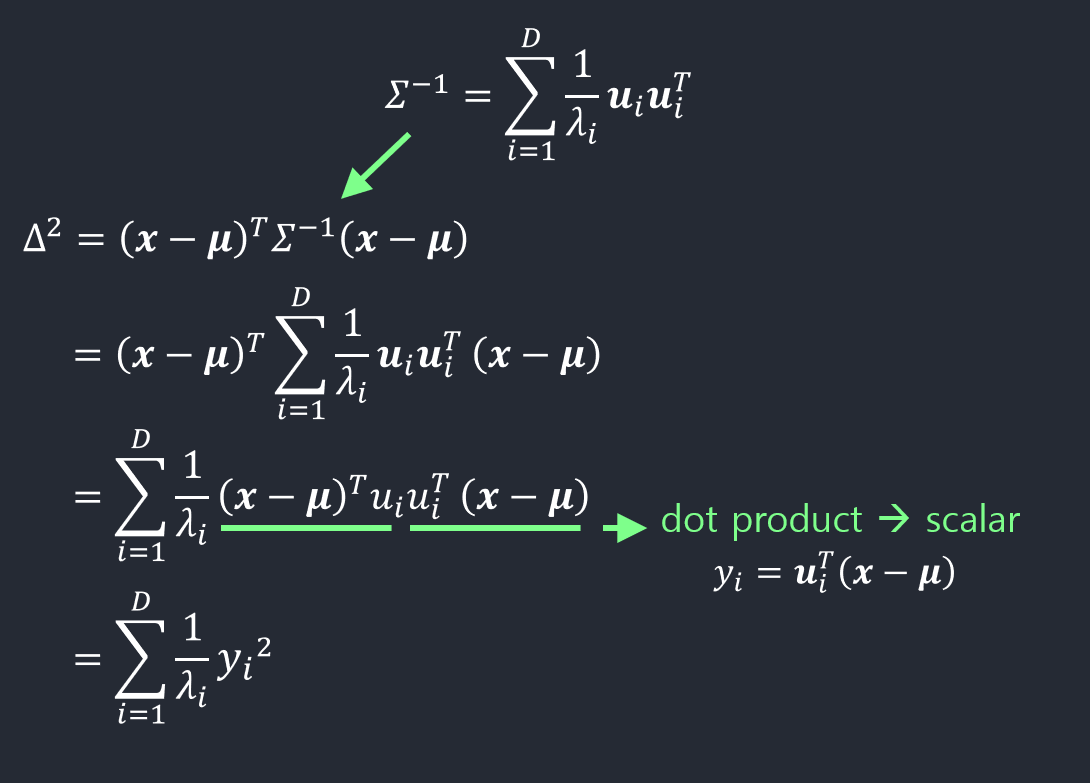
• 벡터식으로 확장하면

\[\boldsymbol y = U(\boldsymbol{x} - \boldsymbol \mu)\]

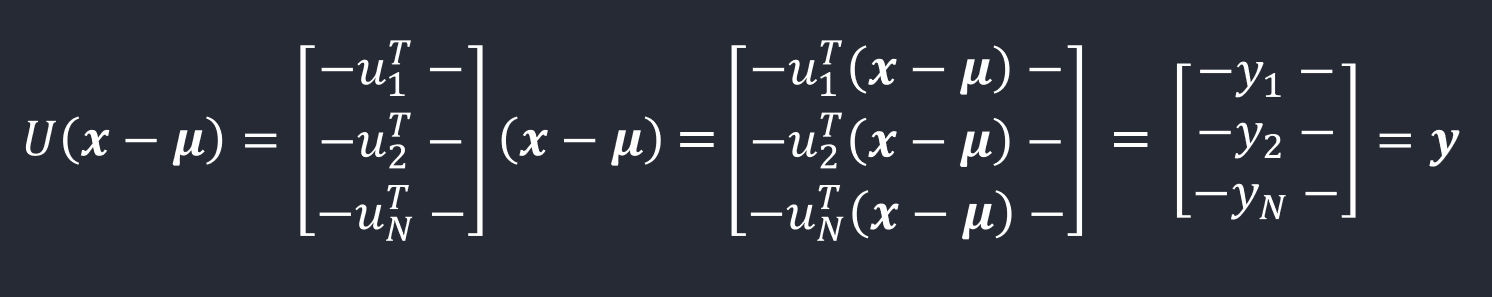
• \(\boldsymbol y\)를 벡터들 \(\boldsymbol \mu_{i}\)에 의해 정의된 새로운 좌표체계 내의 점으로 해석할 수 있다. 이것을 기저변환(change of basis)이라고 한다.

\[\begin{align} \boldsymbol y &= U(\boldsymbol{x} - \boldsymbol \mu) \\ \boldsymbol{x} - \boldsymbol \mu &= U^{-1}\boldsymbol y \\ &= U^{T}\boldsymbol y \\ &= \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ \boldsymbol u_{1} &\ \boldsymbol u_{2} &\ \cdots &\ \boldsymbol u_{D}\\ \vert &\ \vert &\ &\ \vert \end{bmatrix}\boldsymbol y \end{align}\]

• \(\boldsymbol{x} - \boldsymbol \mu\): standard basis에서의 좌표
• \(\boldsymbol y\): basis \(\{\boldsymbol u_{1}, \boldsymbol u_{2}, \cdots, \boldsymbol u_{D} \}\)에서의 좌표

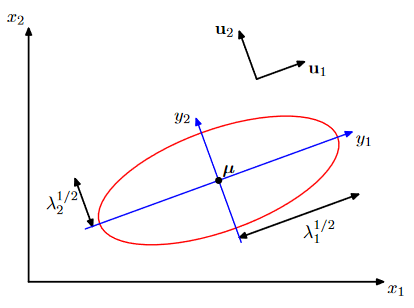
\(\boldsymbol{y}\)는 coefficient들을 모아논 값.
red circle: x1, x2 좌표내에서 점들의 집합이 동일한 분포를 갖는다.
고유벡터 \(u_1 \sim u_d\)까지를 basis로 하는 좌표계에서는 차원을 이루고 그 모양은 고유값들에 의해 결정된다.

가우시안 분포의 Normalization 증명

• 확률이론시간에 배운 확률변수의 함수를 복습하라. \(\boldsymbol y\)의 확률밀도함수를 구하기 위해서 Jacobian \(\boldsymbol J\)를 구해야 한다.

\[J_{ij} = \frac{\partial x_{i}}{\partial y_{i}} = U_{ij} = (U^{T})_{ij}\]

결국 \(\boldsymbol J = U^T\)라는 사실을 알 수 있다.

\[\vert \boldsymbol J \vert ^2 = \vert U^T\vert ^2 = \vert U^T\vert\vert U\vert = \vert U^{T}U\vert = \vert \boldsymbol I\vert = 1\]

• 행렬식 \(\vert \Sigma\vert\)는 고유값의 곱으로 나타낼 수 있다.

\[\vert \Sigma\vert^{1/2} = \prod_{j=1}^{D} \lambda_{i}^{1/2}\]

• 따라서, \(\boldsymbol y\)의 확률밀도함수는

\[p(\boldsymbol y) = p(\boldsymbol{x})\vert \boldsymbol J\vert = \prod_{j=1}^{D}\frac{1}{(2\pi\lambda_{j})^{1/2}}\exp\left\{ -\frac{y_{j}^{2}}{2\lambda_{j}} \right\}\]

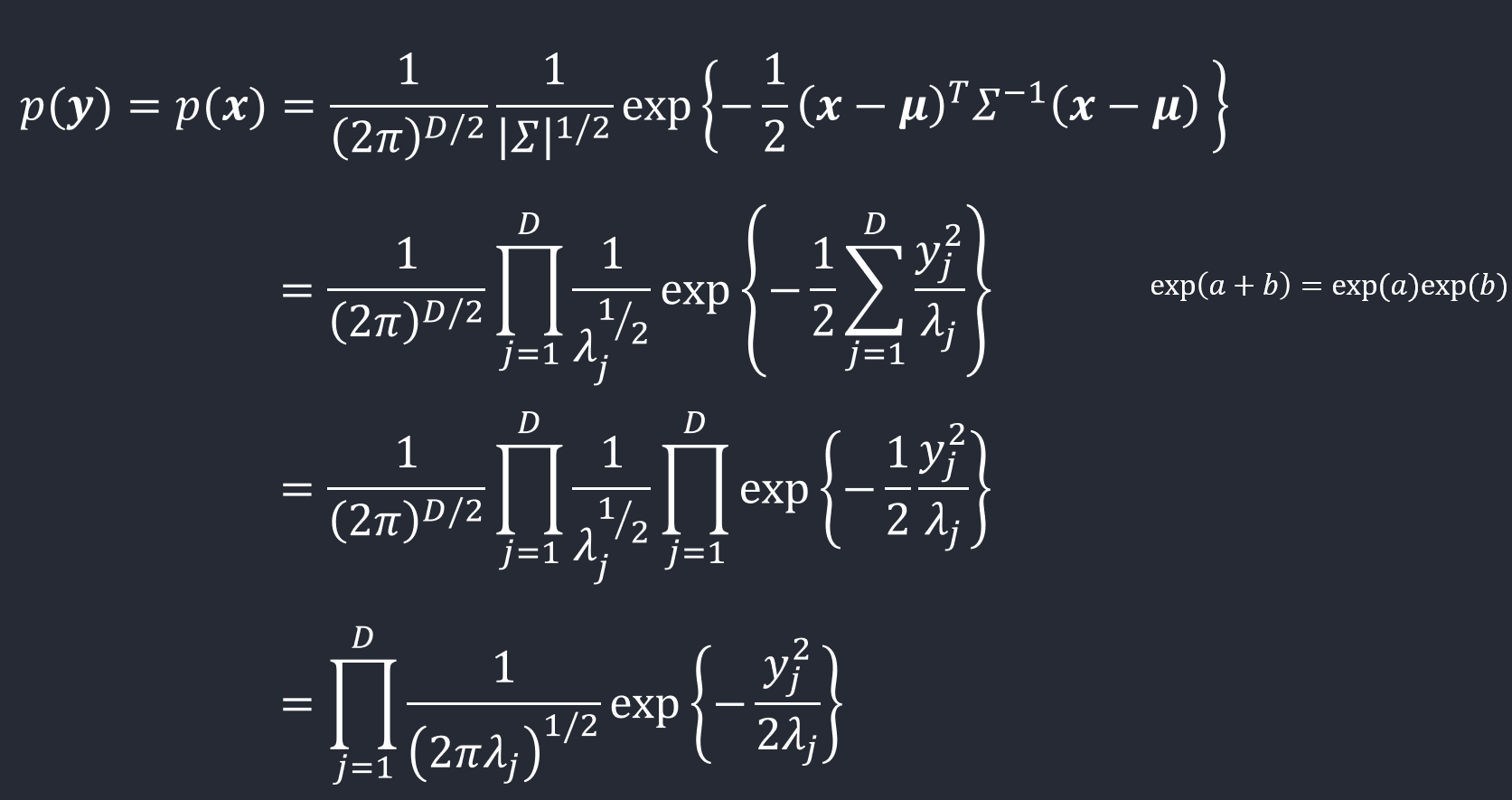
• \(\boldsymbol y\)의 normalization

\[\int p(\boldsymbol y)d\boldsymbol y = \prod_{j=1}^{D}\int_{-\infty}^{\infty}\frac{1}{(2\pi\lambda_{j})^{1/2}}\exp\left\{ -\frac{y_{j}^{2}}{2\lambda_{j}} \right\}dy_{j}=1\]

적분을 하게 되면 D개의 y variables이 각각 다른 변수들이기 때문에 D개의 적분의 곱으로 나타낼 수 있다.
따라서단일변수의 가우시안 분포와 같다. 이미 단일 변수일 경우 normalize되었다는 것을 확인했기 때문에 이를 D번 곱해주는 결과와 같게 된다.

가우시안 분포의 기댓값

\(\mu\)와 \(\Sigma\)가 정의된 것이 아니라 단순히 함수의 파라미터로 주어져있는데 기댓값과 공분산의 정의를 통해 식을 유도하다 보면 \(\mu\)와 \(\Sigma\)가 가지는 의미를 찾을 수 있게 될 것이다. 결국 \(\mu\)가 확률분포의 기댓값이 되고 \(\Sigma\)가 확률분포의 공분산이 될 것임

다변량(multivariate) 확률변수의 기댓값

• \(\boldsymbol{x} = (x_{1},\cdots,x_{n})^T\)
• \(\mathbb{E}[\boldsymbol{x}] = (\mathbb{E}[x_{1}],\cdots,\mathbb{E}[x_{n}])^T\)
• \(\mathbb{E}[x_{1}] = \int x_{1}p(x_1)dx_1 = \int x_1 (\int p(x_1, \cdots, x_n)dx_2, \cdots, dx_n)dx_1 = \int x_1 p(x_1,\cdots,x_n)dx_1, \cdots, dx_n\)

\(\boldsymbol{x}\)가 벡터일 때 \(\boldsymbol{x}\)의 기댓값도 벡터가 된다.
\(\boldsymbol{x}_{1}\)의 기댓값을 정의했을 때, \(x_{1}\)에 \(p(x_1)\)을 곱한 값을 적분한 값이 된다. \(\int x_{1}p(x_1)dx_1\)
\(p(x_1)\)이라는 것은 marginalization(주변화)를 통해서 구할 수 있을 것이다.
\(\int p(x_1, \cdots, x_n)dx_2, \cdots, dx_n\) : joint probability의 pdf \(p(x_1, \cdots, x_n)\)가 주어졌을 때 \(x_{1}\)을 제외한 나머지 모든 값들에 대해 적분을 하게 되면 주변화를 통해 \(p(x_1)\)의 값이 구해지게 되는 것이다.
정리하면, \(x_1\)에 joint probability의 pdf( \(p(x_1, \cdots, x_n)\) )를 곱하고 \(x_1,\cdots,x_n\)까지 모든 변수에 대해 적분을 하면 \(x_{1}\)의 기댓값이 된다.

\[\mathbb{E}[\boldsymbol{x}] = \int p(\boldsymbol{x})\boldsymbol{x}d\boldsymbol{x}\]

가우시안 분포의 기댓값

\[\begin{align} \mathbb{E}[\boldsymbol{x}] &= \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \right\}\boldsymbol{x} d \boldsymbol{x} \\\\ &= \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}\boldsymbol{z}^T\Sigma^{-1}\boldsymbol{z} \right\}(\boldsymbol{z} + \boldsymbol \mu)d\boldsymbol{z} &\ \mathrm{by}~ \boldsymbol{z} = \boldsymbol{x}-\boldsymbol{\mu} \end{align}\]

\(\boldsymbol{z}\)와 \(\boldsymbol{\mu\) 부분을 고려하면 된다.

\(\boldsymbol{z}\)에 관한 적분:
지수함수를 포함한 부분이 odd function이기 때문에 결국 적분의 결과 값은 0이 된다.

\[\begin{align} \int \exp \left\{ -\frac{1}{2}\boldsymbol{z}^T\Sigma^{-1}\boldsymbol{z} \right\}\boldsymbol{z}d\boldsymbol{z} &= \int\vert \boldsymbol J\vert \exp \left\{ -\frac{1}{2} \sum_{i=1}^{D} \frac{y_{i}^{2}}{\lambda_{i}} \right\}\boldsymbol{y}d\boldsymbol{y} &\ \mathrm{by}~ \boldsymbol{z} = \sum_{j=1}^{D}y_{j}\boldsymbol{u}_{j}, y_{j} = \boldsymbol{U}_{j}^{T}\boldsymbol{z}\\\\ &= \begin{bmatrix} \int \exp\left\{ -\frac{1}{2}\sum_{i=1}^{D}\frac{y_{i}^{2}}{\lambda_{i}}y_{1}dy_{1},\cdots,dy_{D} \right\} \cr \int \exp\left\{ -\frac{1}{2}\sum_{i=1}^{D}\frac{y_{i}^{2}}{\lambda_{i}}y_{D}dy_{1},\cdots,dy_{D} \right\} \end{bmatrix} \end{align}\] \[\begin{align} \int \exp\left\{ -\frac{1}{2}\sum_{i=1}^{D}\frac{y_{i}^{2}}{\lambda_{i}}\right\}y_{1}dy_{1},\cdots,dy_{D} &= \int\left( \int_{0}^{\infty}\exp\left\{ -\frac{1}{2}\sum_{i=1}^{D}\frac{y_{i}^{2}}{\lambda_{i}}\right\}y_{1}dy_{1} + \int_{-\infty}^{0}\exp\left\{ -\frac{1}{2}\sum_{i=1}^{D}\frac{y_{i}^{2}}{\lambda_{i}}\right\}y_{1}dy_{1} \right)dy_{2}\cdots dy_{D} \\\\ &= \int\left( \int_{0}^{\infty}\exp\left\{ -\frac{1}{2}\sum_{i=1}^{D}\frac{y_{i}^{2}}{\lambda_{i}}\right\}y_{1}dy_{1} + \int_{0}^{\infty}\exp\left\{ -\frac{1}{2}\sum_{i=1}^{D}\frac{y_{i}^{2}}{\lambda_{i}}\right\}(-y_{1})dy_{1} \right)dy_{2}\cdots dy_{D} \\\\ &= 0 \end{align}\]

남은 \(\boldsymbol{\mu}\) 부분은 \(\boldsymbol{z}\)와는 독립적이기 때문에 위의 적분식 바깥으로 나갈 수 있다.

\(\boldsymbol{\mu}\)가 나가고 남는 부분은 기본적인 가우시안 분포이기 때문에 적분을 하게 되면 1이 된다.

따라서 \(\boldsymbol{\mu} \times 1\)이 되기 때문에,

\[\mathbb{E}[\boldsymbol{x}] = \boldsymbol \mu\]

가우시안 분포의 공분산

공분산을 구하기 위해서 먼저 2차 적률(second order moments)을 구한다.

2차 적률: 단일변수일 경우 제곱의 기댓갑을 의미하고, 벡터일 경우 \(xx^T\)의 기댓값을 의미한다.

예를 들어, x가 2차원일 경우:

\(\boldsymbol{x} = \begin{bmatrix} {x}_{1} \cr {x}_{2} \end{bmatrix}\) 이고,

\(\boldsymbol{x}\boldsymbol{x}^{T}\)는 외적이 되기 때문에 여전히 행렬이다.

\(\begin{align}\mathbb{E}[\boldsymbol{x}\boldsymbol{x}^{T}] &= \int p(x_1, x_2)\boldsymbol{x}\boldsymbol{x}^{T}d\boldsymbol{x}_{1}d\boldsymbol{x}_{2} \\ &= \int p(x_1, x_2) \begin{bmatrix} {x}_{1}{x}_{1} & {x}_{1}{x}_{2} \cr {x}_{2}{x}_{1} & {x}_{2}{x}_{2} \end{bmatrix}d\boldsymbol{x}_{1}d\boldsymbol{x}_{2} \\ &= \begin{bmatrix} \int p(x_{1}, x_{2})x_{1}x_{1}d\boldsymbol{x}_{1}d\boldsymbol{x}_{2} & \int p(x_{1}, x_{2})x_{1}x_{2}d\boldsymbol{x}_{1}d\boldsymbol{x}_{2} \cr \int p(x_{1}, x_{2})x_{2}x_{1}d\boldsymbol{x}_{1}d\boldsymbol{x}_{2} & \int p(x_{1}, x_{2})x_{2}x_{2}d\boldsymbol{x}_{1}d\boldsymbol{x}_{2} \end{bmatrix} \end{align}\)

\[\begin{align} \mathbb{E}[\boldsymbol{x}\boldsymbol{x}^{T}] &= \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \right\}\boldsymbol{x}\boldsymbol{x}^{T} d \boldsymbol{x} \\\\ &= \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}\boldsymbol{z}^T\Sigma^{-1}\boldsymbol{z} \right\}(\boldsymbol{z} + \boldsymbol{\mu})(\boldsymbol{z} + \boldsymbol{\mu})^{T}d\boldsymbol{z} \end{align}\]

\(\mathbb{E}[\boldsymbol{x}\boldsymbol{x}^{T}]\)는 \(D \times D\) 행렬임을 기억하라. \(\boldsymbol{z}\)를 \(U^{T}\boldsymbol y\)로 치환하면

\[\boldsymbol{z} = U^{T}\boldsymbol{y} = \begin{bmatrix} \vert &\ \cr \boldsymbol{u}_{1} &\ \cdots \cr \vert &\ \end{bmatrix}\boldsymbol{y} = \Sigma\boldsymbol{u}_{i}y_{i}\] \[\boldsymbol{z}\boldsymbol{z}^{T} = (\Sigma\boldsymbol{u}_{i}y_{i})(\Sigma\boldsymbol{u}_{j}^{T}y_{j}) = \Sigma_{i}\Sigma_{j}\boldsymbol{u}\boldsymbol{u}_{j}^{T}y_{i}y_{j}\]

이러한 이차형식을 y에 관한 합의 형태로 나타낼 수 있다.
\(\boldsymbol{z}\Sigma^{-1}\boldsymbol{z}^{T} = (U^{T}\boldsymbol{y})^{T}\Sigma^{-1}(U^{T}\boldsymbol{y}) = (\boldsymbol{y}^{T}U)(U^{T}\Lambda{-1}U)(U^{T}\boldsymbol{y}) = \boldsymbol{y}^{T}\Lambda^{-1}\boldsymbol{y} = \Sigma_{i=1}^{D}\Sigma_{j=1}^{D}\Lambda_{ij}^{-1}y_{i}y_{j} = \Sigma_{i=1}^{D}\frac{1}{\Lambda_{i}}y_{i}^{2}\)

\(\Sigma^{-1} = U^{T}\Lambda{-1}U\)를 활용.
\(\Lambda_{ij}^{-1}\)이 대각행렬이기 때문에 남는 부분은 대각선 원소이다.

\[\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}\boldsymbol{z}^T\Sigma^{-1}\boldsymbol{z} \right\}\boldsymbol{z}\boldsymbol{z}^{T}d\boldsymbol{z} = \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\sum_{i=1}^{D}\sum_{j=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T} \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}y_{j}d\boldsymbol{y}\]

\(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}\boldsymbol{z}^T\Sigma^{-1}\boldsymbol{z} \right\}\boldsymbol{z}\boldsymbol{z}^{T}d\boldsymbol{z}\) 이 적분은 하나의 행렬이다. \(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\sum_{i=1}^{D}\sum_{j=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T} \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}y_{j}d\boldsymbol{y}\) 이 부분은 행렬들을 계속 더한 부분이다. \(\sum_{i=1}^{D}\sum_{j=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T}\) \(D\times D\)개의 개수만큼 행렬을 더한 것이다. \(D\times D\)개의 행렬중에서 \(i\neq j\)인 모든 경우에 그 행렬들이 영행렬이 된다는 사실이다.

행렬 \(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\sum_{i=1}^{D}\sum_{j=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T} \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}y_{j}d\boldsymbol{y}\)은 \(D^2\)개의 행렬의 합인데 그 중 \(i \neq j\)인 모든 경우 영행렬이 된다.

\(\int^{i \neq j} \cdots \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}y_{j}d\boldsymbol{y} = \int \cdots y_{i}\left[ \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}dy_{i} \right]d\boldsymbol{y}\setminus \{y_{i}\}\)
\(= 0\)

위 식에서 \(y_i\)에 대해 적분을 하게 되면 \(y_j\)는 앞으로 나가게 되고, \(\left[ \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}dy_{i} \right]\) 이 부분은 odd function이 된다. 따라서 0이 되기 때문에 전체가 0이 되는 것이다.

\(\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\sum_{i=1}^{D}\sum_{j=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T} \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}y_{j}d\boldsymbol{y}\) 이것은 행렬들의 합이라고 했는데, 그 합들 중에서 살아남는 부분은 \(i = j\) 일때만 살아남게 되는 것이다.

따라서,

아래의 식에서 summation이 두개 (\(\sum_{i=1}^{D}\sum_{j=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T}\))가 있었지만 i=j일 경우에만 있으면 되기 때문에 \(\sum_{i=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T}\)로 변환한다.

합의 형태로 된 지수부 \(\exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}\)를 곱의 형태로 바꿔준다.

\(\left[ \prod_{k=\{1,\cdots,D\}\setminus\{i\}} \int \exp \left\{ -\frac{1}{2}\frac{y_{k}^{2}}{\lambda_{k}} \right\}dy_{k} \right]\) 이 부분은 1이 될 것이고, \(\left[ \int\exp\left\{ -\frac{1}{2}\frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}^{2}dy_{i} \right]\) 이 부분도 단일변수의 성질을 이용해서 \(\lambda_i\)가 된다.

\[\begin{align} \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\sum_{i=1}^{D}\sum_{j=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{j}^{T} \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}y_{j}d\boldsymbol{y} &= \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\sum_{i=1}^{D}\sum_{i=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{i}^{T} \int \exp \left\{ -\frac{1}{2} \sum_{k=1}^{D} \frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}^{2}d\boldsymbol{y} \\ &= \sum_{i=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{i}^{T} \left[ \frac{1}{(2\pi)^{D/2}}\prod_{j=1}^{D}\frac{1}{\lambda_{j}^{1/2}} \right]\left[ \prod_{k=\{1,\cdots,D\}\setminus\{i\}} \int \exp \left\{ -\frac{1}{2}\frac{y_{k}^{2}}{\lambda_{k}} \right\}dy_{k} \right]\left[ \int\exp\left\{ -\frac{1}{2}\frac{y_{k}^{2}}{\lambda_{k}} \right\}y_{i}^{2}dy_{i} \right] \\\\ &= \sum_{i=1}^{D}\boldsymbol{u}_{i}\boldsymbol{u}_{i}^{T}\lambda_{i}\\\\ &= \Sigma \end{align}\]

\({k=\{1,\cdots,D\}\setminus\{i\}}\): set - set의 의미이다. 따라서 k가 1부터 D까지 중에서 i가 아닌 모든 경우에 대해서.

\[\mathbb{E}[\boldsymbol{x}\boldsymbol{x}^{T}] = \boldsymbol{\mu}\boldsymbol{\mu}^{T} + \Sigma\]

\(\begin{align} \mathbb{E}[\boldsymbol{x}\boldsymbol{x}^{T}] &= \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \right\}\boldsymbol{x}\boldsymbol{x}^{T} d \boldsymbol{x} \\\\ &= \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert \Sigma \vert^{1/2}}\int \exp \left\{ -\frac{1}{2}\boldsymbol{z}^T\Sigma^{-1}\boldsymbol{z} \right\}(\boldsymbol{z} + \boldsymbol{\mu})(\boldsymbol{z} + \boldsymbol{\mu})^{T}d\boldsymbol{z} \end{align}\) 이 식에서,
\(\boldsymbol{z}\boldsymbol{z}^{T}\)와 관련된 부분이 \(\Sigma\)가 됨을 보였고, \(\boldsymbol{z} \times \boldsymbol{\mu}^{T}\) 부분, \(\boldsymbol{\mu} \times \boldsymbol{z}^{T}\) 부분, \(\boldsymbol{\mu} \times \boldsymbol{\mu}^{T}\) 부분을 안했지만, \(\boldsymbol{z} \times \boldsymbol{\mu}^{T}\) 이것은 기댓값을 할때 odd function을 사용해서 사라지게 되고, \(\boldsymbol{\mu} \times \boldsymbol{\mu}^{T}\)만 남게 되는데, 앞에 있는 \(\left\{ -\frac{1}{2}\boldsymbol{z}^T\Sigma^{-1}\boldsymbol{z} \right\}\)에 대해서는 별개이기 때문에 적분앞으로 나가서 결과적으로 \(\boldsymbol{\mu}\boldsymbol{\mu}^{T}\)만 남게 되는 것이다.

결과적으로

\[\mathbb{E}[\boldsymbol{x}\boldsymbol{x}^{T}] = \boldsymbol{\mu}\boldsymbol{\mu}^{T} + \Sigma\]

이 식이 완성된다.

확률변수의 벡터 \(\boldsymbol{x}\)를 위한 공분산은 다음과 같이 정의된다.

\[cov[\boldsymbol{x}] = \mathbb{E}[(\boldsymbol{x}-\mathbb{E}[\boldsymbol{x}])(\boldsymbol{x}-\mathbb{E}[\boldsymbol{x}])^{T}]\]

위의 결과를 이용하면 공분산은

\[cov[\boldsymbol{x}] = \Sigma\]

확률변수 벡터 \(x\)가 가우시안 분포를 따를 때, 그 분포의 파라미터로 주어져 있던 \(\mu\)가 바로 그 분포의 평균이 되고, 파라미터로 주어져 있던 \(\Sigma\)가 공분산이 된다는 사실을 알게 됨.

조건부 가우시안 분포 (Conditional Gaussian Distribution)

\(D\)차원의 확률변수 벡터 \(\boldsymbol{x}\)가 가우시안 분포 \(\mathcal{N}(\boldsymbol{x} \vert \boldsymbol{\mu}, \sigma)\)를 따른다고 하자. \(\boldsymbol{x}\)를 두 그룹의 확률변수들로 나누었을 때, 한 그룹이 주어졌을 때 나머지 그룹의 조건부 확률도 가우시안 분포를 따르고, 각 그룹의 주변확률 또한 가우시안 분포를 따른다는 것을 보이고자 한다.

\(\boldsymbol{x}\)가 다음과 같은 형태를 가진다고 하자.

\[\boldsymbol{x} = \begin{bmatrix} \boldsymbol{x}_{a} \cr \boldsymbol{x}_{b} \end{bmatrix}\]

\(\boldsymbol{x}_{a}\)는 \(M\)개의 원소를 가진다고 하자. 그리고 평균 벡터와 공분산 행렬은 다음과 같이 주어진다고 하자.

\(\boldsymbol{x}_{a}\)는 \(M\)개의 원소를 가진다고 했기 때문에, \(\boldsymbol{x}_{b}\)는 \(D-M\)개의 원소를 가진다.

\[\boldsymbol{\mu} = \begin{bmatrix} \boldsymbol{\mu}_{a} \cr \boldsymbol{\mu}_{b} \end{bmatrix}\] \[\Sigma = \begin{bmatrix} \Sigma_{aa} & \Sigma_{ab} \cr \Sigma_{ba} & \Sigma_{bb} \end{bmatrix}\]

때로는 공분산의 역행렬, 즉 정확도 행렬(precision matrix)을 사용하는 것이 수식을 간편하게 한다.

\[\Lambda = \Sigma^{-1}\] \[\Lambda = \begin{bmatrix} \Lambda_{aa} & \Lambda_{ab} \cr \Lambda_{ba} & \Lambda_{bb} \end{bmatrix}\]

\(\Sigma\)와 \(\Lambda\)는 symmetric 이다. 따라서 \(\Sigma_{ab}^{T} = \Sigma_{ba}\)이고 \(\Lambda_{ab}^{T} = \Lambda_{ba}\)

\(\Lambda = \Sigma^{-1}\)라고 해서 각각의 작은 행렬들에 대해서는 성립하지 않는다. 따라서, \(\Sigma_{aa}^{-1}\neq \Lambda_{aa}\)이다.

지수부의 이차형식을 위의 파티션을 사용해서 전개해보자.

\[\boldsymbol{z} = \begin{bmatrix} \boldsymbol{x}_{a} \cr \boldsymbol{x}_{b} \end{bmatrix} - \begin{bmatrix} \boldsymbol{\mu}_{a} \cr \boldsymbol{\mu}_{b} \end{bmatrix} = \begin{bmatrix} \boldsymbol{z}_{a} \cr \boldsymbol{z}_{b} \end{bmatrix}\] \[\boldsymbol{z}^{T}\Lambda\boldsymbol{z} = \boldsymbol{z}^{T} \begin{bmatrix} \Lambda_{aa} & \Lambda_{ab} \cr \Lambda_{ba} & \Lambda_{bb} \end{bmatrix} = \begin{bmatrix} \boldsymbol{z}^{T} \begin{bmatrix} \Lambda_{aa} \cr \Lambda_{ba} \end{bmatrix} & \boldsymbol{z}^{T} \begin{bmatrix} \Lambda_{ab} \cr \Lambda_{bb} \end{bmatrix} \end{bmatrix}\boldsymbol{z}\]

여기서 사이즈를 먼저 확인하자. \(\boldsymbol{z}^{T} \begin{bmatrix} \Lambda_{aa} \cr \Lambda_{ba} \end{bmatrix}\) 이것은 \(1\times M\)이고 \(\boldsymbol{z}^{T} \begin{bmatrix} \Lambda_{ab} \cr \Lambda_{bb} \end{bmatrix}\) 이것은 \(1\times (D-M)\)이다.

\[= \begin{bmatrix} \boldsymbol{z}_{a}^{T}\Lambda_{aa} + \boldsymbol{z}_{b}^{T}\Lambda_{ba} & \boldsymbol{z}_{a}^{T}\Lambda_{ab} + \boldsymbol{z}_{b}^{T}\Lambda_{bb} \end{bmatrix}\boldsymbol{z}\] \[= \boldsymbol{z}_{a}^{T}\Lambda_{aa}\boldsymbol{z}_{a} + \boldsymbol{z}_{b}^{T}\Lambda_{ba}\boldsymbol{z}_{a} + \boldsymbol{z}_{a}^{T}\Lambda_{ab}\boldsymbol{z}_{b} + \boldsymbol{z}_{b}^{T}\Lambda_{bb}\boldsymbol{z}_{b}\]

따라서 위에서 \(\boldsymbol{z}\)에 관해서 정의한 것을 다시 \(x\)와 \(\mu\)에 대한 관계식으로 넣어준다면, \(\boldsymbol{z}_{a} = (\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})\)가 되기 때문에 이 식을 아래처럼 바꿔줄 수 있는 것이다.

\[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\] \[= -\frac{1}{2}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})^{T}\Lambda_{aa}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})-\frac{1}{2}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})^{T}\Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\\\\ -\frac{1}{2}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})^{T}\Lambda_{ba}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})-\frac{1}{2}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})^{T}\Lambda_{bb}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\]

\(\boldsymbol{x}_{a}\)에 대한 조건부 확률을 구할 준비가 되었다.

\(\boldsymbol{x}_{b}\)가 주어졌을 때 \(\boldsymbol{x}_{a}\)의 조건부확률 (\(p(\boldsymbol{x}_{a}\vert \boldsymbol{x}_{b})\))을 구하는 것이다.

완전제곱식 (Completing the Square) 방법

단일 변수일 경우, \(x^2-ax + (\frac{a}{2})^2 - (\frac{a}{2})^2 = (x-\frac{a}{2})^2 - (\frac{a}{2})^2\) 이렇게 되는 것이 완전 제곱식이다.

완전제곱식을 사용해서 곱의 형태로 나타내기 위해서 사용한다.

확률밀도함수 \(p(\boldsymbol{x}_{a}, \boldsymbol{x}_{b})\)를 \(p(\boldsymbol{x}_{a}, \boldsymbol{x}_{b}) = g(\boldsymbol{x}_{a}\alpha)\)로 나타낼 수 있다고 하자. 여기서 \(\alpha\)는 \(\boldsymbol{x}_{a}\)와 독립적이고 \(\int g(\boldsymbol{x}_{a})d\boldsymbol{x}_{a}=1\)이다. 따라서

\[\begin{align} \int p(\boldsymbol{x}_{a}, \boldsymbol{x}_{b})d\boldsymbol{x}_{a} &= \int g(\boldsymbol{x}_{a})\alpha d\boldsymbol{x}_{a} \\ &= \alpha \int g(\boldsymbol{x}_{a}) d\boldsymbol{x}_{a} \\ &= \alpha \end{align}\] \[\alpha = p(\boldsymbol{x}_{b})\]

\(\alpha\)는 위의 식에서 \(\boldsymbol{x}_{a}\)에 대해 적분했기 때문에 결과적으로 \(p(\boldsymbol{x}_{b})\)라는 \(\boldsymbol{x}_{b}\)의 주변확률이 되는 것이다.

\[p(\boldsymbol{x}_{a}, \boldsymbol{x}_{b}) = g(\boldsymbol{x}_{a})p(\boldsymbol{x}_{b})\]

이것을 다시 원래의 식에 대입을 해보면 \(g(\boldsymbol{x}_{a})p(\boldsymbol{x}_{b})\)가 되는 것이다.

\[g(\boldsymbol{x}_{a}) = p(\boldsymbol{x}_{a}\vert \boldsymbol{x}_{b})\]

따라서 \(g(\boldsymbol{x}_{a})\)는 결국 조건부확률이 되는 것이다.

위 과정을 통해 원래의 결합확률 분포를 변형시켜서 함수 \(g(\boldsymbol{x}_{a})\)를 찾는 것이 목표이다.

---

이차형식과 완전제곱식의 관계

\(\tau\)를 사용해서

\(-\frac{1}{2}\boldsymbol{x}_{a}^{T}A\boldsymbol{x}_{a} + \boldsymbol{x}_{a}^{T}m = -\frac{1}{2}\boldsymbol{x}_{a}^{T}A\boldsymbol{x}_{a} + \boldsymbol{x}_{a}^{T}m - \tau + \tau\)
\(= -\frac{1}{2}(\boldsymbol{x}_{a} - ?)^{T}A(\boldsymbol{x}_{a} - ?) + \tau\)
\(p(\boldsymbol{x}_{a},\boldsymbol{x}_{b}) = a\exp\{ -\frac{1}{2}(\boldsymbol{x}_{a} - ?)^{T}\Lambda_{aa}(\boldsymbol{x}_{a} - ?) \}\exp\{\tau\}\)

\(\boldsymbol{x}_{a}\)관한 분포함수를 normalize 시키기 위해 상수\(b\)를 구하게 되면

\[= b\exp\{ -\frac{1}{2}(\boldsymbol{x}_{a} - ?)^{T}\Lambda_{aa}(\boldsymbol{x}_{a} - ?) \}\frac{a}{b}\exp\{\tau\}\]

\(b\exp\{ -\frac{1}{2}(\boldsymbol{x}_{a} - ?)^{T}\Lambda_{aa}(\boldsymbol{x}_{a} - ?) \}\) 이 부분을 \(g(\boldsymbol{x}_{a})\)라고 볼 수 있고, 나머지 \(\frac{a}{b}\exp\{\tau\}\)를 \(\alpha\)라고 볼 수 있다.

이처럼, 주어진 가우시안 분포함수를 변형시켜서 조건부확률을 구할 수 있게 되는 것이다.

알아야 할 것은 조건부확률의 평균과 공분산 값이다. 이 것을 알기 위해서 굳이 \(b\)와 \(\tau\)값을 계산할 필요는 없다.

---

가우시안 분포의 지수부는 다음과 같이 전개된다는 것이 중요한 포인트이다.

\[\begin{align} -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) &= -\frac{1}{2}(\boldsymbol{x}^{T}-\boldsymbol{\mu}^{T})\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\\ &= -\frac{1}{2}(\boldsymbol{x}^{T}\Sigma^{-1}-\boldsymbol{\mu}^{T}\Sigma^{-1})(\boldsymbol{x}-\boldsymbol{\mu})\\ &= -\frac{1}{2}(\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{x}-\boldsymbol{\mu}^{T}\Sigma^{-1}\boldsymbol{x}-\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{\mu}+\boldsymbol{\mu}^{T}\Sigma^{-1}\boldsymbol{\mu})\\ &= -\frac{1}{2}\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{x}+\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{\mu} + \text{const} \end{align}\]

여기서 상수부 \(\text{const}\)는 \(\boldsymbol{x}\)와 독립된 항들을 모은 것이다. 따라서 어떤 복잡한 함수라도 지수부를 정리했을 때 \(-\frac{1}{2}\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{x}+\boldsymbol{x}^{T}\Sigma^{-1}\boldsymbol{\mu} + \text{const}\)의 형태가 된다면 이 함수는 공분산 행렬 \(\Sigma\)와 평균벡터 \(\boldsymbol{\mu}\)를 가지는 가우시안 분포임을 알 수 있다. \(\boldsymbol{x}\)에 관한 이차항과 일차항의 계수를 살피면 된다는 것이다.

\(-\frac{1}{2}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})^{T}\Lambda_{aa}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})-\frac{1}{2}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})^{T}\Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})-\frac{1}{2}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})^{T}\Lambda_{ba}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})-\frac{1}{2}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})^{T}\Lambda_{bb}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\)에서 \(\boldsymbol{x}_{a}\)의 이차항은

\[-\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{aa}\boldsymbol{x}_{a}\]

이다. 따라서 공분산은

\[\sum_{a\vert b} = \Lambda_{aa}^{-1}\]

이다. 이제 평균벡터를 구하기 위해서는 \(\boldsymbol{x}_{a}\)의 일차항을 정리하면 된다. \(\boldsymbol{x}_{a}\)의 일차항은

\(-\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{aa}(-\boldsymbol{u}_{a})+\frac{1}{2}\boldsymbol{u}_{a}^{T}\Lambda_{aa}(-\boldsymbol{x}_{a}) \rightarrow \boldsymbol{x}_{a}^{T}\Lambda_{aa}\boldsymbol{u}_{a}\) 뒤의 항에 Transpose를 시키면 앞뒤가 같은 항이 된다.

\(-\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{u}_{b}) - \frac{1}{2}(\boldsymbol{x}_{b}-\boldsymbol{u}_{b})^{T}\Lambda_{ba}\boldsymbol{x}_{a} \rightarrow -\boldsymbol{x}_{a}^{T}\Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{u}_{b})\) 역시 마찬가지로 transpose

위의 결과 2개를 더한 값이 바로 \(\boldsymbol{x}_{a}\)의 일차항이 된다.

\[\boldsymbol{x}_{a}^{T}\{ \Lambda_{aa}\boldsymbol{\mu}_{a} - \Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\}\]

\(\boldsymbol{x}_{a}\)의 일차항의 계수는 \(\Sigma_{a\vert b}^{-1}\boldsymbol{\mu}_{a\vert b}\) 이어야 하므로

일차항의 계수는 공분산의 역행렬에 \(\boldsymbol{\mu}\)가 되어야 하기 때문에, 일차항의 계수 \(\{ \Lambda_{aa}\boldsymbol{\mu}_{a} - \Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\}\)에다가 \(\Sigma_{a\vert b}\)행렬을 곱해주면 된다. 이 때 \(\Sigma_{a\vert b} = \Lambda_{aa}^{-1}\)이기 때문에 \(\Lambda_{aa}^{-1}\)을 곱해준다.

\[\begin{align} \boldsymbol{\mu}_{a\vert b} &= \Sigma_{a\vert b} \{ \Lambda_{aa}\boldsymbol{\mu}_{a} - \Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\}\\ &= \boldsymbol{\mu}_{a} - \Lambda_{aa}^{-1}\Lambda_{ab}(\boldsymbol{x}_{b} - \boldsymbol{\mu}_{b}) \end{align}\]

주변 가우시안 분포 (Marginal Gaussian Distribution)

다음과 같은 주변분포를 계산하고자 한다.

\[p(\boldsymbol{x}_{a}) = \int p(\boldsymbol{x}_{a}, \boldsymbol{x}_{b})d\boldsymbol{x}_{b}\]

전략은 다음과 같다.

\[\begin{align} p(\boldsymbol{x}_{a}) &= \int p(\boldsymbol{x}_{a}, \boldsymbol{x}_{b})d\boldsymbol{x}_{b} \\ &= \int\alpha\exp\left\{ -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \right\} d\boldsymbol{x}_{b} \\ &= \int\alpha\exp\{ f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})+g(\boldsymbol{x}_{a})+\text{const} \}d\boldsymbol{x}_{b} \\ &= \int\alpha\exp\{ f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})-\tau+\tau+g(\boldsymbol{x}_{a})+\text{const} \}d\boldsymbol{x}_{b}\\ &= \int\alpha\exp\{ f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})-\tau\}\exp\{\tau+g(\boldsymbol{x}_{a})+\text{const} \}d\boldsymbol{x}_{b} \\ &= \alpha\exp\{\tau+g(\boldsymbol{x}_{a})+\text{const} \}\int\exp\{f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})-\tau\}d\boldsymbol{x}_{b} \\ &= \alpha\beta\exp\{\tau+g(\boldsymbol{x}_{a})+\text{const} \} \end{align}\]

• 위에서 함수 \(f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})\)는 원래 지수부를 \(\boldsymbol{x}_{a},\boldsymbol{x}_{b}\)파티션을 통해 전개한 식 중에서 \(\boldsymbol{x}_{b}\)을 포함한 모든 항들을 모은 식이다. 그리고 \(g(\boldsymbol{x}_{a})\)는 \(f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})\)에 포함된 항들을 제외한 항들 중 \(\boldsymbol{x}_{a}\)를 포함한 모든 항들을 모은식이다. \(\text{const}\)는 나머지 항들을 모은 식이다.
• \(f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})-\tau\)는 \(\boldsymbol{x}_{b}\)을 위한 완전제곱식이다.
• \(\alpha\exp\{\tau+g(\boldsymbol{x}_{a})+\text{const}\}\)는 \(\boldsymbol{x}_{b}\)와 독립적이므로 적분식 밖으로 나갈 수 있다.
• \(\tau+g(\boldsymbol{x}_{a})\)를 \(\boldsymbol{x}_{a}\)의 완전제곱식으로 만들면 \(\boldsymbol{x}_{b}\)의 평균벡터와 공분산행렬을 구할 수 있다.

파티션을 위한 이차형식을 다시 살펴본다.

\[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\] \[= -\frac{1}{2}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})^{T}\Lambda_{aa}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})-\frac{1}{2}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})^{T}\Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\\\\ -\frac{1}{2}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})^{T}\Lambda_{ba}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})-\frac{1}{2}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})^{T}\Lambda_{bb}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\]

이 식을 전부 펼치면 총 16개의 항이 있게 된다. 이 중 \(\boldsymbol{x}_{b}\)를 포함한 항들의 개수는 7개, 나머지 중에서 \(\boldsymbol{x}_{ㅁ}\)를 가진 항의 개수는 5개이다.

\[\begin{align}f(\boldsymbol{x}_{b},\boldsymbol{x}_{a}) &= -\frac{1}{2}\boldsymbol{x}_{b}^{T}\Lambda_{bb}\boldsymbol{x}_{b}+\frac{1}{2}\boldsymbol{x}_{b}^{T}\Lambda_{bb}\boldsymbol{\mu}_{b}+\frac{1}{2}\boldsymbol{\mu}_{b}^{T}\Lambda_{bb}\boldsymbol{x}_{b}-\frac{1}{2}\boldsymbol{x}_{b}^{T}\Lambda_{ba}\boldsymbol{x}_{a}+\frac{1}{2}\boldsymbol{x}_{b}^{T}\Lambda_{ba}\boldsymbol{\mu}_{a}-\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{ab}\boldsymbol{x}_{b}+\frac{1}{2}\boldsymbol{\mu}_{a}^{T}\Lambda_{ab}\boldsymbol{x}_{b} \\ &= -\frac{1}{2}\boldsymbol{x}_{b}^{T}\Lambda_{bb}\boldsymbol{x}_{b} + \boldsymbol{x}_{b}^{T}\{ \Lambda_{bb}\boldsymbol{\mu}_{b} - \Lambda_{ba}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})\} \end{align}\] \[\begin{align}g(\boldsymbol{x}_{a}) &= \frac{1}{2}\boldsymbol{\mu}_{b}^{T}\Lambda_{ba}\boldsymbol{x}_{a}+\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{ab}\boldsymbol{\mu}_{b}-\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{aa}\boldsymbol{x}_{a}+\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{aa}\boldsymbol{\mu}_{a}+\frac{1}{2}\boldsymbol{\mu}_{a}^{T}\Lambda_{aa}\boldsymbol{x}_{a} \\ &= -\frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{aa}\boldsymbol{x}_{a} + \boldsymbol{x}_{a}^{T} (\Lambda_{aa}\boldsymbol{\mu}_{a}+\Lambda_{ab}\boldsymbol{\mu}_{b})\end{align}\]

아래와 같이 \(f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})\)를 완전제곱식으로 만든다.

\[-\frac{1}{2}\boldsymbol{x}_{b}^{T}\Lambda_{bb}\boldsymbol{x}_{b}+\boldsymbol{x}_{b}^{T}\boldsymbol{m} = -\frac{1}{2}(\boldsymbol{x}_{b}-\Lambda_{bb}^{-1}\boldsymbol{m})^{T}\Lambda_{bb}(\boldsymbol{x}_{b}-\Lambda_{bb}^{-1}\boldsymbol{m})+\frac{1}{2}\boldsymbol{m}^{T}\Lambda_{bb}^{-1}\boldsymbol{m}\]

where \(\boldsymbol{m} = \Lambda_{bb}\boldsymbol{\mu}_{b} - \Lambda_{ba}(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a})\)

따라서 \(\tau = \frac{1}{2}\boldsymbol{m}^{T}\Lambda_{bb}^{-1}\boldsymbol{m}\)이고

\[\int\exp\{f(\boldsymbol{x}_{b},\boldsymbol{x}_{a})-\tau\}d\boldsymbol{x}_{b} = \int\exp\left\{ -\frac{1}{2}(\boldsymbol{x}_{b}-\Lambda_{bb}^{-1}\boldsymbol{m})^{T}\Lambda_{bb}(\boldsymbol{x}_{b}-\Lambda_{bb}^{-1}\boldsymbol{m}) \right\}d\boldsymbol{x}_{b}\]

이 값은 공분산 \(\Lambda_{bb}\)에만 종속되고 \(\boldsymbol{x}_{a}\)에 독립적이므로 \(\alpha\beta\exp\{\tau+g(\boldsymbol{x}_{a})+\text{const}\}\)의 지수부에만 집중하면 된다.

마지막으로 \(\tau+g(\boldsymbol{x}_{a})+\text{const}\)를 살펴보자.

\[\begin{align}\tau+g(\boldsymbol{x}_{a})+\text{const} &= \frac{1}{2}\boldsymbol{m}^{T}\Lambda_{bb}^{-1}\boldsymbol{m} - \frac{1}{2}\boldsymbol{x}_{a}^{T}\Lambda_{aa}\boldsymbol{x}_{a} + \boldsymbol{x}_{a}^{T}(\Lambda_{aa}\boldsymbol{\mu}_{a} + \Lambda_{ab}\boldsymbol{\mu}_{b})+\text{const} \\ &= -\frac{1}{2}\boldsymbol{x}_{a}^{T}(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})\boldsymbol{x}_{a} + \boldsymbol{x}_{a}^{T}(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})\boldsymbol{\mu}_{a}+\text{const} \end{align}\]

따라서 공분산은

\[\Sigma_{a} = (\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})^{-1}\]

이고, 평균 벡터는

\[\Sigma_{a}(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})\boldsymbol{\mu}_{a} = \boldsymbol{\mu}_{a}\]

공분산의 형태가 복잡하게 보이지만 Schur complement를 사용하면

\[(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})^{-1} = \Sigma_{aa}\]

임을 알 수 있다. 정리하자면

- \(\mathbb{E}[\boldsymbol{x}_{a}] = \boldsymbol{\mu}_{a}\)

- \(cov[\boldsymbol{x}_{a}] = \Sigma_{aa}\)

가우시안 분포를 위한 베이즈 정리 (Bayes’ Theorem for Gaussian Variables)

\(p(\boldsymbol{x})\)와 \(p(\boldsymbol{y}\vert \boldsymbol{x})\)가 주어져 있고 \(p(\boldsymbol{y}\vert \boldsymbol{x})\)의 평균은 \(\boldsymbol{x}\)의 선형함수이고 공분산은 \(\boldsymbol{x}\)와 독립적이라고 하자. 이제 \(p(\boldsymbol{x})\)와 \(p(\boldsymbol{y}\vert \boldsymbol{x})\)를 구할 것이다. 이 결과는 다음 시간에 배울 선형회귀(베이지안) 주요 내용을 유도하는 데 유용하게 쓰일 것이다.

\(p(\boldsymbol{x})\)와 \(p(\boldsymbol{y}\vert \boldsymbol{x})\)가 다음과 같이 주어진다고 하자.

\(p(\boldsymbol{x}) = \mathcal{N}(\boldsymbol{x}\vert \boldsymbol{\mu}, \Lambda^{-1})\)
\(p(\boldsymbol{y}\vert \boldsymbol{x}) = \mathcal{N}(\boldsymbol{y}\vert \boldsymbol{Ax+b}, \boldsymbol{L}^{-1})\)

\(p(\boldsymbol{x}\vert \boldsymbol{x})\)의 평균이 \(\boldsymbol{x}\) 에 관한 선형함수임을 기억하자.

먼저 \(\boldsymbol{z} = \begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix}\)를 위한 결합확률분포를 구하자. 이 결합확률분포를 구하고 나면 \(p(\boldsymbol{y}\)와 \(p(\boldsymbol{x}\vert \boldsymbol{y})\)는 앞에서 얻은 결과에 의해 쉽게 유도할 수 있다. 먼저 로그값을 생각해보자.

\[\begin{align}\ln p(\boldsymbol{z}) &= \ln p(\boldsymbol{x}) + \ln p(\boldsymbol{y}\vert \boldsymbol{x}) \\ &= -\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T}\Lambda(\boldsymbol{x}-\boldsymbol{\mu}) -\frac{1}{2}(\boldsymbol{y}-\boldsymbol{Ax}-\boldsymbol{b})^{T}\boldsymbol{L}(\boldsymbol{y}-\boldsymbol{Ax}-\boldsymbol{b})+\text{const} \end{align}\]

\(\boldsymbol{z}\)의 이차항은 다음과 같다.

위의 식에서 x와 y에 관한 항들을 모은 식이 아래와 같다.
아래의 식을 확인하기 전에 \(\begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix}^{T}\begin{bmatrix} A & B \cr C & D \end{bmatrix}\begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix}\)의 결과가 어떻게 나오는 지 확인하자.
\(\begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix}^{T}\begin{bmatrix} A & B \cr C & D \end{bmatrix}\begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix} = \boldsymbol{x}^{T}A\boldsymbol{x} + \boldsymbol{y}^{T}C\boldsymbol{x} + \boldsymbol{x}^{T}B\boldsymbol{y} + \boldsymbol{y}^{T}D\boldsymbol{y}\)이 된다. 이 \(\boldsymbol{x}\), \(\boldsymbol{y}\) 사이에 있는 식을 찾아서 행렬을 만들면 아래의 행렬이 됨을 알 수 있다.

\[-\frac{1}{2}\boldsymbol{x}^{T}(\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA})\boldsymbol{x} - \frac{1}{2}\boldsymbol{y}^{T}\boldsymbol{Ly} + \frac{1}{2}\boldsymbol{y}^{T}\boldsymbol{LAx} + \frac{1}{2}\boldsymbol{x}^{T}\boldsymbol{A}^{T}\boldsymbol{Ly}\]

\(= -\frac{1}{2}\begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix}^{T}\begin{bmatrix} \Lambda + \boldsymbol{A}^{T}\boldsymbol{LA} & -\boldsymbol{A}^{T}\boldsymbol{L} \cr -\boldsymbol{LA} & \boldsymbol{L} \end{bmatrix}\begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix}\)
\(= -\frac{1}{2}\boldsymbol{z}^{T}\boldsymbol{Rz}\)

\[\boldsymbol{R} = \begin{bmatrix} \Lambda + \boldsymbol{A}^{T}\boldsymbol{LA} & -\boldsymbol{A}^{T}\boldsymbol{L} \cr -\boldsymbol{LA} & \boldsymbol{L} \end{bmatrix}\]

따라서 공분산은

\[cov[\boldsymbol{z}] = \boldsymbol{R}^{-1} = \begin{bmatrix} \Lambda^{-1} & \Lambda^{-1}\boldsymbol{A}^{T} \cr \boldsymbol{A}\Lambda^{-1} & \boldsymbol{L}^{-1}+\boldsymbol{A}\Lambda^{-1}\boldsymbol{A}^{T} \end{bmatrix}\]

이다.

평균벡터를 찾기 위해서 \(\boldsymbol{z}\)의 1차항을 정리한다.

\[\boldsymbol{x}^{T}\Lambda\boldsymbol{\mu} - \boldsymbol{x}^{T}\boldsymbol{A}^{T}\boldsymbol{Lb} + \boldsymbol{y}^{T}\boldsymbol{Lb} = \begin{bmatrix} \boldsymbol{x} \cr \boldsymbol{y} \end{bmatrix}^{T}\begin{bmatrix} \Lambda\boldsymbol{\mu}-\boldsymbol{A}^{T}\boldsymbol{Lb} \cr \boldsymbol{Lb} \end{bmatrix}\]

따라서 평균벡터는

\[\mathbb{E}[\boldsymbol{z}] = \boldsymbol{R}^{-1}\begin{bmatrix} \Lambda\boldsymbol{\mu}-\boldsymbol{A}^{T}\boldsymbol{Lb} \cr \boldsymbol{Lb} \end{bmatrix} = \begin{bmatrix} \boldsymbol{\mu} \cr \boldsymbol{A\mu}+\boldsymbol{b} \end{bmatrix}\]

\(\boldsymbol{y}\)를 위한 주변확률분포의 평균과 공분산은 앞의 “주변 가우시안 분포” 결과를 적용하면 쉽게 구할 수 있다.

공분산(\(cov[\boldsymbol{y}]\))의 경우는 앞에서 \(cov[\boldsymbol{z}] = \boldsymbol{R}^{-1} = \begin{bmatrix} \Lambda^{-1} & \Lambda^{-1}\boldsymbol{A}^{T} \cr \boldsymbol{A}\Lambda^{-1} & \boldsymbol{L}^{-1}+\boldsymbol{A}\Lambda^{-1}\boldsymbol{A}^{T} \end{bmatrix}\)식의 (2,2) 원소이기 때문에 \(\boldsymbol{L}^{-1} + \boldsymbol{A}\Lambda^{-1}\boldsymbol{A}^{T}\)가 된다.

\(\mathbb{E}[\boldsymbol{y}] = \boldsymbol{A\mu} + \boldsymbol{b}\)
\(cov[\boldsymbol{y}] = \boldsymbol{L}^{-1} + \boldsymbol{A}\Lambda^{-1}\boldsymbol{A}^{T}\)

마찬가지로 조건부 확률 \(p(\boldsymbol{x}\vert \boldsymbol{y})\)의 평균과 공분산은 “조건부 가우시안 분포” 결과를 적용해 유도할 수 있다.

\(\mathbb{E}[\boldsymbol{x}\vert \boldsymbol{y}] = (\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA})^{-1}\{ \boldsymbol{A}^{T}\boldsymbol{L}(\boldsymbol{y} - \boldsymbol{b}) + \Lambda\boldsymbol{\mu} \}\)
\(cov[\boldsymbol{x}\vert \boldsymbol{y}] = (\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA})^{-1}\)

조건부 확률의 공분산: \(\Sigma_{a\vert b} = \Lambda_{aa}^{-1}\), 평균 벡터: \(\boldsymbol{\mu}_{a\vert b} = \Sigma_{a\vert b}\{ \Lambda_{aa}\boldsymbol{\mu}_{a} - \Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\}\)

\(\boldsymbol{R} = \begin{bmatrix} \Lambda + \boldsymbol{A}^{T}\boldsymbol{LA} & -\boldsymbol{A}^{T}\boldsymbol{L} \cr -\boldsymbol{LA} & \boldsymbol{L} \end{bmatrix}\) 공분산을 먼저보면, 공분산은 \(\Lambda_{aa}^{-1}\)이라고 했는데, 이것은 \(R\)에서 이미 구했다. \(\boldsymbol{R}\)이 바로 \(\Lambda\)이기 때문에, \(R\)에서 \(aa\)에 해당하는 부분은 \(\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA}\)이기 때문에 이것의 역행렬(\((\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA})^{T}\))이 된다.

평균 벡터(\(\boldsymbol{\mu}_{a\vert b} = \Sigma_{a\vert b}\{ \Lambda_{aa}\boldsymbol{\mu}_{a} - \Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\}\))의 경우, 공분산 행렬은 앞에서 구했기 때문에 곱하고, ‘{}’ 안의 수식만 해결하면 된다. \(\Lambda_{aa} = (\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA})\), \(\boldsymbol{\mu}_{a}\)는 \(\boldsymbol{x}\)를 의미하고 있기 때문에 \(\mathbb{E}[\boldsymbol{z}] = \begin{bmatrix} \boldsymbol{\mu} \cr \boldsymbol{A\mu}+\boldsymbol{b} \end{bmatrix}\)식에서 \(\boldsymbol{\mu}\)를 의미한다. \(\Lambda_{ab}\)는 \(\boldsymbol{R}\)에서 \(-\boldsymbol{A}^{T}\boldsymbol{L}\)이고, \(\boldsymbol{x}_{b}\)는 \(\boldsymbol{y}\)이고, \(\boldsymbol{\mu}_{b}\)는 \(\mathbb{E}[\boldsymbol{z}] = \begin{bmatrix} \boldsymbol{\mu} \cr \boldsymbol{A\mu}+\boldsymbol{b} \end{bmatrix}\)에서 아랫부분 이기 때문에 \(\boldsymbol{A\mu}+\boldsymbol{b}\)가 된다.

정리하자면, \(\boldsymbol{\mu}_{a\vert b} = \Sigma_{a\vert b}\{ \Lambda_{aa}\boldsymbol{\mu}_{a} - \Lambda_{ab}(\boldsymbol{x}_{b}-\boldsymbol{\mu}_{b})\} = (\Lambda + \boldsymbol{A}^{T}\boldsymbol{LA})^{T}\boldsymbol{\mu} - (-\boldsymbol{A}^{T}\boldsymbol{L})(\boldsymbol{y}-(\boldsymbol{A\mu}+\boldsymbol{b}))\) 이렇게 된다.
다시 정리하면, \(\Lambda\boldsymbol{\mu} + \boldsymbol{A}^{T}\boldsymbol{LA}\boldsymbol{\mu} + \boldsymbol{A}^{T}\boldsymbol{L}\boldsymbol{y}-\boldsymbol{A}^{T}\boldsymbol{L}\boldsymbol{A\mu}-\boldsymbol{A}^{T}\boldsymbol{L}\boldsymbol{b}\) 이렇게 되고 \(\boldsymbol{A}^{T}\boldsymbol{LA}\boldsymbol{\mu}\)가 서로 상쇄되고, 나머지는 \(\Lambda\boldsymbol{\mu} + \boldsymbol{A}^{T}\boldsymbol{L}\boldsymbol{y} -\boldsymbol{A}^{T}\boldsymbol{L}\boldsymbol{b}\) 이렇게 되고 다시 \(\Lambda\boldsymbol{\mu} + \boldsymbol{A}^{T}\boldsymbol{L}(\boldsymbol{y} -\boldsymbol{b})\) 이렇게 된다.
이것이 평균 벡터의 {}안을 채우게 되면 위의 식이 나오는 것이다.

여태까지 한 것은 \(\boldsymbol{z}\)에 대한 공분산과 평균 벡터를 구한다음에 조건부 확률에 적용한 것이다.

가우시안 분포의 최대우도 (Maximum Likelihood for the Gaussian)

Why log-likelihood instead of likelihood?
Easier to deal with differentiation, integration, and exponential families. product를 log로 바꿔주면 summation이 되는데 이는 계산량 감소의 이점이 있다. For practical purposes it is more convenient to work with the log-likelihood function in maximum likelihood estimation (wikipedia). In addition to the mathematical convenience from this, the adding process of log-likelihood has an intuitive interpretation, as often expressed as “support” from the data. When the parameters are estimated using the log-likelihood for the maximum likelihood estimation, each data point is used by being added to the total log-likelihood. As the data can be viewed as an evidence that support the estimated parameters, this process can be interpreted as “support from independent evidence adds”, and the log-likelihood is the “weight of evidence”. Interpreting negative log-probability as information content or surprisal, the support (log-likelihood) of a model, given an event, is the negative of the surprisal of the event, given the model: a model is supported by an event to the extent that the event is unsurprising, given the model (wikipedia).

\(\boldsymbol{X}\): 대문자로 표시되어 있을 경우, 데이터가 여러개인 경우를 의미.

가우시안 분포에 의해 생성된 데이터 \(\boldsymbol{X} = (\boldsymbol{x}_{1},\cdots,\boldsymbol{x}_{n})^{T}\)가 주어졌을 때, 우도를 최대화하는 파리미터 값들(평균, 공분산)을 찾는 것이 목표라고 하자. 로그우도 함수는 다음과 같다.

\[\ln p(\boldsymbol{X}\vert \boldsymbol{\mu}, \Sigma) = -\frac{ND}{2}\ln(2\pi) -\frac{N}{2}\ln\vert \Sigma\vert - \frac{1}{2}\sum_{n=1}^{N}(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\boldsymbol{x}_{n}-\boldsymbol{\mu})\]

ML - 평균 벡터

먼저 우도를 최대화하는 평균벡터 \(\boldsymbol{\mu}_{ML}\)을 찾아보자.

\(\boldsymbol{y} = (\boldsymbol{x}-\boldsymbol{\mu})\)라 하면 다음의 식이 유도된다.

이차형식을 \(\boldsymbol{\mu}\) 에 대해서 미분한 결과는 아래와 같다.

행렬미분에서 배운 이차형식에서 미분을 하는 과정이 있었다.
\(\Delta_{x}x^{T}Ax = 2Ax\) 라는 공식을 \(\frac{\partial}{\partial\boldsymbol{y}}\boldsymbol{y}^{T}\Sigma^{-1}\boldsymbol{y}\frac{\partial\boldsymbol{y}}{\partial\boldsymbol{\mu}}\) 이 식에 활용하면, 아래와 같은 결과를 얻을 수 있다.
\(\boldsymbol{y}\)를 \(\boldsymbol{\mu}\)에 대해 미분한 값이 앞에서 \(-\)가 있기 때문에 결과적으로 \(-2Ax\)가 된 것이다.
\(\Sigma^{-1}\)이 정확도 행렬이기 때문에 \(\Lambda\)로 바꿔주었다.
https://marquis08.github.io/devcourse2/linearalgebra/mathjax/ML-basics-Linear-Algebra/#%ED%96%89%EB%A0%AC%EB%AF%B8%EB%B6%84-matrix-calculus

\[\frac{\partial}{\partial\boldsymbol{\mu}}(\boldsymbol{x}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) = \frac{\partial}{\partial\boldsymbol{y}}\boldsymbol{y}^{T}\Sigma^{-1}\boldsymbol{y}\frac{\partial\boldsymbol{y}}{\partial\boldsymbol{\mu}} = -2\Sigma^{-1}\boldsymbol{y} \equiv -2\Lambda\boldsymbol{y}\]

여기까지는 \(- \frac{1}{2}\sum_{n=1}^{N}\) 안에 있는 이차형식(\((\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\boldsymbol{x}_{n}-\boldsymbol{\mu})\))을 미분한 결과를 도출해 낸 것임.

따라서,

\[\frac{\partial}{\partial\boldsymbol{\mu}}\ln p(\boldsymbol{X}\vert \boldsymbol{\mu}, \Sigma) = -\frac{1}{2}\sum_{i=1}^{N}-2\Lambda(\boldsymbol{x}_{i}-\boldsymbol{\mu}) = \Lambda\sum_{i=1}^{N}(\boldsymbol{x}_{i}-\boldsymbol{\mu}) = 0\]

\(\Lambda\sum_{i=1}^{N}(\boldsymbol{x}_{i}-\boldsymbol{\mu})\): 각각의 \(\boldsymbol{x}_{i}\)에 대해서 \(\boldsymbol{\mu}\)를 빼준 것을 다 더하고 \(\Lambda\)를 곱해준 것.
최대우도해를 구하기 위해서 이 값을 0으로 놓고 풀었을 때 그 결과는 아래와 같다.

\[\boldsymbol{\mu}_{ML} = \frac{1}{N}\sum_{i=1}^{N}\boldsymbol{x}_{i} = \boldsymbol{\bar x}\]

관찰한 각 데이터를 더한 것을 N으로 나눈 것이 된다. 이는 관찰한 데이터의 평균값으로 볼 수 있다. 이것의 \(\boldsymbol{\mu}\)의 ML이 되는 것임.

ML - 공분산

정확도 행렬 \(\Lambda\)에 대한 함수로 놓고 풀면 식이 간단해 진다.

다음으로 우도를 최대화하는 공분산행렬 \(\Sigma_{ML}\)을 찾아보자.

아래의 식에서 \(l\)은 정확도 행렬과 관련있는 부분(종속적인)만 남겨논 것이다. (상수는 최대화와 상관이 없기 때문에)

trace가 나오는데, 원래 \(-\frac{1}{2}\sum_{i=1}^{N}-2\Lambda(\boldsymbol{x}_{i}-\boldsymbol{\mu})\) 이 값은 scalar 값인데, scalar 값을 원소가 1개인 행렬로 생각할 수 있다. 이 때 이 행렬의 trace 값은 그 행렬 자체라는 성질을 활용함. 아래의 선형대수 결과 리스트의 2번째 성질을 보면 trace를 씌워도 같은 값임을 알 수 있다. 또한 trace를 씌우면 뒤에 있던 \(\boldsymbol{x}\)가 앞으로 이동한 것을 알 수 있는데, trace가 여러개의 행렬의 곱일때 순서를 cycle해도 동일한 값이기 때문에 가능하다.
이 성질을 사용해서 \(tr((\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\Lambda)\) 아래의 이 식에서 \((\boldsymbol{x}_{n}-\boldsymbol{\mu})\)가 앞으로 나오게 된 것임.
\(\boldsymbol{S}\)를 보면 trace 밖에 있던 summation이 trace안으로 들어온 것을 알 수 있는데, 이것도 역시 아래의 선형대수 성질 중에서 3번째 성질인 \(tr(A)+tr(A)=tr(A+B)\) 이것을 활용한 것임.

\[l(\Lambda) = \frac{N}{2}\ln\vert \Lambda\vert - \frac{1}{2}\sum_{n=1}^{N}tr((\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\Lambda) = \frac{N}{2}\ln\vert \Lambda\vert - \frac{1}{2}tr(\boldsymbol{S}\Lambda)\] \[\boldsymbol{S} = \sum_{i=1}^{N}(\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\]

\(\Lambda\) 에 대해 결과적으로 나온 식이 \(\frac{N}{2}\ln\vert \Lambda\vert - \frac{1}{2}tr(\boldsymbol{S}\Lambda)\) 이고, 이 식을 \(\Lambda\)에 관해서 미분을 하면 되는 것이다.
\(\Lambda\)는 벡터가 아니고 행렬이기 때문에 행렬미분 성질을 활용하면 쉽게 풀 수 있음.
\(\Lambda\)의 판별식의 로그값을 \(\Lambda\)에 대해서 미분을 하는데, 이 것은 아래의 선형대수 성질 중에서 \(\frac{\partial}{\partial\boldsymbol{A}}\ln\vert \boldsymbol{A}\vert = (\boldsymbol{A}^{-1})^{T}\)을 활용 함. 따라서 \(\ln\vert \Lambda\vert = (\Lambda^{-1})^{T}\)가 된다.
\(tr(\boldsymbol{S}\Lambda)\)는 \(\frac{\partial}{\partial\boldsymbol{A}}tr(\boldsymbol{BA}) = \boldsymbol{B}^{T}\) 이 성질을 활용함. 따라서 \(tr(\boldsymbol{S}\Lambda) = \boldsymbol{S}^{T}\)가 되는 것임.

\[\frac{\partial l(\Lambda)}{\partial \Lambda} = \frac{N}{2}(\Lambda^{-1})^{T}-\frac{1}{2}\boldsymbol{S}^{T} = 0\]

위의 결과로 나온 \(\frac{N}{2}(\Lambda^{-1})^{T}-\frac{1}{2}\boldsymbol{S}^{T}\)을 0으로 놓고 \(\Lambda\)에 관해서 풀면 된다.
결과적으로 \((\Lambda_{ML}^{-1}) = \frac{1}{N}\boldsymbol{S}\) 이 식이 나오는데 이 때, \(\Lambda\)은 정확도 행렬인데, 이 것의 역행렬이 \(\Sigma\) 이기 때문에 이것이 우리가 찾고자 했던 공분산 행렬이다.

\[(\Lambda_{ML}^{-1}) = \Sigma_{ML} = \frac{1}{N}\boldsymbol{S}\] \[\Sigma_{ML} = \frac{1}{N}\sum_{i=1}^{N}(\boldsymbol{x}_{n}-\boldsymbol{\mu})(\boldsymbol{x}_{n}-\boldsymbol{\mu})^{T}\]

\(\boldsymbol{S}\)를 대입해주면 \(\Sigma_{ML}\) 이 된다.

위의 식 유도를 위해 아래의 기본적인 선형대수 결과를 사용하였다.

• \(\vert \boldsymbol{A}^{-1}\vert = l/\vert \boldsymbol{A}\vert\)
• \(\boldsymbol{x}^{T}\boldsymbol{Ax} = tr(\boldsymbol{x}^{T}\boldsymbol{Ax}) = tr(\boldsymbol{xx}^{T}\boldsymbol{A}) \)
• \(tr(\boldsymbol{A}) + tr(\boldsymbol{B}) = tr(\boldsymbol{A}+\boldsymbol{B}) \)
• \(\frac{\partial}{\partial\boldsymbol{A}}tr(\boldsymbol{BA}) = \boldsymbol{B}^{T} \)
• \(\frac{\partial}{\partial\boldsymbol{A}}\ln\vert \boldsymbol{A}\vert = (\boldsymbol{A}^{-1})^{T}\)

여기서 한가지 짚고 넘어가야할 부분은, 식을 간단하게 하기 위해 \(\Lambda\)라는 정확도 행렬을 사용해서 공분산 행렬을 유도했는데, \(\Lambda\)에 관해서 푼 최적해를 단순히 역행렬을 시켜주는 것이 원래 찾고자 했던 \(\Sigma\)의 최대값이 맞는가를 생각해볼 필요가 있다.

정확도 행렬의 역행렬의 최적해가 공분산 행렬의 최대값과 일치할까?

\((\Lambda_{ML})^{-1} = \Sigma_{ML}\)이해하기

일반적으로 다음이 성립한다. 함수 \(h(\boldsymbol{X}) = \boldsymbol{Y}\)가 일대일이고 다음과 같은 최소값들이 존재한다고 하자.

일대일 이기 때문에 역함수(\(h^{-1}\))도 존재한다.
f와 h가 composite function(합성함수)로 주어져있다.

\[\boldsymbol{X}^{*} = \arg\min_{X}f(h(\boldsymbol{X}))\] \[\boldsymbol{Y}^{*} = \arg\min_{Y}f(\boldsymbol{Y})\]

\(\boldsymbol{Y}^{*}\)라는 값을 구했다고 가정하고, \(\boldsymbol{X}\) 대신에 \(\boldsymbol{Y}^{*}\)를 대입하면, \(f(h(h^{-1}(\boldsymbol{Y}^{*})))\) 이 값이 된다. 이는 h가 항등함수(Identity Function)이 되기 때문에 \(f(\boldsymbol{Y}^{*})\) 이 값이 결과적으로 됨. 따라서 \(h^{-1}(\boldsymbol{Y}^{*})\)를 넣었을 때 최소값이 \(\boldsymbol{X}^{*}\)이 때문에 아래의 식이 성립함.

만약에 일대일이 아니라면 성립하지 않는다는 사실을 기억하자.

\(f(h(h^{-1}(\boldsymbol{Y}^{*}))) = f(\boldsymbol{Y}^{*})\)이므로 \(h^{-1}(\boldsymbol{Y}^{*}) = \boldsymbol{X}^{*}\)이 성립한다. 위의 경우에 적용하자면,

\(l\)이라는 \(\Lambda\)에 관한 함수를 최소화 시키는 \(\Lambda_{ML}\)을 구했는데, 위에서 \(\boldsymbol{Y}^{*}\)라고 생각하면 됨.
일대일이기 때문에 역함수연산이 가능하고 결국, \(h^{-1}\) 를 적용하게 되면, 결국 역행렬 연산이기 때문에, \((\Lambda_{ML})^{-1} = \Sigma_{ML}\) 가 되는 것임.

\[\Lambda_{ML} = \arg\min_{\Lambda}l(\Lambda)\]

역행렬 연산이 일대일함수\((h)\)를 정의하기 때문에, \(h^{-1}(\Lambda_{ML}) = \Sigma_{ML}\)이 되고, \((\Lambda_{ML})^{-1} = \Sigma_{ML}\)이 성립한다. ㅇ

가우시안 분포를 위한 베이지안 추론 (Bayesian Inference for the Gaussian)

MLE 방법은 파라미터들 (\(\boldsymbol{\mu}, \Sigma\))의 하나의 값만을 구하게 해준다. 베이지안 방법을 사용하면 파라미터의 확률분포 자체를 구할 수 있게 된다.
단변량 가우시안 확률변수 \(x\)의 \(\mu\)를 베이지안 추론을 통해 구해보자(분산 \(\sigma^2\)는 주어졌다고 가정). 목표는 \(\mu\)의 사후확률 \(p(\mu\vert \boldsymbol{X})\)을 우도함수 \(p(\boldsymbol{X}\vert \mu)\)와 사전확률 \(p(\boldsymbol{X}\vert \mu)\)을 통해 구하는 것이다.

• 우도함수

\[p(\boldsymbol{x}\vert \mu) = \prod_{n=1}^{N}p(\boldsymbol{x}_{n}\vert \mu) = \frac{1}{(2\pi\sigma^2)^{N/2}}\exp\left\{-\frac{1}{2\sigma^2}\sum_{n=1}^{N}(x_{n}-\mu)^2 \right\}\]

• 사전확률

\[p(\mu) = \mathcal{N}(\mu\vert \mu_{0}, \sigma_{0}^{2})\]

• 사후확률

\[\begin{align}p(\mu\vert x) &= \mathcal{N}(\mu\vert \mu_{N}, \sigma_{N}^{2}) \\\\ \mu_{N} &= \frac{\sigma^2}{N\sigma_{0}^2+\sigma^2}\mu_{0}+\frac{N\sigma_{0}^2}{N\sigma_{0}^2+\sigma^2}\mu_{ML} \\\\ \frac{1}{\sigma_{N}^{2}} &= \frac{1}{\sigma_{0}^{2}} + \frac{N}{\sigma^2} \\\\ \mu_{ML} &= \frac{1}{N}\sum_{n=1}^{N}x_{n} \end{align}\]

Appendix

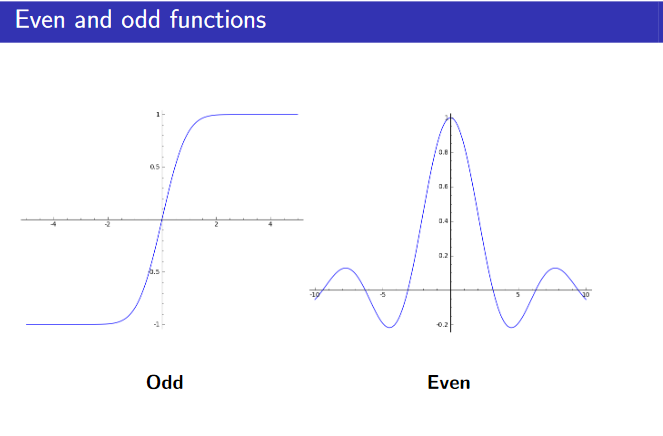
Odd & Even Function

\(f(x) = x^2\)
\(f(2) = f(-2)\)
\(f(x) = f(-x)\)

“Reflectional”, “EVEN”

\(f(x) = x^3\)
\(-f(2) = f(-2)\)
\(f(-x) = -f(x)\)

“Rotational”, “ODD”

Integration by Completing the square

정확도 행렬??

Minimal-mistakes

Video Embedding for youtube:

{% include video id=”XsxDH4HcOWA” provider=”youtube” %}

other video providers: https://mmistakes.github.io/minimal-mistakes/docs/helpers/

MathJax

escape unordered list
- \(cov[\boldsymbol{x}_{a}] = \Sigma_{aa}\):

\- $$cov[\boldsymbol{x}_{a}] = \Sigma_{aa}$$ 

\setminus
\(\{A\}\setminus\{B\}\):

$$\{A\}\setminus\{B\}$$

adjustable parenthesis
\(\left( content \right)\):

$$\left( content \right)$$

Matrix with parenthesis \(\begin{pmatrix}1 \cr 1 \end{pmatrix}\):

$$\begin{pmatrix}1 \cr 1 \end{pmatrix}$$

References

Pattern Recognition and Machine Learning: https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
Odd and Even functions: https://www.shsu.edu/~kws006/Precalculus/1.4_Function_Symmetries_files/1.4%20FunctionSymmetries%20slides%204to1.pdf
why log-likelihood: https://math.stackexchange.com/questions/892832/why-we-consider-log-likelihood-instead-of-likelihood-in-gaussian-distribution
why log-likelihood: https://www.quora.com/What-is-the-advantage-of-using-the-log-likelihood-function-versus-the-likelihood-function-for-maximum-likelihood-estimation
why log-likelihood: https://en.wikipedia.org/wiki/Likelihood_function#Log-likelihood