ML basics - Probability Distributions 1

밀도추정(Density Estimation)

\(N\)개의 관찰데이터(observations) \(\mathbf{x}_1,\ldots\mathbf{x}_N\)가 주어졌을 때 분포함수 \(p(\mathbf{x})\)를 찾는 것

• \(p(\mathbf{x})\)를 파라미터화된 분포로 가정한다. 회귀, 분류문제에서는 주로 \(p(t\vert \mathbf{x})\), \(p(\mathcal{C}\vert \mathbf{x})\)를 추정한다.

• 그 다음 분포의 파라미터를 찾는다. 빈도주의 방법(Frequentist’s way): 어떤 기준(예를 들어 likelihood)을 최적화시키는 과정을 통해 파라미터 값을 정한다. 파라미터의 하나의 값을 구하게 된다. 베이지언 방법(Bayesian way): 먼저 파라미터의 사전확률(prior distribution)을 가정하고 Bayes’ rule을 통해 파라미터의 사후확률(posterior distribution)을 구한다.

• 파라미터를 찾았다면(한 개의 값이든 분포든) 그것을 사용해 “예측”할 수 있다(\(t\)나 \(\mathcal{C}\)).

켤레사전분포(Conjugate Prior): 사후확률이 사전확률과 동일한 함수형태를 가지도록 해준다.

이항변수(Binary Variables): 빈도주의 방법

이항 확률변수(binary random variable) \(x\in \{0, 1\}\) (예를 들어 동전던지기)가 다음을 만족한다고 하자.

\[p(x=1 \vert \mu) = \mu, p(x=0 \vert \mu) = 1 - \mu\]

\(p(x)\)는 베르누이 분포(Bernoulli distribution)로 표현될 수 있다.

\[\mathrm{Bern}(x \vert \mu) = \mu^x (1-\mu)^{1-x}\]

기댓값, 분산

• \(\mathbb{E}[x] = \mu\)
• \(\mathrm{var}[x] = \mu(1-\mu)\)

우도함수 (Likelihood Function)

\(x\)값을 \(N\)번 관찰한 결과를 \(\mathcal{D} = \{x_1,\ldots,x_N\}\)라고 하자. 각 \(x\)가 독립적으로 \(p(x\vert \mu)\)에서 뽑혀진다고 가정하면 다음과 같이 우도함수(\(\mu\)의 함수인)를 만들 수 있다.

\[p(\mathcal{D}\vert \mu) = \prod_{n=1}^N p(x_n\vert \mu) = \prod_{n=1}^N \mu^{x_n} (1-\mu)^{1-x_n}\]

빈도주의 방법에서는 \(\mu\)값을 이 우도함수를 최대화시키는 값으로 구할 수 있다. 또는 아래와 같이 로그우도함수를 최대화시킬 수도 있다.

\[\ln p(\mathcal{D}\vert \mu) = \sum_{n=1}^N \ln p(x_n\vert \mu) = \sum_{n=1}^N \{x_n\ln \mu + (1-x_n)\ln(1-\mu)\}\]

로그로 바꿔줘서 곱 \(\prod\)의 형태에서 합 \(\sum\)의 형태로 변환시킨다는데 로그했을때 합으로 왜 되는지

\(\mu\)의 최대우도 추정치(maximum likelihood estimate)는

\[\mu^{\mathrm{ML}} = \frac{m}{N} ~~\mathrm{with}~~ m = (\#\mathrm{observations~of}~ x=1)\]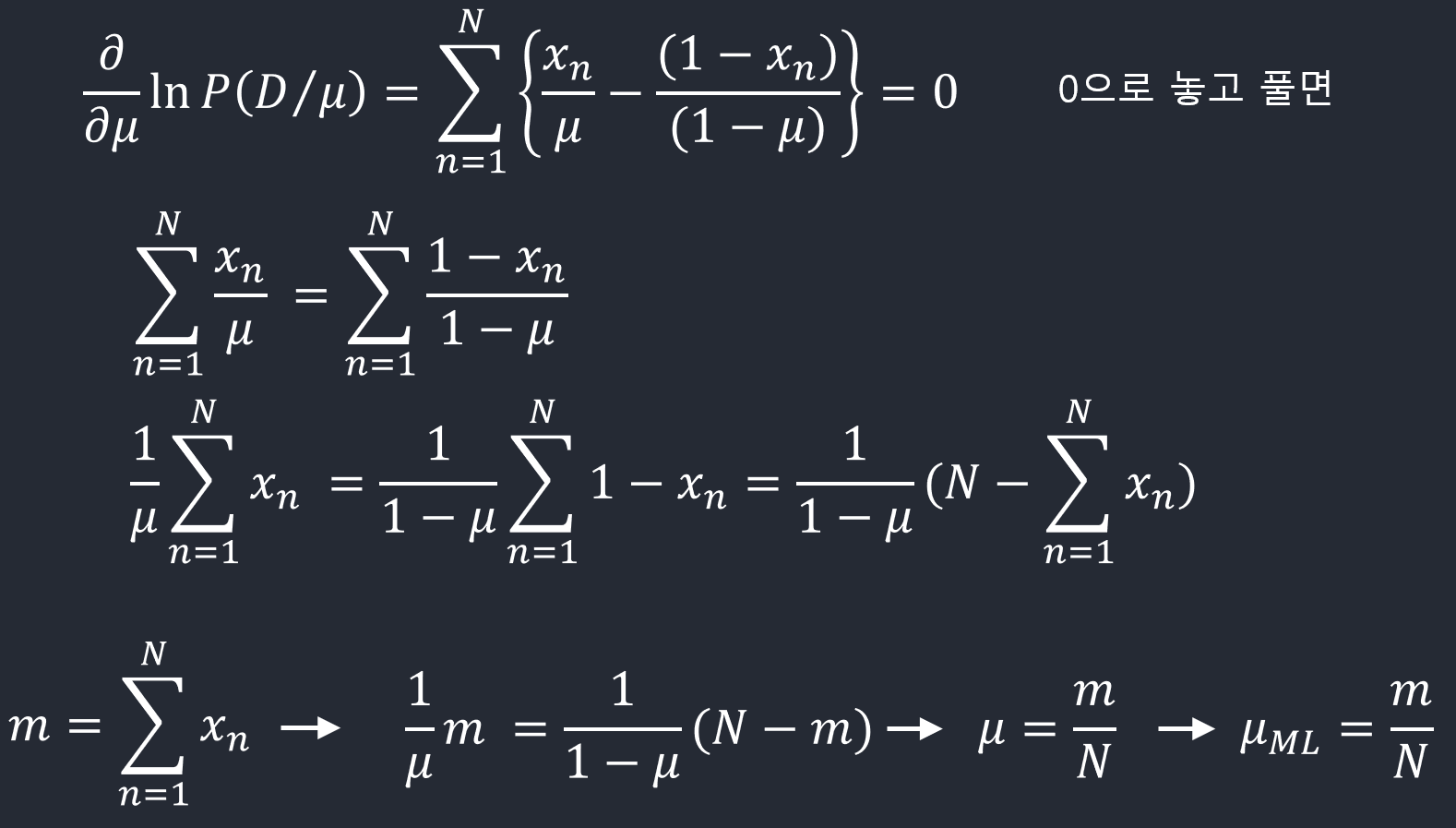

\(N\)이 작은 경우에 위 MLE는 과적합(overfitting)된 결과를 낳을 수 있다. \(N = m = 3 \to \mu^{\mathrm{ML}} = 1\)!

이항변수(Binary Variables): 베이지언 방법

이항분포 (Binomial Distribution)

\(\mathcal{D} = \{x_1,\ldots,x_N\}\)일 때, 이항변수 \(x\)가 1인 경우를 \(m\)번 관찰할 확률

\[\mathrm{Bin}(m\vert N,\mu) = {N \choose m}\mu^m(1-\mu)^{N-m}\] \[{N \choose m} = \frac{N!}{(N-m)!m!}\]

\(N\) = data size
\(\mu\) = parameter

• \(\mathbb{E}[m] = \sum_{m=0}^N m\mathrm{Bin}(m\vert N,\mu) = N\mu\)
• \(\mathrm{var}[m] = \sum_{m=0}^N (m-\mathbb{E}[m])^2\mathrm{Bin}(m\vert N,\mu) = N\mu(1-\mu)\)

데이터를 보는 관점

• 베르누이 시행의 반복: \(x_1,\ldots,x_N\) 각각이 확률변수
• \(x\)가 1인 경우를 몇 번 관찰했는가?: 하나의 확률변수 \(m\): binomial일 경우

베이지안 방법을 쓰기 위해서 데이터의 우도를 구해야 하는데 이항분포를 가정하면 우도함수가 하나의 변수 \(m\)으로(\(x_1,\ldots,x_N\) 대신) 표현가능하므로 간편해진다.

베타분포 (Beta Distribution)

베이지언 방법으로 문제를 해결하기 위해 베타분포를 켤레사전분포(conjugate prior)로 사용한다.

\[\mathrm{Beta}(\mu\vert a,b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1}\]

감마함수 \(\Gamma(x)\)는 다음과 같이 정의된다.

\(\Gamma(x) = \int_0^{\infty}u^{x-1}e^{-u}\mathrm{d}u\):
\(u^{x-1}e^{-u}\mathrm{d}u\) 을 u에 대해서 0~int까지 적분한다.

감마함수는 계승(factorial)을 실수로 확장시킨다. \(\Gamma(n) = (n-1)!\)

\(\Gamma(x) = (x-1)\Gamma(x-1)\)임을 증명하기

Using integration by parts \(\int_0^{\infty}a\mathrm{d}b = \left. ab\right\vert_0^{\infty} - \int_0^{\infty}b\mathrm{d}a\)

\[\begin{align*} a &= u^{x-1} &\ \mathrm{d}b &= -e^{-u}\mathrm{d}u\\ b &= e^{-u} &\ \mathrm{d}a &= (x-1)u^{x-2}\mathrm{d}u\\ \Gamma(x) &= \left. u^{x-1}(-e^{-u})\right\vert_0^{\infty} + \int_0^{\infty} (x-1)u^{x-2}e^{-u}\mathrm{d}u\\ &= 0 + (x-1)\Gamma(x-1) \end{align*}\]

베타분포가 normalized임을 증명하기 (\(\int_0^{1}\mathrm{Beta}(\mu\vert a,b)\mathrm{d}\mu = 1\))

\(\int_0^1 \mu^{a-1}(1-\mu)^{b-1}\mathrm{d}\mu = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}\)임을 증명하면 된다.

\[\begin{align*} \Gamma(a)\Gamma(b) &= \int_0^{\infty} x^{a-1}e^{-x}\mathrm{d}x\int_0^{\infty} y^{b-1}e^{-y}\mathrm{d}y\\ &= \int_0^{\infty}\int_0^{\infty}e^{-x-y}x^{a-1}y^{b-1}\mathrm{d}y\mathrm{d}x\\ &= \int_0^{\infty}\int_0^{\infty}e^{-t}x^{a-1}(t-x)^{b-1}\mathrm{d}t\mathrm{d}x &\ \mathrm{by}~ t=y+x, \mathrm{d}t = \mathrm{d}y\\ &= \int_0^{\infty}\int_0^{\infty}e^{-t}x^{a-1}(t-x)^{b-1}\mathrm{d}x\mathrm{d}t\\ &= \int_0^{\infty}e^{-t}\int_0^{\infty}x^{a-1}(t-x)^{b-1}\mathrm{d}x\mathrm{d}t\\ &= \int_0^{\infty}e^{-t}\int_0^1(t\mu)^{a-1}(t-t\mu)^{b-1}t\mathrm{d}\mu\mathrm{d}t &\ \mathrm{by}~ x=t\mu, \mathrm{d}x = t\mathrm{d}\mu\\ &= \int_0^{\infty}e^{-t}t^{a-1}t^{b-1}t\left(\int_0^1 \mu^{a-1}(1-\mu)^{b-1}\mathrm{d}\mu\right)\mathrm{d}t\\ &= \int_0^{\infty}e^{-t}t^{a+b-1}\mathrm{d}t\int_0^1\mu^{a-1}(1-\mu)^{b-1}\mathrm{d}\mu\\ &= \Gamma(a+b)\int_0^1\mu^{a-1}(1-\mu)^{b-1}\mathrm{d}\mu \end{align*}\]

따라서, \(\int_0^1 \mu^{a-1}(1-\mu)^{b-1}\mathrm{d}\mu = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}\)이 성립한다.

기댓값, 분산

• \(\mathbb{E}[\mu] = \frac{a}{a+b}\)
• \(\mathrm{var}[\mu] = \frac{ab}{(a+b)^2(a+b+1)}\)

\(\mu\)의 사후확률 (posterior)

\(l = N-m\) 전체데이터 N에서 m을 뺀 값으로 정의한다.
\(a, b\)는 현재는 확률변수가 아니라 parameter이고 나머지 \(\mu,l,m\)은 확률변수임.

\[\begin{align*} p(\mu \vert m, l, a, b) &= \frac{\textrm{Bin}(m\vert N,\mu)\textrm{Beta}(\mu\vert a,b)}{\int_0^1 \textrm{Bin}(m\vert N,\mu)\textrm{Beta}(\mu\vert a,b)\textrm{d}\mu}\\ &= \frac{\mu^{m+a-1}(1-\mu)^{l+b-1}}{\int_0^1 \mu^{m+b-1}(1-\mu)^{l+b-1}\textrm{d}\mu}\\ &= \frac{\mu^{m+a-1}(1-\mu)^{l+b-1}}{\Gamma(m+a)\Gamma(l+b)/\Gamma(m+a+l+b)}\\ &= \frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)}\mu^{m+a-1}(1-\mu)^{l+b-1} \end{align*}\]

\(\mu\)의 사전확률이 \(a\), \(b\)라는 parameter를 갖고 있다고 하고,
m: x=1인 경우의 관찰횟수
l: x=0인 경우의 관찰횟수
라고 했을 때, 위 식에서 \(\mu\)와 관련된 부분의 의미를 보면,

\(\mu^{m+a-1}(1-\mu)^{l+b-1}\) 여기에서,

\(a\)를 \(m\)만큼 증가시키고, \(b\)를 \(l\)만큼 증가시키는 효과가 나타난다고 볼 수 있다.
데이터 \(m\),\(l\)이 주어지기 전에 가지고 있던 정보는 \(a\), \(b\) 였는데
\(m\),\(l\)이라는 새로운 관찰 결과를 얻은 후에는 \(a\)가 \(m\)만큼 증가하고 \(b\)가 l만큼 증가하는 효과를 가지게 된 것이다.

연속적인 업데이트

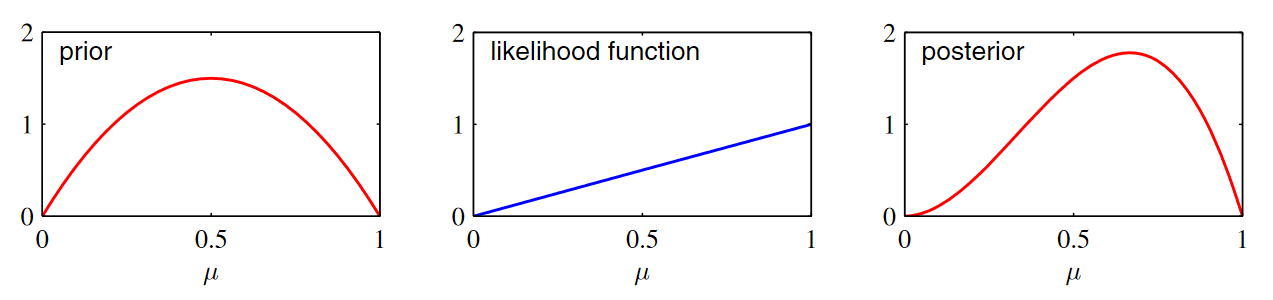
하나의 샘플이 있고 그 값이 1일때의 likelihood

\[Bin(1\vert 1, \mu) = \begin{pmatrix}1 \cr 1 \end{pmatrix} \mu^1(1-\mu)^0 = \mu\]

likelihood 함수는 기울기가 1인 직선형태로 나온다.
사후확률은 prior x likelihood 인 형태로 나올 것이다.
두 함수를 곱하고 normalize했을 때 위와 같은 posterior 모습을 보인다.

새로운 데이터가 들어올 때에는 지금은 \(\mu\)에 대한 사후확률이지만 다음번에 새로운 데이터에 적용될 때에는
\(\mu\)에 대한 사전확률로 사용되면서 새로운 데이터를 통해서 \(\mu\)에 대한 정보가 계속 업데이트 되는 것이다.
데이터가 새롭게 들어올때마다 정보가 업데이트 된다는 의미이다.

예측분포 (predictive distribution)

parameter를 구한 다음 예측 분포를 구한다.

\[p(x=1 \vert \mathcal{D}) = \int_0^1 p(x=1\vert \mu)p(\mu\vert \mathcal{D})\mathrm{d}\mu = \int_0^1 \mu p(\mu\vert \mathcal{D})\mathrm{d}\mu = \mathbb{E}[\mu\vert \mathcal{D}]\] \[p(x=1 \vert \mathcal{D}) = \frac{m+a}{m+a+l+b}\]

다항변수(Multinomial Variables): 빈도주의 방법

\(K\)개의 상태를 가질 수 있는 확률변수를 \(K\)차원의 벡터 \(\mathbf{x}\) (하나의 원소만 1이고 나머지는 0)로 나타낼 수 있다. 이런 \(\mathbf{x}\)를 위해서 베르누이 분포를 다음과 같이 일반화시킬 수 있다.

\[p(\mathbf{x}\vert \pmb \mu) = \prod_{k=1}^K \mu_k^{x_k}\]

with \(\sum_k \mu_k = 1\)

\(\mathbf{x}\)의 기댓값

\[\mathbb{E}[\mathbf{x}\vert \pmb \mu] = \sum_{\mathbf{x}} p(\mathbf{x}\vert \pmb \mu) = (\mu_1,\ldots,\mu_M)^T = \pmb \mu\]

우도함수

\(\bf x\)값을 \(N\)번 관찰한 결과 \(\mathcal{D} = \{\bf x_1,\ldots,\bf x_N\}\)가 주어졌을 때, 우도함수는 다음과 같다.

\[p(\mathcal{D}\vert \pmb \mu) = \prod_{n=1}^N\prod_{k=1}^K \mu_k^{x_{nk}} = \prod_{k=1}^K \mu_k^{(\sum_n x_{nk})} = \prod_{k=1}^K \mu_k^{m_k}\] \[m_k = \sum_n x_{nk}\]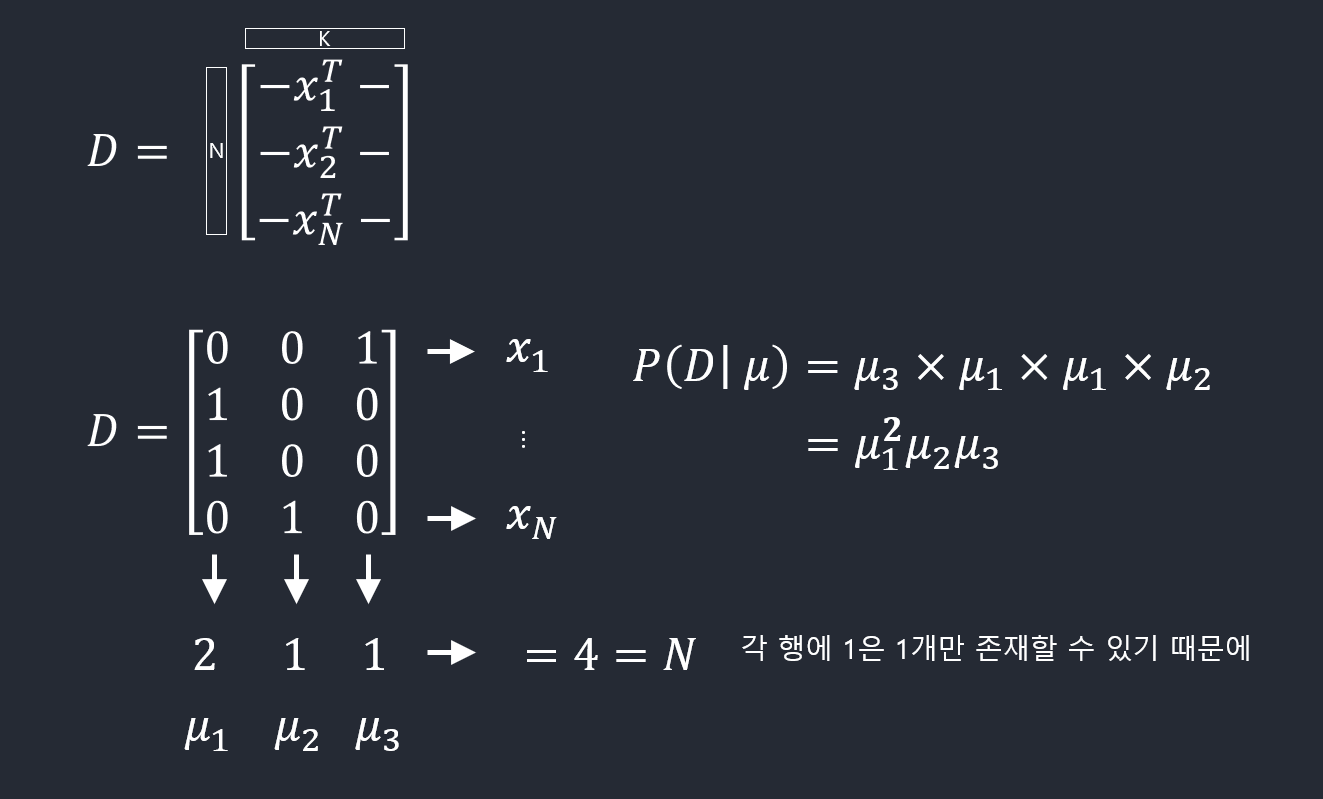

MLE

\(\mu\)의 최대우도 추정치(maximum likelihood estimate)를 구하기 위해선 \(\mu_k\)의 합이 1이 된다는 조건하에서 \(\ln p(\mathcal{D}\vert \pmb \mu)\)을 최대화시키는 \(\mu_k\)를 구해야 한다. 라그랑주 승수(Lagrange multiplier) \(\lambda\)를 사용해서 다음을 최대화시키면 된다.

\[\sum_{k=1}^K m_k \ln \mu_k + \lambda \left(\sum_{k=1}^K \mu_k -1\right)\] \[\mu_k^{ML} = \frac{m_k}{N}\]

Constraint Optimization 문제이기 때문에 라그랑주 방법을 사용한다.
Equality Condition이기 때문에 lambda를 붙여준다(+ or – 관계 없다.)
\(\mu_𝑘\) 가 어떨때 우도함수가 최대화 되는지를 구한다.

라그랑주를 활용한 식 전체에 대해 \(\mu_𝑘\) 에 관해서 미분을 한다.
그 결과를 0으로 놓고 \(\mu_𝑘\)에 대해 풀면 된다.

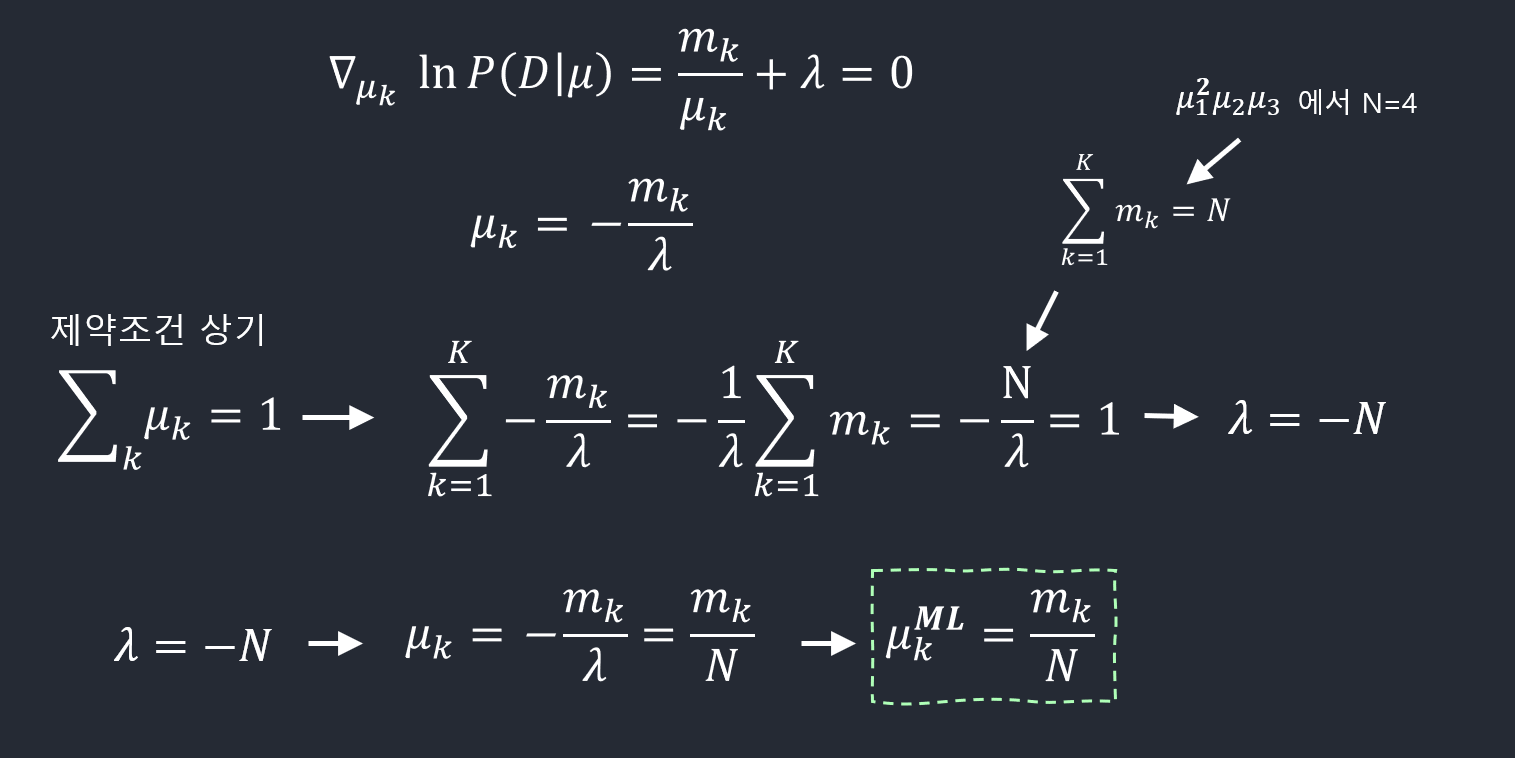
라그랑주가 뭔지 여기에 적을 것

다항변수(Multinomial Variables): 베이지언 방법

다항분포 (Multinomial distribution)

파라미터 \(\pmb \mu\)와 전체 관찰개수 \(N\)이 주어졌을 때 \(m_1,\ldots,m_K\)의 분포를 다항분포(multinomial distribution)이라고 하고 다음과 같은 형태를 가진다.

\[\mathrm{Mult}(m_1,\ldots,m_K\vert \pmb \mu,N) = {N \choose m_1m_2\ldots m_K} \prod_{k=1}^K \mu_k^{m_k}\] \[{N \choose m_1m_2\ldots m_K} = \frac{N!}{m_1!m_2!\ldots m_K!}\] \[\sum_{k=1}^K m_k= N\]

\({N \choose m_1m_2\ldots m_K}\): N개의 물체가 있을 때, 각각의 사이즈가 \(m_1m_2\ldots m_K\) 가 되는 k개의 그룹으로 만들 수 있는 모든 경우의 수를 의미

디리클레 분포(Dirichlet distribution): 다항분포를 위한 켤레사전분포

이항변수를 위해 사용했던 베타분포를 일반화시킨 형태

\[\mathrm{Dir}(\pmb \mu\vert \mathbf{\alpha}) = \frac{\Gamma{\alpha_0}}{\Gamma(\alpha_1)\ldots\Gamma(\alpha_K)}\prod_{k=1}^K \mu_k^{\alpha_k-1}\] \[\alpha_0 = \sum_{k=1}^K \alpha_k\]

디리클레 분포의 normalization 증명 (\(K=3\))

다음 결과를 사용한다.
\(\begin{align*} \int_L^U(x-L)^{a-1}(U-x)^{b-1}\mathrm{d}x &= \int_0^1 (U-L)^{a-1}t^{a-1}(U-L)^{b-1}(1-t)^{b-1}(U-L)\mathrm{d}t &\ \mathrm{by}~ t=\frac{x-L}{U-L}\\ &= (U-L)^{a+b-1}\int_0^1 t^{a-1}(1-t)^{b-1}\mathrm{d}t\\ &= (U-L)^{a+b-1}\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} \end{align*}\)

\[\begin{align*} \int_0^{1-\mu_1}\mu_1^{\alpha_1-1}\mu_2^{\alpha_2-1}(1-\mu_1-\mu_2)^{\alpha_3-1}\mathrm{d}\mu_2 &= \mu_1^{\alpha_1-1}\int_0^{1-\mu_1}\mu_2^{\alpha_2-1}(1-\mu_1-\mu_2)^{\alpha_3-1}\mathrm{d}\mu_2 &\ \textrm{by}~ L=0, U=1-\mu_1\\ &= \mu_1^{\alpha_1-1}(1-\mu_1)^{\alpha_2+\alpha_3-1}\frac{\Gamma(\alpha_2)\Gamma(\alpha_3)}{\Gamma(\alpha_2+\alpha_3)} \end{align*}\] \[\begin{align*} \int_0^1\int_0^{1-\mu_1}\mu_1^{\alpha_1-1}\mu_2^{\alpha_2-1}(1-\mu_1-\mu_2)^{\alpha_3-1}\mathrm{d}\mu_2\mathrm{d}\mu_1 &= \frac{\Gamma(\alpha_2)\Gamma(\alpha_3)}{\Gamma(\alpha_2+\alpha_3)} \int_0^1 \mu_1^{\alpha_1-1}(1-\mu_1)^{\alpha_2+\alpha_3-1}\mathrm{d}\mu_1\\ &= \frac{\Gamma(\alpha_2)\Gamma(\alpha_3)}{\Gamma(\alpha_2+\alpha_3)} \frac{\Gamma(\alpha_1)\Gamma(\alpha_2+\alpha_3)}{\Gamma(\alpha_1+\alpha_2+\alpha_3)}\\ &= \frac{\Gamma(\alpha_1)\Gamma(\alpha_2)\Gamma(\alpha_3)}{\Gamma(\alpha_1+\alpha_2+\alpha_3)} \end{align*}\]

일반적인 경우(k=M): 귀납법(induction)으로 증명

base 경우가 성립한다는 것을 보여주고 N-1인 경우에 성립을 한다고 가정할 때,
N인 경우에 성립한다는 것을 보여주면 모든 N에 대해서 성립한다는 것.

base: M=2 인 베타분포에서 성립
M-1개의 변수들이 있을때 성립하면
M개에 대해서도 성립한다는 것을 보여주면 된다.

M개의 변수들 \(\mu_1 \sim \mu_𝑀\)
\(\mu_1+…+\mu_{𝑀−1} \le 1\) 이것을 만족시키면 된다.
이 식을 만족시키는 적분식은

\(\mu\)의 사후확률 (posterior)

\[\begin{align*} p(\pmb \mu\vert \mathcal{D},\mathbf{\alpha}) &= \mathrm{Dir}(\pmb \mu\vert \mathbf{\alpha}+\mathbf{m})\\ &= \frac{\Gamma(\alpha_0+N)}{\Gamma(\alpha_1+m_1)\ldots\Gamma(\alpha_K+m_K)}\prod_{k=1}^K \mu_k^{\alpha_k+m_k-1} \end{align*}\] \[\mathbf{m} = (m_1,\ldots,m_K)^T\]

\(\alpha_k\)를 \(x_k=1\)에 대한 사전관찰 개수라고 생각할 수 있다.

In [ ]:

# for inline plots in jupyter
%matplotlib inline
# import matplotlib
import matplotlib.pyplot as plt
# for latex equations
from IPython.display import Math, Latex
# for displaying images
from IPython.core.display import Image

In [ ]:

# import seaborn
import seaborn as sns
# settings for seaborn plotting style
sns.set(color_codes=True)
# settings for seaborn plot sizes
sns.set(rc={'figure.figsize':(5,5)})
import numpy as np

Uniform Distribution
In [ ]:

# import uniform distribution
from scipy.stats import uniform

In [ ]:

# random numbers from uniform distribution
n = 10000
start = 10
width = 20
data_uniform = uniform.rvs(size=n, loc = start, scale=width)

In [ ]:

data_uniform

In [ ]:

ax = sns.distplot(data_uniform,
                  bins=100,
                  kde=True,
                  color='skyblue',
                  hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Uniform Distribution ', ylabel='Frequency')

Bernoulli Distribution
In [ ]:

from scipy.stats import bernoulli
data_bern = bernoulli.rvs(size=10000,p=0.8)

In [ ]:

np.unique(data_bern, return_counts=True)

In [ ]:

ax= sns.distplot(data_bern,
                 kde=False,
                 color="skyblue",
                 hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Bernoulli Distribution', ylabel='Frequency')

Beta Distribution
In [ ]:

from scipy.stats import beta
a, b = 0.1, 0.1
data_beta = beta.rvs(a, b, size=10000)

In [ ]:

data_beta

In [ ]:

ax= sns.distplot(data_beta,
                 kde=False,
                 color="skyblue",
                 hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta Distribution', ylabel='Frequency')

Multinomial Distribution
In [ ]:

from scipy.stats import multinomial
data_multinomial = multinomial.rvs(n=1, p=[0.2, 0.1, 0.3, 0.4], size=10000)

In [ ]:

data_multinomial[:50]

In [ ]:

for i in range(4):
  print(np.unique(data_multinomial[:,i], return_counts=True))

Appendix

MathJax

Matrix with parenthesis \(\begin{pmatrix}1 \cr 1 \end{pmatrix}\):

$$\begin{pmatrix}1 \cr 1 \end{pmatrix}$$

References

Pattern Recognition and Machine Learning: https://tensorflowkorea.files.wordpress.com/2018/11/bishop-pattern-recognition-and-machine-learning-2006.pdf