NN basics - ML Intro
To do
Gradient Boost
XGBoost
Sources
- 기계학습, 오일석
- Machine Learning: a Probabilistic Perspective by K. Murphy
- Deep Learning by Goodfellow, Bengio and Courville
- stanford cs231n
Prerequisites
- Linear Algebra
- Probaility and Statistics
- Information Theory
데이터 영역 공간은 높아지는데 어떻게 높은 성능을 달성하는가?
그 안의 데이터는 적어짐에도 불구하고.
데이터 희소특성 가정
Mnist를 예로들면, 28 by 28의 공간에서 모든 영역에서 데이터가 발생하는 것은 아님.
희소한 영역에서 발생할 것임.
\(2^784\) 공간 안에서 일부 희소한 공간에서 유의미한 데이터가 발생함.
매니폴드 가정
사진과 같은 고차원의 데이터는 그 안의 내재되어 있는 규칙에 따르면, 유사하게 묶여 있는 부분이 많음.
고차원의 데이터는 낮은 차원으로 데이터를 투영해도 그 규칙은 보존되어야 한다는 점
랜덤한 노이즈는 smooth함이 없기 때문에 유사성이 저차원에서 보존이 되지 않음. 따라서 희소한 데이터를 가지고 있어도 학습이 안됨.
원래 차원의 저주 때문에 학습이 잘 이루어지지 않아야 하지만, 그 내에서 특정한 규칙들에 의해 유사함이 보존됨.
Although there is a formal mathematical meaning to the term “manifold,” in machine learning it tends to be used more loosely to designate a connected set of points that can be approximated well by considering only a small number of degrees of freedom, or dimensions, embedded in a higher-dimensional space. Each dimension corresponds to a local direction of variation. (Deep Learning, By Ian Goodfellow, Yoshua Bengio and Aaron Courville)
smoothness in manifold
Smoothness:
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over some domain. At the very minimum, a function could be considered “smooth” if it is differentiable everywhere (hence continuous). At the other end, it might also possess derivatives of all orders in its domain, in which case it is said to be infinitely differentiable and referred to as a C-infinity function (or \(C^{\infty}\) function). wikipedia
Manifold Learning (from. 오토인코더의 모든 것)
Manifold란 고차원 데이터(e.g Image의 경우 (256, 256, 3) or…)가 있을 때 고차원 데이터를 데이터 공간에 뿌리면 sample들을 잘 아우르는 subspace가 있을 것이라는 가정에서 학습을 진행하는 방법 이렇게 찾은 manifold는 데이터의 차원을 축소시킬 수 있음.
Usage of Manifold Learning
-
- Data Compression
- Noisy Image Compression
- Data Compression
-
- Data Visualization
- t-sne
- Data Visualization
-
- Curse of dimensionality (Manifold Hypothesis)
- 데이터의 차원이 증가할수록 해당 공간의 크기(부피)는 기하급수적으로 증가하기 때문에 동일한 개수의 데이터의 밀도는 차원이 증가할수록 급속도로 희박해지게 됨
- 따라서 차원이 증가할수록 데이터 분포 분석 또는 모델 추정에 필요한 샘플 데이터의 개수가 기하급수적으로 증가하게 됨. Manifold Hypothesis
- Natural data in high dimensional spaces concentrates close to lower dimensional manifolds. (고차원 데이터의 밀도는 낮지만, 이들의 집합을 포함하는 저차원의 매니폴드가 있다.)
- Probability density decreases very rapidly when moving away from the supporting manifold. (이 저차원의 매니폴드를 벗어나는 순간 급격히 밀도는 낮아진다.)
- Curse of dimensionality (Manifold Hypothesis)
-
- Discovering most important features (Reasonable distance metric, Needs disentangling the underlying explanatory factors)
- Manifold follows naturally from continuous underlying factors (\(\approx\) intrinsic manifold coordinates)
- Such continuous factors are part of a meaningful representation.
- Resonable distance metric
- 의미적으로 가깝다고 생각되는 고차원 공간에서의 두 샘플들 간의 거리는 먼 경우가 많다.
- 고차원 공간에서 가까운 두 샘플들은 의미적으로는 굉장히 다를 수 있다.
- 차원의 저주로 인해 고차원에서의 유의미한 거리 측정 방식을 찾기 어렵다.
- Needs disentangling the underlying explanatory factors. - In general, learned manifold is entangled, i.e. encoded in a data space in a complicated manner. When a manifold is disentangled, it would be more interpretable and easier to apply to tasks.
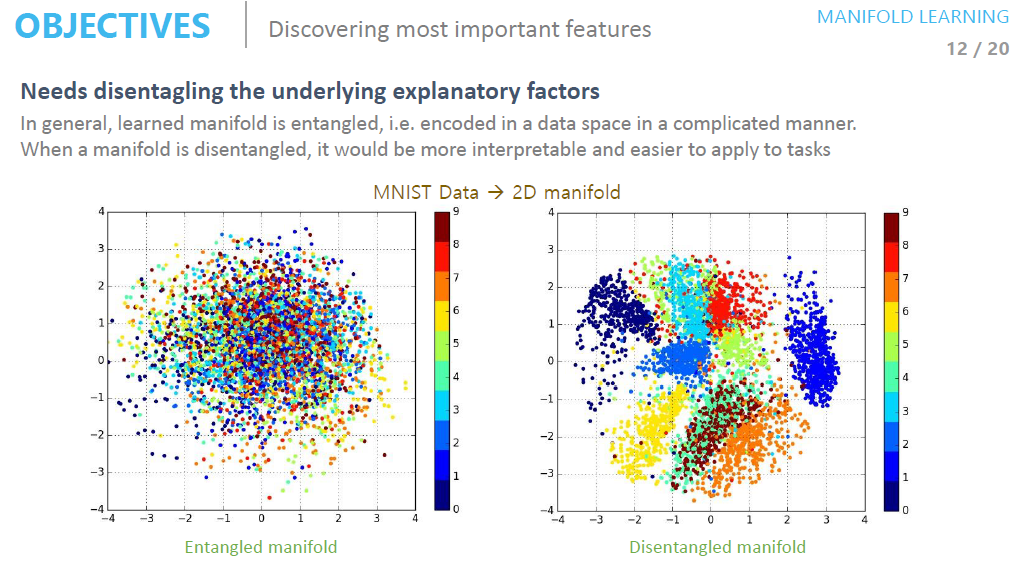
- Discovering most important features (Reasonable distance metric, Needs disentangling the underlying explanatory factors)
Types of Dimensionality Reduction
- Linear
- PCA
- LDA
- etc..
- Non-Linear
- Autoencoders(AE)
- t-SNE
- Isomap
- LLE(Locally-linear embedding)
- etc..
Manifold란?
이미지를 구성하는 픽셀, 화소를 하나의 차원으로 간주하여 우리는 고차원 공간에 한 점으로 이미지를 매핑시킬 수 있습니다. 내가 가진 학습 데이터셋에 존재하는 수많은 이미지를 고차원 공간 속에 매핑시키면 유사한 이미지는 특정 공간에 모여있을 것입니다. 이 내용과 관련한 좋은 시각화 자료는 여기를 참고하시기 바랍니다. 그리고 그 점들의 집합을 잘 아우르는 전체 공간의 부분집합(subspace)이 존재할 수 있을텐데 그것을 우리는 매니폴드(manifold)라고 합니다.
우선 매니폴드는 다음과 같은 특징을 가지고 있습니다.
Natural data in high dimensional spaces concentrates close to lower dimensional manifolds.
고차원 데이터의 밀도는 낮지만, 이들의 집합을 포함하는 저차원의 매니폴드가 있다.Probability density decreases very rapidly when moving away from the supporting manifold.
이 저차원의 매니폴드를 벗어나는 순간 급격히 밀도는 낮아진다.
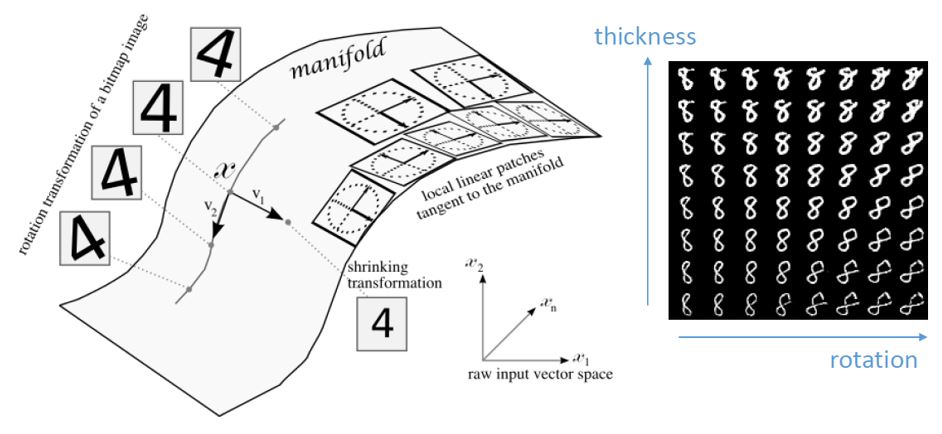
매니폴드 공간은 본래 고차원 공간의 subspace이기 때문에 차원수가 상대적으로 작아집니다. 이는 데이터 차원 축소(dimension reduction)를 가능하게 합니다. 그리고 차원 축소가 잘 되었다는 것은 매니폴드 공간을 잘 찾았다는 것이기도 합니다. 본래 고차원 공간에서 각 차원들을 잘 설명하는 새로운 특징(feature)을 축으로 하는 공간을 찾았다는 뜻으로 해석할수도 있습니다. 아래 그림을 예시로 살펴보겠습니다.
유명한 MNIST 데이터셋은 784차원 이미지 데이터입니다. 이를 2차원으로 축소하였을 때 한 축은 두께를 조절하고 한 축은 회전을 담당함을 볼 수 있습니다. 매니폴드 공간에서 두 개의 축은 두 개의 특징(feature)를 의미하고 이를 변경하였을 때 변화되는 이미지 형태를 획득할 수 있습니다. 매니폴드 공간은 이렇게 의미론적 유사성을 나타내는 공간으로 해석할 수 있습니다. 이는 또 어떤 이점이 있을까요?
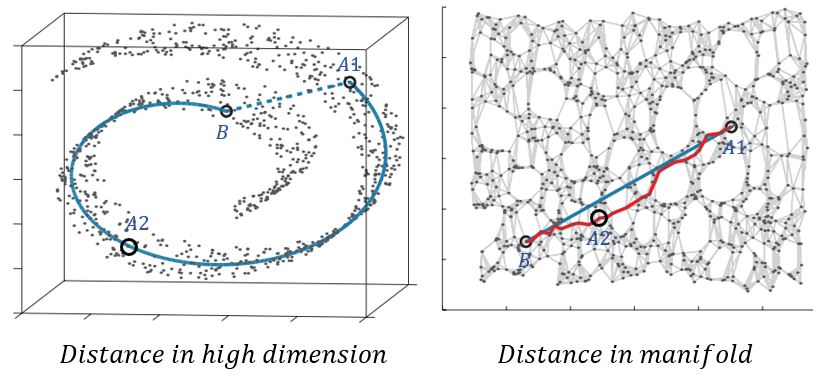
공간속에서 매핑된 데이터들이 얼마나 유사한지 측정하는 방법에는 거리를 재는 방법이 있습니다. 유클리디안 거리를 통해 가장 가까운 점들이 나와 가장 유사하고 생각하는 방법입니다. 그러나 고차원 공간상에서 나와 가까운 점이 실제로 나와 유사하지 않을 수 있다는 관점은 매니폴드로 설명할 수 있습니다. 아래 그림을 살펴보겠습니다.
고차원 공간에서 B와 A1 거리가 A2 거리보다 가깝습니다. 그러나 매니폴드 공간에서는 A2가 B에 더 가깝습니다. 이미지 데이터 픽셀 간 거리는 A1,B가 더 가까울 수 있으나 의미적인 유사성 관점에서는 A2,B가 더 가까울 수 있는 것입니다. 근처에 있는 점이 나랑 유사하다고 생각했지만 실제로는 아닐 수 있는 예시가됩니다. 이것을 실제 이미지로 확인한다면 어떻게 될까요?
자세히보면 고차원 공간에서 이미지는 팔이 2개 골프채가 2개로 좌우 이미지의 픽셀 중간모습을 보여줍니다. 이것은 우리가 원하는 사진이 아닙니다. 반대로 매니폴드 공간에서 중간값은 공을 치는 중간과정 모습, 의미적으로 중간에 있는 모습을 보여줍니다. 우리가 원하는 것도 사실 이것이라고 할 수 있겠지요. 매니폴드를 잘 찾으면 의미적인 유사성을 잘 보존할 수 있습니다. 또한 유사한 데이터를 획득하여 학습 데이터에 없는 데이터를 획득할 가능성도 열리게됩니다.
Bootstrap
Sampling with replacement
데이터 분포가 불균형일 때 적용
주로 이상탐지나 보안의 태스크에 적용 (클래스 imbalance가 심한 태스크)
Appendix
Reference
Manifold Learning: https://deepinsight.tistory.com/124
Manifold Learning slides: https://www.slideshare.net/NaverEngineering/ss-96581209
manifold: https://kh-mo.github.io/notation/2019/03/10/manifold_learning/
Gradient Boost: https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-15-Gradient-Boost
Bagging & Boosting: https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-11-%EC%95%99%EC%83%81%EB%B8%94-%ED%95%99%EC%8A%B5-Ensemble-Learning-%EB%B0%B0%EA%B9%85Bagging%EA%B3%BC-%EB%B6%80%EC%8A%A4%ED%8C%85Boosting
[Paper Review] XGBoost: A Scalable Tree Boosting System:https://youtu.be/VkaZXGknN3g
XGBoost Part 1 (of 4): Regression: https://youtu.be/OtD8wVaFm6E
Gradient Boost Part 1 (of 4): Regression Main Ideas: https://youtu.be/3CC4N4z3GJc


Leave a comment