ML basics - Linear Algebra

왜 선형대수를 알아야 하는가?

Deep learning을 이해하기 위해서 반드시 선형대수 + 행렬미분 + 확률의 탄탄한 기초가 필요하다.

예) Transformer의 attention matrix:

\[\mathrm{Att}_{\leftrightarrow}(Q, K, V) = D^{-1}AV, {\sim}A = \exp(QK^T/\sqrt{d}), {\sim}D = \mathrm{diag}(A1_L)\]

이렇게 핵심 아이디어가 행렬에 관한 식으로 표현되는 경우가 많다.

목표: 선형대수와 행렬미분의 기초를 배우고 간단한 머신러닝 알고리즘(PCA)을 유도해보고자 한다.

기본 표기법 (Basic Notation)

• \(A\in \mathbb{R}^{m\times n}\)는 \(m\)개의 행과 \(n\)개의 열을 가진 행렬을 의미한다.
• \(x \in \mathbb{R}^n\)는 \(n\)개의 원소를 가진 벡터를 의미한다. \(n\)차원 벡터는 \(n\)개의 행과 1개의 열을 가진 행렬로 생각할 수도 있다. 이것을 열벡터(column vector)로 부르기도 한다. 만약, 명시적으로 행벡터(row vector)를 표현하고자 한다면, \(x^T\)(\(T\)는 transpose를 의미)로 쓴다.
• 벡터 \(x\)의 \(i\)번째 원소는 \(x_i\)로 표시한다.

\[\begin{align*} x = \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} \end{align*}\]

• \(a_{ij}\)(또는 \(A_{ij}, A_{i,j}\))는 행렬 \(A\)의 \(i\)번째 행, \(j\)번째 열에 있는 원소를 표시한다.

\[\begin{align*} A = \begin{bmatrix} a_{11} &\ a_{12} &\ \cdots &\ a_{1n}\\ a_{21} &\ a_{22} &\ \cdots &\ a_{2n}\\ \vdots &\ \vdots &\ \ddots &\ \vdots\\ a_{m1} &\ a_{m2} &\ \cdots &\ a_{mn} \end{bmatrix} \end{align*}\]

• \(A\)의 \(j\)번째 열을 \(a_j\) 혹은 \(A_{:,j}\)로 표시한다.

\[\begin{align*} A = \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ a_1 &\ a_2 &\ \cdots &\ a_n\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} \end{align*}\]

• \(A\)의 \(i\)번째 행을 \(a_i^T\) 혹은 \(A_{i,:}\)로 표시한다.

\[\begin{align*} A = \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_m^T & - \end{bmatrix} \end{align*}\]

Python에서의 벡터, 행렬 표현방법:

In [1]: [10.5, 5.2, 3.25, 7.0]
Out[1]: [10.5, 5.2, 3.25, 7.0]

In [2]: import numpy as np
        x = np.array([10.5, 5.2, 3.25])

In [3]: x.shape
Out[3]: (3,)

In [4]: i = 2
        x[i]
Out[4]: 3.25

In [5]: np.expand_dims(x, axis=1).shape
Out[5]: (3, 1)

In [6]: A = np.array([
            [10,20,30],
            [40,50,60]
        ])
        A
Out[6]: array([[10, 20, 30],
             [40, 50, 60]])

In [7]: A.shape
Out[7]: (2, 3)

In [8]: i = 0
        j = 2
        A[i, j]
Out[8]: 30

In [9]: # column vector
        j = 1
        A[:, j]
Out[9]: array([20, 50])

In [10]:# row vector
        i = 1
        A[i, :]
Out[10]:array([40, 50, 60])

행렬의 곱셉 (Matrix Multiplication)

두 개의 행렬 \(A\in \mathbb{R}^{m\times n}\), \(B\in \mathbb{R}^{n\times p}\)의 곱 \(C = AB \in \mathbb{R}^{m\times p}\)는 다음과 같이 정의된다.

\[C_{ij} = \sum_{k=1}^n A_{ik}B_{kj}\]

행렬의 곱셈을 이해하는 몇 가지 방식들

• 벡터 \(\times\) 벡터
• 행렬 \(\times\) 벡터
• 행렬 \(\times\) 행렬

벡터 \(\times\) 벡터 (Vector-Vector Products)

내적(inner product or dot product)

두 개의 벡터 \(x, y\in \mathbb{R}^n\)이 주어졌을 때 내적(inner product 또는 dot product) \(x^Ty\)는 다음과 같이 정의된다.

\[\begin{align*} x^Ty \in \mathbb{R} = [\mbox{ }x_1\mbox{ }x_2\mbox{ }\cdots \mbox{ }x_n\mbox{ }] \begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_n \end{bmatrix} = \sum_{i=1}^n x_i y_i \end{align*}\] \[x^Ty = y^Tx\]

In [11]:import numpy as np
        x = np.array([1, 2, 3])
        y = np.array([4, 5, 6])
        x.dot(y)
Out[11]:32

In [12]:y.dot(x)
Out[12]:32

외적(outer product)

두 개의 벡터 \(x\in \mathbb{R}^m, y\in \mathbb{R}^n\)이 주어졌을 때 외적(outer product) \(xy^T\in \mathbb{R}^{m\times n}\)는 다음과 같이 정의된다.

\[\begin{align*} xy^T \in \mathbb{R}^{m\times n} = \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_m \end{bmatrix} [\mbox{ }y_1\mbox{ }y_2\mbox{ }\cdots \mbox{ }y_n\mbox{ }] = \begin{bmatrix} x_1y_1 &\ x_1y_2 &\ \cdots &\ x_1y_n\\ x_2y_1 &\ x_2y_2 &\ \cdots &\ x_2y_n\\ \vdots &\ \vdots &\ \ddots &\ \vdots\\ x_my_1 &\ x_my_2 &\ \cdots &\ x_my_n \end{bmatrix} \end{align*}\]

In [13]:x = np.array([1, 2, 3])
        y = np.array([4, 5, 6])

In [14]:x = np.expand_dims(x, axis=1)
        y = np.expand_dims(y, axis=0)
        x.shape, y.shape
Out[14]:((3, 1), (1, 3))

In [15]:np.matmul(x,y)
Out[15]:array([[ 4,  5,  6],
                [ 8, 10, 12],
                [12, 15, 18]])

외적이 유용한 경우.
아래 행렬 \(A\)는 모든 열들이 동일한 벡터 \(x\)를 가지고 있다.
외적을 이용하면 간편하게 \(x\mathbf{1}^T\)로 나타낼 수 있다 (\(\mathbf{1}\in \mathbb{R}^n\)는 모든 원소가 1인 \(n\)차원 벡터).

\[\begin{align*} A = \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ x &\ x &\ \cdots &\ x\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} = \begin{bmatrix} x_1 &\ x_1 &\ \cdots &\ x_1\\ x_2 &\ x_2 &\ \cdots &\ x_2\\ \vdots &\ \vdots &\ \ddots &\ \vdots\\ x_m &\ x_m &\ \cdots &\ x_m \end{bmatrix} = \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_m \end{bmatrix} \begin{bmatrix} 1 &\ 1 &\ \cdots &\ 1 \end{bmatrix} = x\mathbf{1}^T \end{align*}\]

In [16]:# column vector
        x = np.expand_dims(np.array([1, 2, 3]), axis=1)

In [17]:ones = np.ones([1,4])

In [18]:A = np.matmul(x, ones)
        A
Out[18]:array([[1., 1., 1., 1.],
                [2., 2., 2., 2.],
                [3., 3., 3., 3.]])

행렬 \(\times\) 벡터 (Matrix-Vector Products)

행렬 \(A\in \mathbb{R}^{m\times n}\)와 벡터 \(x\in \mathbb{R}^n\)의 곱은 벡터 \(y = Ax \in \mathbb{R}^m\)이다.
이 곱을 몇 가지 측면에서 바라볼 수 있다.
열벡터를 오른쪽에 곱하고(\(Ax\)), \(A\)가 행의 형태로 표현되었을 때

\[\begin{align*} y = Ax = \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_m^T & - \end{bmatrix} x = \begin{bmatrix} a_1^Tx\\ a_2^Tx\\ \vdots\\ a_m^Tx \end{bmatrix} \end{align*}\]

In [19]:A = np.array([
            [1,2,3],
            [4,5,6]
        ])
        A
Out[19]:array([[1, 2, 3],
                [4, 5, 6]])

In [20]:ones = np.ones([3,1])

In [21]:np.matmul(A, ones)
Out[21]:array([[ 6.],
                [15.]])

열벡터를 오른쪽에 곱하고(\(Ax\)), \(A\)가 열의 형태로 표현되었을 때

\[\begin{align*} y = Ax = \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ a_1 &\ a_2 &\ \cdots &\ a_n\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} \vert\\ a_1\\ \vert \end{bmatrix} x_1 + \begin{bmatrix} \vert\\ a_2\\ \vert \end{bmatrix} x_2 + \cdots + \begin{bmatrix} \vert\\ a_n\\ \vert \end{bmatrix} x_n \end{align*}\]

In [22]:A = np.array([
            [1,0,1],
            [0,1,1]
        ])
        x = np.array([
            [1],
            [2],
            [3]
        ])
        np.matmul(A, x)
Out[22]:array([[4],
                [5]])

In [23]:for i in range(A.shape[1]):
            print('a_'+str(i)+':', A[:,i], '\tx_'+str(i)+':', x[i], '\ta_'+str(i)+'*x_'+str(i)+':', A[:,i]*x[i])
Out[23]:a_0: [1 0] 	x_0: [1] 	a_0*x_0: [1 0]
        a_1: [0 1] 	x_1: [2] 	a_1*x_1: [0 2]
        a_2: [1 1] 	x_2: [3] 	a_2*x_2: [3 3]

행벡터를 왼쪽에 곱하고(\(x^TA\)), \(A\)가 열의 형태로 표현되었을 때

\(A\in \mathbb{R}^{m\times n}\), \(x\in \mathbb{R}^m\), \(y\in \mathbb{R}^n\)일 때, \(y^T = x^TA\)

\[\begin{align*} y^T = x^TA = x^T \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ a_1 &\ a_2 &\ \cdots &\ a_n\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} = \begin{bmatrix} x^Ta_1 &\ x^Ta_2 &\ \cdots &\ x^Ta_n \end{bmatrix} \end{align*}\]

행벡터를 왼쪽에 곱하고(\(x^TA\)), \(A\)가 행의 형태로 표현되었을 때

\[\begin{align*} y^T =&\ x^TA\\ =&\ \begin{bmatrix} x_1 & x_2 & \cdots & x_m \end{bmatrix} \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_m^T & - \end{bmatrix}\\ =&\ x_1 \begin{bmatrix} - & a_1^T & - \end{bmatrix} + x_2 \begin{bmatrix} - & a_2^T & - \end{bmatrix} + \cdots + x_n \begin{bmatrix} - & a_n^T & - \end{bmatrix} \end{align*}\]

행렬 \(\times\) 행렬 (Matrix-Matrix Products)

행렬 \(\times\) 행렬 연산도 몇 가지 관점으로 접근할 수 있다. 일련의 벡터 \(\times\) 벡터 연산으로 표현하는 경우

\(A\)와 \(B\)가 행 또는 열로 표현되었는가에 따라 두 가지 경우로 나눌 수 있다.

\(A\)가 행으로 \(B\)가 열로 표현되었을 때
\(\begin{align*} C = AB = \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_m^T & - \end{bmatrix} \begin{bmatrix} \vert & \vert & & \vert\\ b_1 & b_2 & \cdots & b_p\\ \vert & \vert & & \vert \end{bmatrix} = \begin{bmatrix} a_1^Tb_1 & a_1^Tb_2 & \cdots & a_1^Tb_p\\ a_2^Tb_1 & a_2^Tb_2 & \cdots & a_2^Tb_p\\ \vdots & \vdots & \ddots & \vdots\\ a_m^Tb_1 & a_m^Tb_2 & \cdots & a_m^Tb_p\\ \end{bmatrix} \end{align*}\)

\(A\in \mathbb{R}^{m\times n}\), \(B\in \mathbb{R}^{n\times p}\), \(a_i \in \mathbb{R}^n\), \(b_j \in \mathbb{R}^n\)이기 때문에 내적값들이 자연스럽게 정의된다.

\(A\)가 열로 \(B\)가 행으로 표현되었을 때
위보다는 까다롭지만 가끔씩 유용하다.

\[\begin{align*} C = AB = \begin{bmatrix} \vert & \vert & & \vert\\ a_1 & a_2 & \cdots & a_n\\ \vert & \vert & & \vert \end{bmatrix} \begin{bmatrix} - & b_1^T & -\\ - & b_2^T & -\\ & \vdots &\\ - & b_n^T & - \end{bmatrix} = \sum_{i=1}^n a_i b_i^T \end{align*}\]

\(AB\)는 모든 \(i\)에 대해서 \(a_i\in \mathbb{R}^m\)와 \(b_i\in \mathbb{R}^p\)의 외적의 합이다.
\(a_i b_i^T\)의 차원은 \(m\times p\)이다 (\(C\)의 차원과 동일).
일련의 행렬 \(\times\) 벡터 연산으로 표현하는 경우

\(B\)가 열로 표현되었을 때

\(C=AB\)일 때 \(C\)의 열들을 \(A\)와 \(B\)의 열들의 곱으로 나타낼 수 있다.

\[\begin{align*} C = AB = A \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ b_1 &\ b_2 &\ \cdots &\ b_p\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} = \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ Ab_1 &\ Ab_2 &\ \cdots &\ Ab_p\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} \end{align*}\]

각각의 \(c_i = Ab_i\)는 앞에서 살펴본 행렬 \(\times\) 벡터의 두 가지 관점으로 해석할 수 있다.

\(A\)가 행으로 표현되었을 때

\[\begin{align*} C = AB = \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_m^T & - \end{bmatrix} B = \begin{bmatrix} - & a_1^TB & -\\ - & a_2^TB & -\\ & \vdots &\\ - & a_m^TB & - \end{bmatrix} \end{align*}\]

중요 연산과 성질들 (Operations and Properties)

정방(Square), 삼각(triangular), 대각(diagonal), 단위(identity) 행렬들

정방행렬(square matrix): 행과 열의 개수가 동일

\(\begin{bmatrix} 4 &\ 9 &\ 2 \\ 3 &\ 5 &\ 7 \\ 8 &\ 1 &\ 6 \end{bmatrix}\)

상삼각행렬(upper triangular matrix): 정방행렬이며 주대각선 아래 원소들이 모두 0

\(\begin{bmatrix} 4 &\ 9 &\ 2 \\ 0 &\ 5 &\ 7 \\ 0 &\ 0 &\ 6 \end{bmatrix}\)

하삼각행렬(lower triangular matrix): 정방행렬이며 주대각선 위 원소들이 모두 0

\(\begin{bmatrix} 4 &\ 0 &\ 0 \\ 3 &\ 5 &\ 0 \\ 8 &\ 1 &\ 6 \end{bmatrix}\)

대각행렬(diagonal matrix): 정방행렬이며 주대각선 제외 모든 원소가 0

\(\begin{bmatrix} 4 &\ 0 &\ 0 \\ 0 &\ 5 &\ 0 \\ 0 &\ 0 &\ 6 \end{bmatrix}\)

NumPy’s diag 함수를 사용해서 대각행렬을 생성할 수 있다.

In [24]:np.diag([4, 5, 6])
Out[24]:array([[4, 0, 0],
                [0, 5, 0],
                [0, 0, 6]])

diag 함수에 행렬을 전달하면 주대각선 값들을 얻을 수 있다.
In [25]:D = np.array([
                [1, 2, 3],
                [4, 5, 6],
                [7, 8, 9],
        ])
        np.diag(D)
Out[25]:array([1, 5, 9])

단위행렬(identity matrix): 대각행렬이며 주대각선 원소들이 모두 1. \(I\)로 표시한다.

\[\begin{bmatrix} 1 &\ 0 &\ 0 \\ 0 &\ 1 &\ 0 \\ 0 &\ 0 &\ 1 \end{bmatrix}\]

Numpy의 eye 함수를 사용하면 원하는 크기의 단위행렬을 생성할 수 있다.

In [26]:np.eye(3)
Out[26]:array([[1., 0., 0.],
                [0., 1., 0.],
                [0., 0., 1.]])

전치 (Transpose)

행렬을 전치하는 것은 그 행렬을 뒤집는 것으로 생각할 수 있다. 행렬 \(A\in \mathbb{R}^{m\times n}\)이 주어졌을 때 그것의 전치행렬은 \(A^T \in \mathbb{R}^{n\times m}\)으로 표시하고 각 원소는 다음과 같이 주어진다.

\[\left( A^T \right)_{ij} = A_{ji}\]

다음의 성질들이 성립한다.

• \(A^T)^T = A\)
• \(\left(AB\right)^T = B^TA^T\)
• \((A + B)^T = A^T + B^T\)

\[A^T = \begin{bmatrix} 1 &\ 2 &\ 3 \\ 4 &\ 5 &\ 6 \end{bmatrix}^T = \begin{bmatrix} 1 &\ 4 \\ 2 &\ 5 \\ 3 &\ 6 \end{bmatrix}\]

Numpy의 T 속성(attribute)을 사용해서 전치행렬을 구할 수 있다.

In [27]:A = np.array([
                [1,2,3],
                [4,5,6]
                ])

In [28]:A.T
Out[28]:array([[1, 4],
                [2, 5],
                [3, 6]])

In [29]:A.T.T
Out[29]:array([[1, 2, 3],
                [4, 5, 6]])

In [30]:B = np.array([[1,2], [4, 5], [6, 7]])

In [31]:np.matmul(A, B).T
Out[31]:array([[27, 60],
                [33, 75]])

In [32]:np.matmul(B.T, A.T)
Out[32]:array([[27, 60],
                [33, 75]])

In [33]:B = np.array([[1,2,3], [4, 5, 6]])

In [34]:(A + B).T
Out[34]:array([[ 2,  8],
                [ 4, 10],
                [ 6, 12]])

In [35]:A.T + B.T
Out[35]:array([[ 2,  8],
                [ 4, 10],
                [ 6, 12]])

대칭행렬 (Symmetic Matrices)

정방행렬 \(A\)가 \(A^T\)와 동일할 때 대칭행렬이라고 부른다. \(A = -A^T\)일 때는 반대칭(anti-symmetric)행렬이라고 부른다.

\(AA^T\)는 항상 대칭행렬이다.

\(A + A^T\)는 대칭, \(A - A^T\)는 반대칭이다.
\(A = \frac{1}{2}(A+A^T)+\frac{1}{2}(A-A^T)\)

In [36]:np.matmul(A, A.T)
Out[36]:array([[14, 32],
                [32, 77]])

In [37]:np.matmul(A.T, A)
Out[37]:array([[17, 22, 27],
                [22, 29, 36],
                [27, 36, 45]])

대각합 (Trace)

정방행렬 \(A\in \mathbb{R}^{n\times n}\)의 대각합은 \(\mathrm{tr}(A)\)로 표시(또는 \(\mathrm{tr}A\))하고 그 값은 \(\sum_{i=1}^n A_{ii}\)이다. 대각합은 다음과 같은 성질을 가진다.

For \(A\in \mathbb{R}^{n\times n}\), \(\mathrm{tr}A = \mathrm{tr}A^T\) For \(A,B\in \mathbb{R}^{n\times n}\), \(\mathrm{tr}(A+B) = \mathrm{tr}A + \mathrm{tr}B\) For \(A\in \mathbb{R}^{n\times n}, t\in\mathbb{R}\), \(\mathrm{tr}(tA) = t\,\mathrm{tr}A\) For \(A, B\) such that \(AB\) is square, \(\mathrm{tr}AB = \mathrm{tr}BA\) For \(A, B, C\) such that \(ABC\) is square, \(\mathrm{tr}ABC = \mathrm{tr}BCA = \mathrm{tr}CAB\), and so on for the product of more matrices

In [38]:A = np.array([
                [100, 200, 300],
                [ 10,  20,  30],
                [  1,   2,   3],
        ])
        np.trace(A)
Out[38]:123

Norms

벡터의 norm은 벡터의 길이로 이해할 수 있다. \(l_2\) norm (Euclidean norm)은 다음과 같이 정의된다.

\[\left \Vert x \right \|_2 = \sqrt{\sum_{i=1}^n{x_i}^2}\]

\(\left \Vert x \right \|_2^2 = x^Tx\)임을 기억하라.

In [39]:import numpy.linalg as LA
        LA.norm(np.array([3, 4]))
Out[39]:5.0

\(l_p\) norm

\[\left \Vert x \right \|_p = \left(\sum_{i=1}^n|{x_i}|^p\right)^{1/p}\]

Frobenius norm (행렬에 대해서)

\[\left \Vert A \right \|_F = \sqrt{\sum_{i=1}^m\sum_{j=1}^n A_{ij}^2} = \sqrt{\mathrm{tr}(A^TA)}\]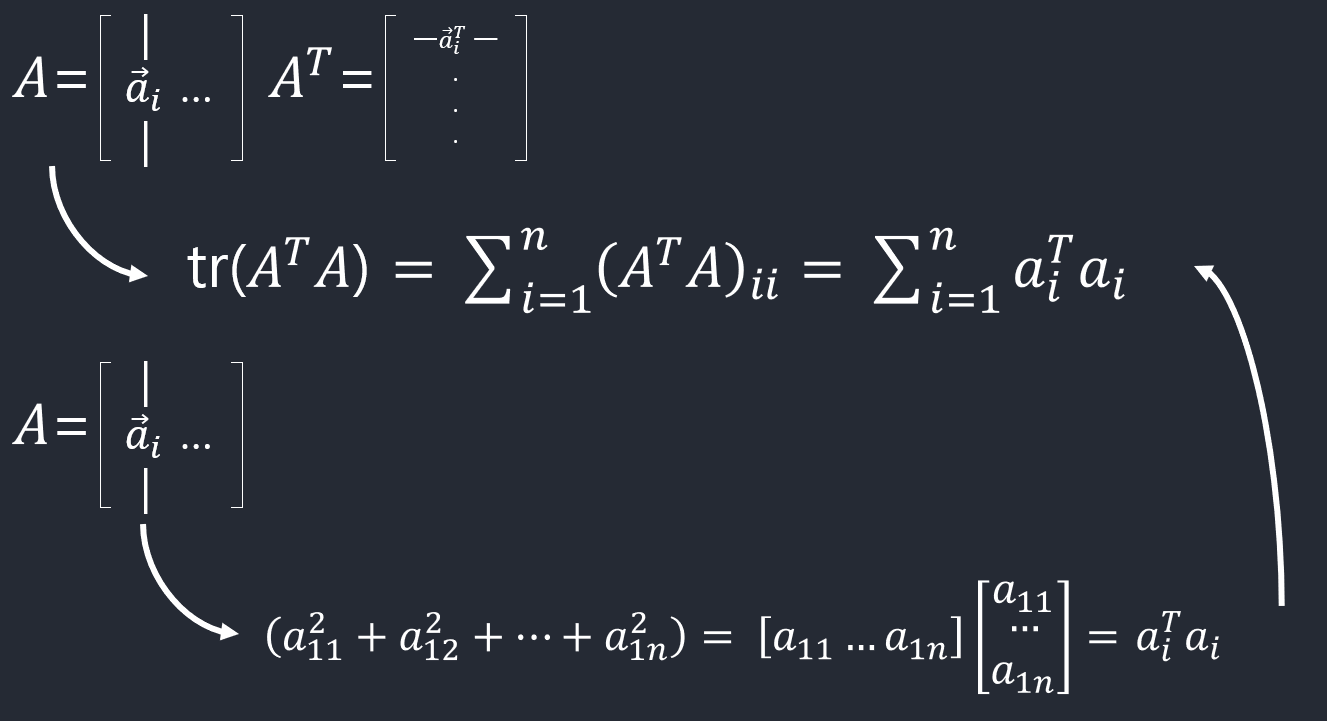

In [40]:A = np.array([
                [100, 200, 300],
                [ 10,  20,  30],
                [  1,   2,   3],
        ])

In [41]:LA.norm(A)
Out[41]:376.0505285197722

In [42]:np.trace(A.T.dot(A))**0.5
Out[42]:376.0505285197722

선형독립과 Rank (Linear Independence and Rank)

벡터들의 집합 \(\{x_1,x_2,\ldots,x_n\}\subset \mathbb{R}^m\)에 속해 있는 어떤 벡터도 나머지 벡터들의 선형조합으로 나타낼 수 없을 때 이 집합을 선형독립(linear independent)이라고 부른다. 역으로 어떠한 벡터가 나머지 벡터들의 선형조합으로 나타내질 수 있을 때 이 집합을 (선형)종속(dependent)이라고 부른다.

In [43]:A = np.array([
                [1, 4, 2],
                [2, 1, -3],
                [3, 5, -1],
        ])

위 행렬 \(A\)의 열들의 집합은 종속이다. 왜냐하면

In [44]:A[:, 2] == -2*A[:, 0] + A[:, 1]
Out[44]:array([ True,  True,  True])

행들의 집합도 마찬가지다.

첫 번째와 두 번째의 열벡터를 가지고 있는 집합은 선형독립이기 때문에 그 집합의 크기는 = 2, 따라서 Column rank = 2.
첫 번째와 두 번째의 행벡터를 가지고 있는 집합은 선형독립이기 때문에 그 집합의 크기는 = 2, 따라서 Row rank = 2.

Column rank: 행렬 \(A\in \mathbb{R}^{m\times n}\)의 열들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기

Row rank: 행렬 \(A\in \mathbb{R}^{m\times n}\)의 행들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기

모든 행렬의 column rank와 row rank는 동일하다. 따라서 단순히 \(\mathrm{rank}(A)\)로 표시한다. 다음의 성질들이 성립한다.

• For \(A\in \mathbb{R}^{m\times n}\), \(\mathrm{rank}(A) \leq \min(m, n)\). If \(\mathrm{rank}(A) = \min(m, n)\), then \(A\) is said to be full rank.
• For \(A\in \mathbb{R}^{m\times n}\), \(\mathrm{rank}(A) = \mathrm{rank}(A^T)\).
• For \(A\in \mathbb{R}^{m\times n}, B\in \mathbb{R}^{n\times p}\), \(\mathrm{rank}(A+B) \leq \min(\mathrm{rank}(A), \mathrm{rank}(B))\).
• For \(A, B\in \mathbb{R}^{m\times n}\), \(\mathrm{rank}(A+B) \leq \mathrm{rank}(A) + \mathrm{rank}(B)\).

\(\mathrm{rank}(A) = \mathrm{rank}(A^T)\):

\[\begin{align*} \mathrm{rank}(A^T) &= the\ number\ of\ pivot\ entries\ of\ rref(A)\ (reduced\ row\ echelron\ form).\\\\ \mathrm{rank}(A) &= dim(C(A)) = the\ number\ of\ vectors\ in\ the\ basis\ for\ C(A).\\\\ C(A) &= span(\overrightarrow{c_{1}},\overrightarrow{c_{2}},...,\overrightarrow{c_{n}})\\\\ \mathrm{rank}(A) &= the\ number\ of\ pivot\ entries\ of\ rref(A)\\\\ \end{align*}\]

Thus, \(\mathrm{rank}(A) = \mathrm{rank}(A^T)\)

\(rref(A)\): reduced row echelron form of matrix A

In [45]:LA.matrix_rank(A)
Out[45]:2

역행렬 (The Inverse)

정방행렬 \(A\in \mathbb{R}^{n\times n}\)의 역행렬 \(A^{-1}\)은 다음을 만족하는 정방행렬(\(\in \mathbb{R}^{n\times n}\))이다. \(A^{-1}A = I = AA^{-1}\)

\(A\)의 역행렬이 존재할 때, \(A\)를 invertible 또는 non-singular하다고 말한다.

\(A\)의 역행렬이 존재하기 위해선 \(A\)는 full rank여야 한다.

• \((A^{-1})^{-1} = A\)
• \((AB)^{-1} = B^{-1}A^{-1}\)
• \((A^{-1})^T = (A^T)^{-1}\)

In [46]:A = np.array([
                [1, 2],
                [3, 4],
        ])
        LA.inv(A)
Out[46]:array([[-2. ,  1. ],
                [ 1.5, -0.5]])

In [47]:LA.inv(LA.inv(A))
Out[47]:array([[1., 2.],
                [3., 4.]])

직교 행렬 (Orthogonal Matrices)

\(x^Ty=0\)가 성립하는 두 벡터 \(x, y \in \mathbb{R}^n\)를 직교(orthogonal)라고 부른다. \(\|x\|_2 = 1\)인 벡터 \(x\in \mathbb{R}^n\)를 정규화(normalized)된 벡터라고 부른다.

모든 열들이 서로 직교이고 정규화된 정방행렬 \(U\in \mathbb{R}^{n\times n}\)를 직교행렬이라고 부른다. 따라서 다음이 성립한다.

• \(U^TU = I\)
• \(UU^T = I\) 이건 밑에서 증명
• \(U^{-1} = U^T\)
• \(|Ux|_2 = |x|_2\) for any \(x\in \mathbb{R}^{n}\)

\(U^TU = I\):

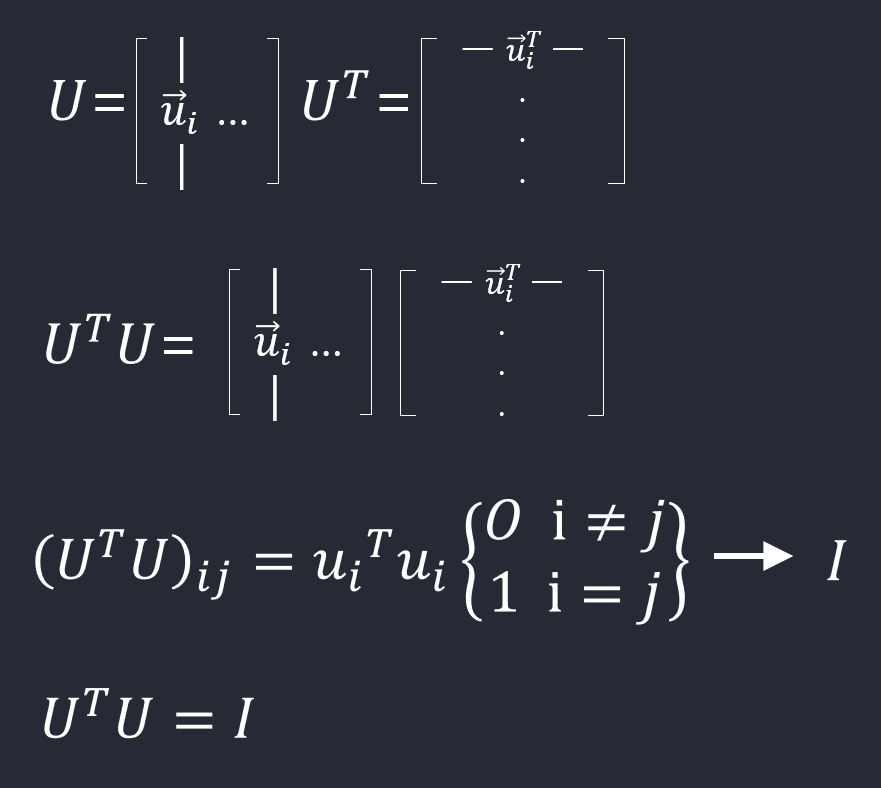
\(\|Ux\|_2 = \|x\|_2 for any x\in \mathbb{R}^{n}\):
U에 벡터x를 곱한 후 l2 norm 계산

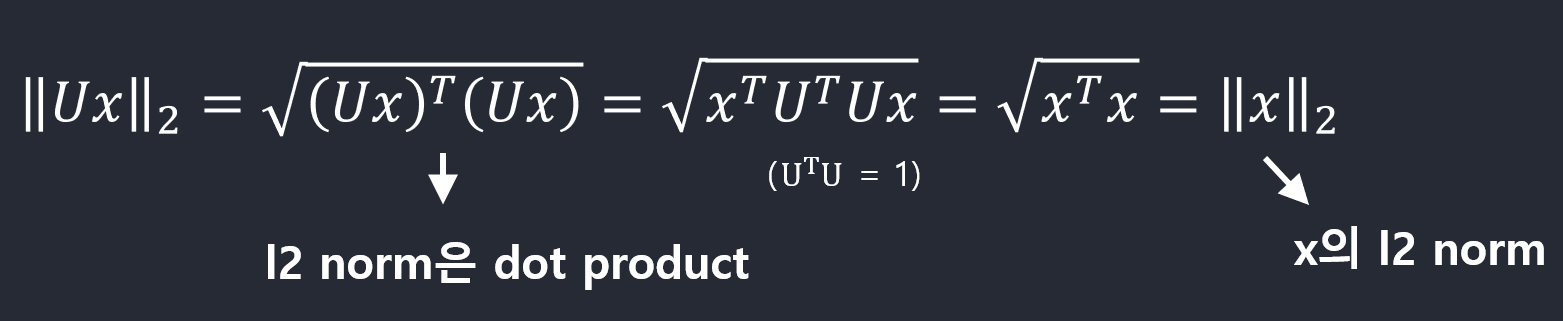
치역(Range), 영공간(Nullspace)

벡터의 집합(\(\{x_1,x_2,\ldots,x_n\}\))에 대한 생성(span)

\(\mathrm{span}(\{x_1,x_2,\ldots,x_n\}) = \left\{ v : v = \sum_{i=1}^n\alpha_i x_i, \alpha_i \in \mathbb{R} \right\}\)

행렬의 치역 (range)

행렬 \(A\in \mathbb{R}^{m\times n}\)의 치역 \(\mathcal{R}(A)\)는 A의 모든 열들에 대한 생성(span)이다. \(\mathcal{R}(A) = \{ v\in \mathbb{R}^m : v = Ax, x\in \mathbb{R}^n\}\)

영공간 (nullspace)

행렬 \(A\in \mathbb{R}^{m\times n}\)의 영공간(nullspace) \(\mathcal{N}(A)\)는 \(A\)와 곱해졌을 때 0이 되는 모든 벡터들의 집합이다. \(\mathcal{N}(A) = \{x\in \mathbb{R}^n : Ax = 0\}\)

치역은 차원이 m인 벡터들의 집합이고 영공간은 차원이 n인 벡터들의 집합이다. 이 두개의 차원이 다르다. 그런데 \(A^{T}\)의 치역(\(\mathcal{R}(A^T)\))과 A의 영공간(\(\mathcal{N}(A)\))은 같은 차원이다.

중요한 성질:

\(\{w : w = u + v, u\in \mathcal{R}(A^T), v \in \mathcal{N}(A)\} = \mathbb{R}^n ~\mathrm{and}~ \mathcal{R}(A^T) \cap \mathcal{N}(A) = \{0\}\)

• 전체공간(\(\mathbb{R}^n\))에서 임의의 점을 하나 선택을 하면 그 점을 \(\mathcal{R}(A^T)\)과 \(\mathcal{N}(A)\)에 속하는 두 개의 원소의 합(\(u + v\))으로 나타낼 수 있다.
• 임의의 점을 이런식으로 decompose할 수 있다는 점이다.
• \(\mathcal{R}(A^T) \cap \mathcal{N}(A)\) 하면 \(\mathbb{R}^{n}\)이라는 전체 공간이 만들어 진다.

\(\mathcal{R}(A^T)\)와 \(\mathcal{N}(A)\)를 직교여공간(orthogonal complements)라고 부르고 \(\mathcal{R}(A^T) = \mathcal{N}(A)^\perp\)라고 표시한다.

투영 (projection)

\(\mathcal{R}(A)\)위로 벡터 \(y\in \mathbb{R}^m\)의 투영(projection)은

\[\mathrm{Proj}(y;A) = \mathop{\mathrm{argmin}}_{v\in \mathcal{R}(A)} \| v - y \|_2 = A(A^TA)^{-1}A^Ty\]

\(U^TU = I\)인 정방행렬 \(U\)는 \(UU^T = I\)임을 보이기

\(U\)의 치역은 전체공간이므로 임의의 \(y\)에 대해 \(\mathrm{Proj}(y;U) = y\) 이어야 한다.
모든 \(y\)에 대해 \(U(U^TU)^{-1}Uy = y\) 이어야 하므로 \(U(U^TU)^{-1}U^T= I\) 이다.
따라서 \(UU^T = I\)이다.

행렬식 (Determinant)

정방행렬 \(A\in \mathbb{R}^{n\times n}\)의 행렬식(determinant) $$

A

\((또는\)\det A$$)는 다음과 같이 계산할 수 있다.

\[|A| = A_{1,1}\times|A^{(1,1)}| - A_{1,2}\times|A^{(1,2)}| + A_{1,3}\times|A^{(1,3)}| - A_{1,4}\times|A^{(1,4)}| + \cdots ± A_{1,n}\times|A^{(1,n)}|\]

where \(A^{(i,j)}\) is the matrix \(A\) without row \(i\) and column \(j\).

\[A = \begin{bmatrix} 1 &\ 2 &\ 3 \\ 4 &\ 5 &\ 6 \\ 7 &\ 8 &\ 0 \end{bmatrix}\]

위의 식을 사용하면 아래와 같이 전개된다. \(\begin{align*} |A| = 1 \times \left | \begin{bmatrix} 5 &\ 6 \\ 8 &\ 0 \end{bmatrix} \right | - 2 \times \left | \begin{bmatrix} 4 &\ 6 \\ 7 &\ 0 \end{bmatrix} \right | + 3 \times \left | \begin{bmatrix} 4 &\ 5 \\ 7 &\ 8 \end{bmatrix} \right | \end{align*}\)

이제 위의 \(2 \times 2\) 행렬들의 행렬식을 계산하면 된다.

\[\left | \begin{bmatrix} 5 &\ 6 \\ 8 &\ 0 \end{bmatrix} \right | = 5 \times 0 - 6 \times 8 = -48\] \[\left | \begin{bmatrix} 4 &\ 6 \\ 7 &\ 0 \end{bmatrix} \right | = 4 \times 0 - 6 \times 7 = -42\] \[\left | \begin{bmatrix} 4 &\ 5 \\ 7 &\ 8 \end{bmatrix} \right | = 4 \times 8 - 5 \times 7 = -3\]

최종결과는 다음과 같다.

\[|A| = 1 \times (-48) - 2 \times (-42) + 3 \times (-3) = 27\]

numpy.linalg 모듈의 det 함수를 사용하여 행렬식을 쉽게 구할 수 있다.

In [48]:A = np.array([
                [1, 2, 3],
                [4, 5, 6],
                [7, 8, 0]
        ])
        LA.det(A)
Out[48]:27.0

행렬식의 기하학적 해석

행렬 \(\begin{align*} \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_n^T & - \end{bmatrix} \end{align*}\) 이 주어졌을 때,

행 벡터들의 선형조합(단 조합에 쓰이는 계수들은 0에서 1사이)이 나타내는 \(\mathbb{R}^n\) 공간 상의 모든 점들의 집합 \(S\)를 생각해보자. 엄밀하게 나타내자면

\[S = \{v\in \mathbb{R}^n : v=\sum_{i=1}^n \alpha_i a_i ~\mathrm{where}~ 0\leq \alpha_i \leq 1, i=1,\ldots,n\}\]

중요한 사실은 행렬식의 절대값이 이 \(S\)의 부피(volume)과 일치한다는 것이다!

예를 들어, 행렬

\[A = \begin{bmatrix} 1 &\ 3 \\ 3 &\ 2 \end{bmatrix}\]

의 행벡터들은 \(a_1 = \begin{bmatrix} 1\\ 3 \end{bmatrix} a_2 = \begin{bmatrix} 3\\ 2 \end{bmatrix}\) 이다. \(S\)에 속한 점들을 2차원평면에 나타내면 다음과 같다.

평행사변형 \(S\)의 넓이는 7인데 이 값은 \(A\)의 행렬식 $$

A

=-7$$의 절대값과 일치함을 알 수 있다.

행렬식의 중요한 성질들

• \(\vert I\vert=1\)
• \(A\)의 하나의 행에 \(t\in \mathbb{R}\)를 곱하면 행렬식은 \(t\vert A\vert\)

\[\begin{align*} \left|~\begin{bmatrix} - & ta_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_n^T & - \end{bmatrix}~\right| = t|A| \end{align*}\]

• \(A\)의 두 행들을 교환하면 행렬식은 \(-\vert A\vert\)

\[\begin{align*} \left|~\begin{bmatrix} - & a_2^T & -\\ - & a_1^T & -\\ & \vdots &\\ - & a_n^T & - \end{bmatrix}~\right| = -|A| \end{align*}\]

• For \(A\in \mathbb{R}^{n\times n}, \vert A\vert = \vert A^T\vert\).
• For \(A, B\in \mathbb{R}^{n\times n}, \vert AB\vert = \vert A\vert \vert B\vert\).
• For \(A\in \mathbb{R}^{n\times n}, \vert A\vert=0\), if and only if A is singular (non-invertible). \(A\)가 singular이면 행들이 linearly dependent할 것인데, 이 경우 \(S\)의 형태는 부피가 0인 납작한 판의 형태가 될 것이다.
• For \(A\in \mathbb{R}^{n\times n}\) and \(A\) non-singular, \(\vert A^{-1}\vert = \frac{1}{\vert A\vert}\).

이차형식 (Quadratic Forms)

정방행렬 \(A\in \mathbb{R}^{n\times n}\)와 벡터 \(x\in \mathbb{R}^n\)가 주어졌을 때, scalar값 \(x^TAx\)를 이차형식(quadratic form)이라고 부른다. 다음과 같이 표현할 수 있다.

\[x^TAx = \sum_{i=1}^n x_i(Ax)_i = \sum_{i=1}^n x_i \left(\sum_{j=1}^n A_{ij}x_j\right) = \sum_{i=1}^n\sum_{j=1}^n A_{ij}x_ix_j\]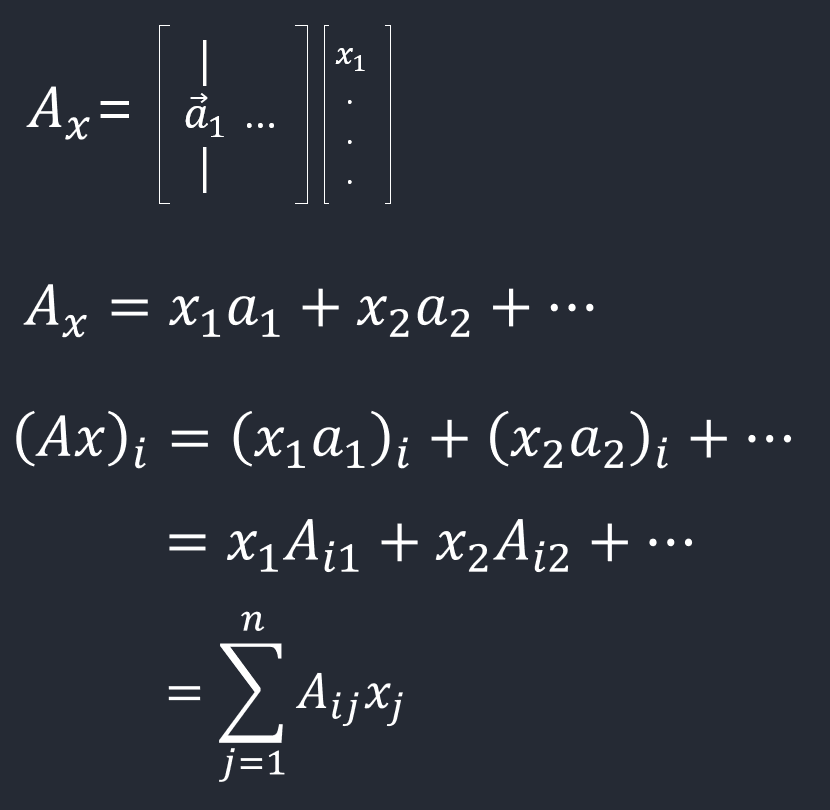

다음이 성립함을 알 수 있다.

\[x^TAx = (x^TAx)^T = x^TA^Tx = x^T\left(\frac{1}{2}A + \frac{1}{2}A^T\right)x\]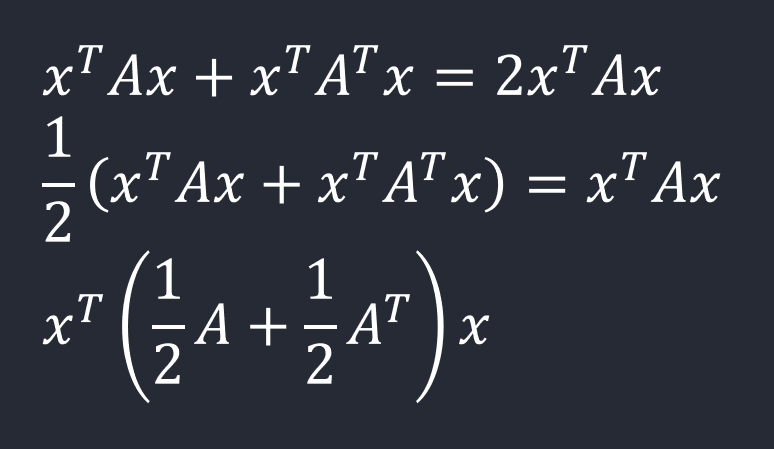

\(A+A^{T}\)인 행렬은 symmetric이다. 임의의 행렬 A가 주어졌을 때 이차형식의 값은 그 행렬 A의 symmetric한 부분에 의존한다는 점.

따라서 이차형식에 나타나는 행렬을 대칭행렬로 가정하는 경우가 많다.

• 대칭행렬 \(A\in \mathbb{S}^n\)이 0이 아닌 모든 벡터 \(x\in \mathbb{R}^n\)에 대해서 \(x^TAx \gt 0\)을 만족할 때, 양의 정부호(positive definite)라고 부르고 \(A\succ 0\)(또는 단순히 \(A \gt 0\))로 표시한다. 모든 양의 정부호 행렬들의 집합을 \(\mathbb{S}_{++}^n\)으로 표시한다.
• 대칭행렬 \(A\in \mathbb{S}^n\)이 0이 아닌 모든 벡터 \(x\in \mathbb{R}^n\)에 대해서 \(x^TAx \ge 0\)을 만족할 때, 양의 준정부호(positive sesmi-definite)라고 부르고 \(A\succeq 0\)(또는 단순히 \(A \ge 0\))로 표시한다. 모든 양의 준정부호 행렬들의 집합을 \(\mathbb{S}_{+}^n\)으로 표시한다.
• 대칭행렬 \(A\in \mathbb{S}^n\)이 0이 아닌 모든 벡터 \(x\in \mathbb{R}^n\)에 대해서 \(x^TAx \lt 0\)을 만족할 때, 음의 정부호(negative definite)라고 부르고 \(A\prec 0\)(또는 단순히 \(A \lt 0\))로 표시한다.
• 대칭행렬 \(A\in \mathbb{S}^n\)이 0이 아닌 모든 벡터 \(x\in \mathbb{R}^n\)에 대해서 \(x^TAx \leq 0\)을 만족할 때, 음의 준정부호(negative sesmi-definite)라고 부르고 \(A\preceq 0\)(또는 단순히 \(A \leq 0\))로 표시한다.
• 대칭행렬 \(A\in \mathbb{S}^n\)가 양의 준정부호 또는 음의 준정부호도 아닌 경우, 부정부호(indefinite)라고 부른다. 이것은 \(x_{1}^{T}Ax_{1} > 0, x_2^TAx_2 < 0\)을 만족하는 \(x_1, x_2\in \mathbb{R}^n\)이 존재한다는 것을 의미한다.

Positive definite 그리고 negative definite 행렬은 full rank이며 따라서 invertible이다.

Gram matrix

임의의 행렬 \(A\in \mathbb{R}^{m\times n}\)이 주어졌을 때 행렬 \(G = A^TA\)를 Gram matrix라고 부르고 항상 positive semi-definite이다. 만약 \(m\ge n\)이고 \(A\)가 full rank이면, \(G\)는 positive definite이다.

고유값 (Eigenvalues), 고유벡터 (Eigenvectors)

정방행렬 \(A\in \mathbb{R}^{n\times n}\)이 주어졌을 때,

\[Ax = \lambda x, x\neq 0\]

을 만족하는 \(\lambda \in \mathbb{C}\)를 \(A\)의 고유값(eigenvalue) 그리고 \(x\in \mathbb{C}^n\)을 연관된 고유벡터(eigenvector)라고 부른다.

Eigenvectors: 선형변환(T)이 일어난 후에도 방향이 변하지 않는 영벡터가 아닌 벡터.

Eigenvalues: Eigenvectors의 길이가 변하는 배수(scale), reversed나 scaled가 될 수 있지만 방향은 변하지 않는다.
They make for interesting basis vectors. Basis vectors whos transformation matrices are maybe computationally more simpler or ones that make for better coordinate systems.

numpy.linalg 모듈의 eig 함수를 사용하여 고유값과 고유벡터를 구할 수 있다.

In [49]:A
Out[49]:array([[1, 2, 3],
                [4, 5, 6],
                [7, 8, 0]])

In [50]:eigenvalues, eigenvectors = LA.eig(A)
        eigenvalues, eigenvectors
Out[50]:(array([12.12289378, -0.38838384, -5.73450994]),
        array([[-0.29982463, -0.74706733, -0.27625411],
                [-0.70747178,  0.65820192, -0.38842554],
                [-0.63999131, -0.09306254,  0.87909571]]))

In [51]:eigenvectors[:, 0]
Out[51]:array([-0.29982463, -0.70747178, -0.63999131])

In [52]:np.matmul(A, eigenvectors[:, 0])
Out[52]:array([-3.63474211, -8.57660525, -7.75854663])

In [53]:eigenvalues[0] * eigenvectors[:, 0]
Out[53]:array([-3.63474211, -8.57660525, -7.75854663])

고유값, 고유벡터의 성질들

• \(\mathrm{tr}A = \sum_{i=1}^n \lambda_i\).

• $$

  A

  = \prod_{i=1}^n \lambda_i$$.

• \(\mathrm{rank}(A)\)는 0이 아닌 \(A\)의 고유값의 개수와 같다.
• \(A\)가 non-singular일 때, \(1/\lambda_i\)는 \(A^{-1}\)의 고유값이다(고유벡터 \(x_i\)와 연관된). 즉, \(A^{-1}x_i = (1/\lambda_i)x_i\)이다. 대각행렬 \(D = \mathrm{diag}(d_1,\ldots,d_n)\)의 고유값들은 \(d_1,\ldots,d_n\)이다.

In [54]:A = np.array([
                [1, 2, 3],
                [4, 5, 9],
                [7, 8, 15]
        ])

In [55]:eigenvalues, eigenvectors = LA.eig(A)
        eigenvalues, eigenvectors
Out[55]:(array([ 2.12819293e+01, -2.81929326e-01,  9.68995205e-16]),
        array([[ 0.17485683,  0.85386809, -0.57735027],
                [ 0.50887555,  0.18337571, -0.57735027],
                [ 0.84289427, -0.48711666,  0.57735027]]))

In [56]:LA.matrix_rank(A)
Out[56]:2

모든 고유값과 고유벡터들을 다음과 같이 하나의 식으로 나타낼 수 있다.

\[AX = X\Lambda\] \[X\in \mathbb{R}^{n\times n} = \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ x_1 &\ x_2 &\ \cdots &\ x_n\\ \vert &\ \vert &\ &\ \vert \end{bmatrix},~ \Lambda = \mathrm{diag}(\lambda_1,\ldots,\lambda_n)\]

고유값, 고유벡터와 대칭행렬

대칭행렬 \(A\in \mathbb{S}^n\)가 가지는 놀라운 성질들

• \(A\)의 모든 고유값들은 실수값(real)이다.
• \(A\)의 고유벡터들은 orthonomal(orthogonal, normalized)이다.

따라서 임의의 대칭행렬 \(A\)를 \(A=U\Lambda U^T\)(\(U\)는 위의 \(X\)처럼 \(A\)의 고유벡터들로 이뤄진 행렬)로 나타낼 수 있다.

\(A\in \mathbb{S}^n = U\Lambda U^T\)라고 하자. 그러면

\[x^TAx = x^T U\Lambda U^T x = y^T\Lambda y = \sum_{i=1}^n \lambda_i y_i^2\]

where \(y=U^Tx\)

\(y_i^2\)가 양수이므로 위 식의 부호는 \(\lambda_i\) 값들에 의해서 결정된다. 만약 모든 \(\lambda_i > 0\)이면, \(A\)는 positive definite이고 모든 \(\lambda_i \ge 0\)이면, \(A\)는 positive seimi-definite이다.

행렬미분 (Matrix Calculus)

The Gradient

행렬 \(A\in \mathbb{R}^{m\times n}\)를 입력으로 받아서 실수값을 돌려주는 함수 \(f : \mathbb{R}^{m\times n} \to \mathbb{R}\)이 있다고 하자. \(f\)의 gradient는 다음과 같이 정의된다.

\[\nabla_Af(A)\in \mathbb{R}^{m\times n} = \begin{bmatrix} \frac{\partial f(A)}{\partial A_{11}} &\ \frac{\partial f(A)}{\partial A_{12}} &\ \cdots &\ \frac{\partial f(A)}{\partial A_{1n}}\\ \frac{\partial f(A)}{\partial A_{21}} &\ \frac{\partial f(A)}{\partial A_{22}} &\ \cdots &\ \frac{\partial f(A)}{\partial A_{2n}}\\ \vdots &\ \vdots &\ \ddots &\ \vdots\\ \frac{\partial f(A)}{\partial A_{m1}} &\ \frac{\partial f(A)}{\partial A_{m2}} &\ \cdots &\ \frac{\partial f(A)}{\partial A_{mn}} \end{bmatrix}\] \[(\nabla_Af(A))_{ij} = \frac{\partial f(A)}{\partial A_{ij}}\]

특별히 \(A\)가 벡터 \(x\in \mathbb{R}^n\)인 경우는,

\[\nabla_x f(x) = \begin{bmatrix} \frac{\partial f(x)}{\partial x_1}\\ \frac{\partial f(x)}{\partial x_2}\\ \vdots\\ \frac{\partial f(x)}{\partial x_n} \end{bmatrix}\]

The Hessian

\[\nabla_x^2 f(x)\in \mathbb{R}^{n\times n} = \begin{bmatrix} \frac{\partial^2 f(x)}{\partial x_1^2} &\ \frac{\partial^2 f(x)}{\partial x_1x_2} &\ \cdots &\ \frac{\partial^2 f(x)}{\partial x_1x_n}\\ \frac{\partial^2 f(x)}{\partial x_2x_1} &\ \frac{\partial^2 f(x)}{\partial x_2^2} &\ \cdots &\ \frac{\partial^2 f(x)}{\partial x_2x_n}\\ \vdots &\ \vdots &\ \ddots &\ \vdots\\ \frac{\partial^2 f(x)}{\partial x_nx_1} &\ \frac{\partial^2 f(x)}{\partial x_nx_2} &\ \cdots &\ \frac{\partial^2 f(x)}{\partial x_n^2} \end{bmatrix}\] \[(\nabla_x^2 f(x))_{ij} = \frac{\partial^2 f(x)}{\partial x_i \partial x_j}\]

중요한 공식들

\(x, b\in \mathbb{R}^n\), \(A\in \mathbb{S}^n\)일 때 다음이 성립한다.
x, b는 vector, A는 대칭행렬이라고 가정했을때,

• \(\nabla_x b^Tx = b\): \(b^T\)를 x에 대해서 gradient를 구한다.
• \(\nabla_x x^TAx = 2Ax\): 이차형식에서 x에 대해서 gradient를 구한다.
• \(\nabla_x^2 x^TAx = 2A\): \(2Ax\)를 다시 한번 x에 대해서 미분한다.
• \(\nabla_A \log \vert A\vert = A^{-1}(A\in\mathbb{S}_{++}^n)\)인 경우: 행렬 A에 대해서 gradient를 구한다. A의 행렬식을 A로 gradient를 구하게 되면

\(b^Tx\)대신에 \(bx\)에 대해서 미분한다고 하면, \((bx)^{'}=b\)가 된다.

이차형식 \(\nabla_x x^TAx = 2Ax\) 대신에, \((ax^2)'\) 에 대해서 미분하게 되면 \(2ax\)가 된다.

적용예제들

최소제곱법 (Least Squares)

행렬 \(A\in \mathbb{R}^{m\times n}\)(\(A\)는 full rank로 가정)와 벡터 \(b\in \mathbb{R}^n\)가 주어졌고 \(b\notin \mathcal{R}(A)\)인 경우, \(Ax = b\)를 만족하는 벡터 \(x\in \mathbb{R}^n\)을 찾을 수 없다. 대신 \(Ax\)가 \(b\)와 최대한 가까워지는 \(x\), 즉

\[\| Ax - b\|_2^2\]

을 최소화시키는 \(x\)를 찾는 문제를 고려할 수 있다. \(\|x\|_2^2 = x^Tx\)이므로

\[\begin{align*} \| Ax - b\|_2^2 &= (Ax - b)^T(Ax - b)\\ &= x^TA^TAx - 2b^TAx + b^Tb \end{align*}\]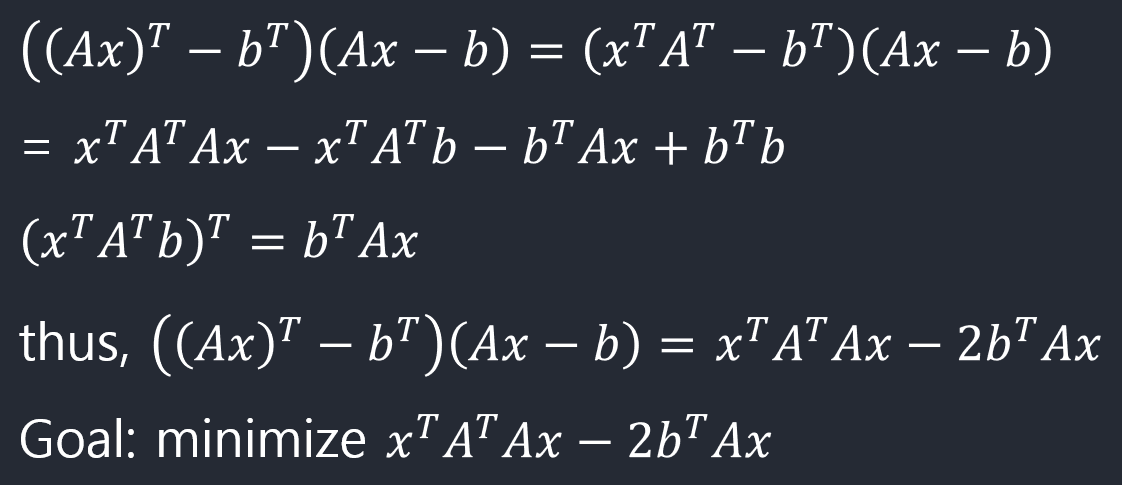

\(\begin{align*} \nabla_x (x^TA^TAx - 2b^TAx + b^Tb) &= \nabla_x x^TA^TAx - \nabla_x 2b^TAx + \nabla_x b^Tb\\ &= 2A^TAx - 2A^Tb \end{align*}\)
x에 관한 부분만 남겨놓기 때문에 \(b^Tb\)는 사라지고 \(2A^TAx - 2A^Tb\)만 남게 된다.
이차형식 부분인 \(\nabla_x x^TA^TAx\)을 미분하게 되면 위에서 나왔듯이, \(2A^TAx\)가 되고
\(\nabla_x 2b^TAx\) 이것도 역시 미분하게 되면 \(2A^Tb\)가 된다.

0으로 놓고 \(x\)에 관해 풀면 \(x = (A^TA)^{-1}A^Tb\)

고유값과 최적화문제 (Eigenvalues as Optimization)

다음 형태의 최적화문제를 행렬미분을 사용해 풀면 고유값이 최적해가 되는 것을 보일 수 있다.
\(\max_{x\in \mathbb{R}^n} x^TAx \mathrm{~~~~subject~to~} \|x\|_2^2=1\)

\(x^TAx\) 을 최대화 시키는 문제에서 제약조건이 \(\|x\|_2^2=1\) (x의 l2 norm이 1이다.)

제약조건이 있는 최소화문제는 Lagrangian을 사용해서 해결 \(\mathcal{L}(x, \lambda) = x^TAx - \lambda x^Tx\)

다음을 만족해야 함. \(\nabla_x \mathcal{L}(x, \lambda) = \nabla_x ( x^TAx - \lambda x^Tx) = 2A^Tx - 2\lambda x = 0\)

따라서 최적해 \(x\)는 \(Ax = \lambda x\)를 만족해야 하므로 \(A\)의 고유벡터만이 최적해가 될 수 있다. 고유벡터 \(u_i\)는
\(u_i^TAu_i = \sum_{j=1}^n \lambda_j y_j^2 = \lambda_i\)

을 만족하므로(\(y=U^Tu_i\)), 최적해는 가장 큰 고유값에 해당하는 고유벡터이다.

고유값, 고유벡터와 대칭행렬에서 나온
\(x^TAx = = \sum_{i=1}^n \lambda_i y_i^2\)
\(y=U^Tx\)인데 우리가 알아야할 것은 \(y_j\)의 값이다.

Autoencoder와 Principal Components Analysis (PCA)

Autoencoder란?

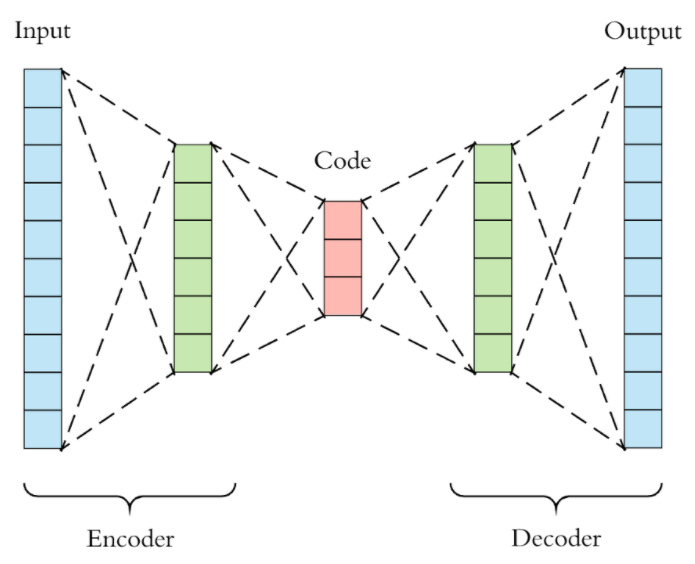
Autoencoder의 응용예제

• Dimensionality Reduction
• Image Compression
• Image Denoising
• Feature Extraction
• Image generation
• Sequence to sequence prediction
• Recommendation system

PCA를 가장 간단한 형태의 autoencoder로 생각할 수 있다. 이 관점으로 PCA를 유도할텐데, 이제까지 우리가 배운 것만으로 가능하다!

\(m\)개의 점들 \(\{x_1,\ldots,x_m\}\), \(x_i\in \mathbb{R}^n\)이 주어졌다고 하자. 각각의 점들을 \(l\)차원의 공간으로 투영시키는 함수 \(f(x) = c\in \mathbb{R}^l\)와 이것을 다시 \(n\)차원의 공간으로 회복하는 함수 \(g(c)\)를 생각해보자. \(f\)를 인코딩 함수, \(g\)를 디코딩 함수라고 부르며 \(x \approx g(f(x))\)

가 되기를 원한다. 디코딩 함수

함수 \(g\)는 간단한 선형함수로 정의하기로 한다. \(g(c) = Dc, ~~D\in \mathbb{R}^{n\times l}\)

여기서 \(D\)는 열들이 정규화되어 있고 서로 직교하는 경우로 한정한다. 인코딩 함수

디코딩 함수가 위와 같이 주어졌을 때, 어떤 함수가 최적의 인코딩 함수일까? \(f(x)^* = \mathop{\mathrm{argmin}}_{f(x)} \int \| x - g(f(x))\|_2^2 dx\)

변분법(calculus of variations)의 방법(Euler-Lagrange 방정식)으로 풀 수 있다. 방정식 \(\nabla_f \| x - g(f(x))\|_2^2 = 0\)

을 \(f\)에 관해 풀면 된다. \(f(x)=c\)로 두고 두면

\[\begin{align*} \| x - g(c)\|_2^2 &= (x-g(c))^T(x-g(c))\\ &= x^Tx - x^Tg(c) - g(c)^Tx + g(c)^Tg(c)\\ &= x^Tx - 2x^Tg(c) + g(c)^Tg(c)\\ &= x^Tx - 2x^TDc + c^TD^TDc\\ &= x^Tx - 2x^TDc + c^TI_lc\\ &= x^Tx - 2x^TDc + c^Tc\\ \end{align*}\]

\(\nabla_c (x^Tx - 2x^TDc + c^Tc) = 0\)
\(-2D^Tx + 2c = 0\)
\(c = D^Tx\)

따라서 최적의 인코더 함수는 \(f(x) = D^Tx\)
최적의 \(D\) 찾기

입력값 \(x\)와 출력값 \(g(f(x))\) 사이의 거리가 최소화되는 \(D\)를 찾는다.

\[\begin{align*} X = \begin{bmatrix} - & x_1^T & -\\ & \vdots &\\ - & x_m^T & - \end{bmatrix},~~ R = \begin{bmatrix} - & g(f(x_1))^T & -\\ & \vdots &\\ - & g(f(x_m))^T & - \end{bmatrix} \end{align*}\]

에러행렬 \(E\)를 다음과 정의할 수 있다.
\(E = X - R\)

우리가 찾는 최적의 \(D\)는 다음과 같다.
\(D^* = \mathop{\mathrm{argmin}}_{D} \|E\|_F^2~~~\mathrm{subject~to~} D^TD=I_l\)

\(R\)을 다시 정리해보자.

\[\begin{align*} R &= \begin{bmatrix} - & g(f(x_1))^T & -\\ & \vdots &\\ - & g(f(x_m))^T & - \end{bmatrix}\\ &= \begin{bmatrix} - & \left(DD^Tx_1 \right)^T & -\\ & \vdots &\\ - & \left(DD^Tx_m \right)^T & - \end{bmatrix}\\ &= \begin{bmatrix} - & x_1^TDD^T & -\\ & \vdots &\\ - & x_m^TDD^T & - \end{bmatrix}\\ &= XDD^T \end{align*}\] \[\begin{align*} \mathop{\mathrm{argmin}}_{D} \|E\|_F^2 &= \mathop{\mathrm{argmin}}_{D} \| X - XDD^T\|_F^2\\ &= \mathop{\mathrm{argmin}}_{D} \mathrm{tr}\left( \left(X - XDD^T\right)^T\left(X - XDD^T\right) \right)\\ &= \mathop{\mathrm{argmin}}_{D} \mathrm{tr} \left( X^TX - X^TXDD^T - DD^TX^TX + DD^TX^TXDD^T \right)\\ &= \mathop{\mathrm{argmin}}_{D} \mathrm{tr} \left( X^TX \right) - \mathrm{tr} \left( X^TXDD^T \right) - \mathrm{tr} \left( DD^TX^TX \right) + \mathrm{tr} \left( DD^TX^TXDD^T \right)\\ &= \mathop{\mathrm{argmin}}_{D} - \mathrm{tr} \left( X^TXDD^T \right) - \mathrm{tr} \left( DD^TX^TX \right) + \mathrm{tr} \left( DD^TX^TXDD^T \right)\\ &= \mathop{\mathrm{argmin}}_{D} - 2\mathrm{tr} \left( X^TXDD^T \right) + \mathrm{tr} \left( DD^TX^TXDD^T \right)\\ &= \mathop{\mathrm{argmin}}_{D} - 2\mathrm{tr} \left( X^TXDD^T \right) + \mathrm{tr} \left( X^TXDD^TDD^T \right)\\ &= \mathop{\mathrm{argmin}}_{D} - 2\mathrm{tr} \left( X^TXDD^T \right) + \mathrm{tr} \left( X^TXDD^T \right)\\ &= \mathop{\mathrm{argmin}}_{D} - \mathrm{tr} \left( X^TXDD^T \right)\\ &= \mathop{\mathrm{argmin}}_{D} - \mathrm{tr} \left( D^TX^TXD \right)\\ &= \mathop{\mathrm{argmax}}_{D} \mathrm{tr} \left( D^TX^TXD\right)\\ &= \mathop{\mathrm{argmax}}_{d_1,\ldots,d_l} \sum_{i=1}^l d_i^TX^TXd_i \end{align*}\]

\(d_i^Td_i = 1\)이므로 벡터들 \(d_1,\ldots,d_l\)이 \(X^TX\)의 가장 큰 \(l\)개의 고유값에 해당하는 고유벡터들일 때

\(\sum_{i=1}^l d_i^TX^TXd_i\)이 최대화된다.

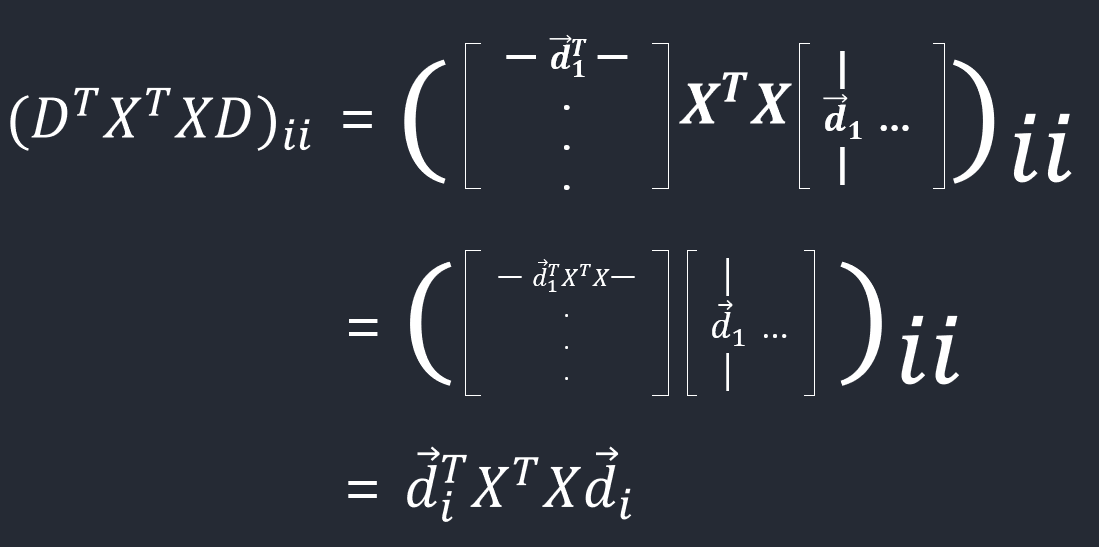
Appendix

Basis of a Subspace

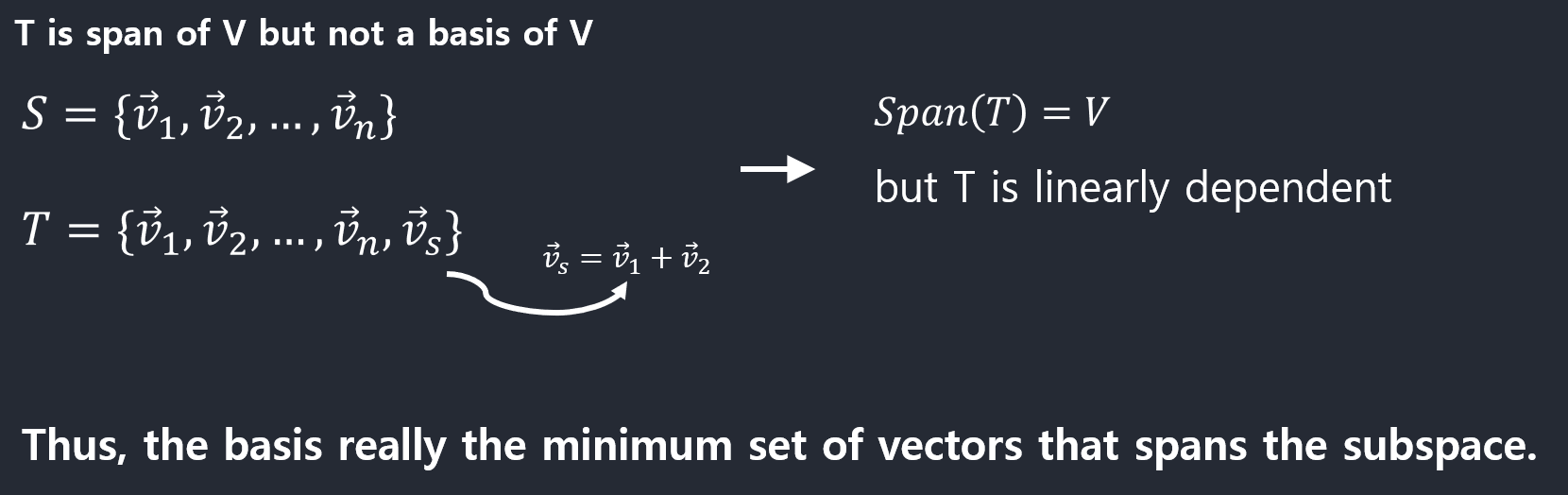
MathJax

\({\sim}A\)
\(\sim{A}\):

$${\sim}A$$
$$\sim A$$

align
\(\begin{align*} A = \begin{bmatrix} a_{11} &\ a_{12} &\ \cdots &\ a_{1n}\\ a_{21} &\ a_{22} &\ \cdots &\ a_{2n}\\ \vdots &\ \vdots &\ \ddots &\ \vdots\\ a_{m1} &\ a_{m2} &\ \cdots &\ a_{mn} \end{bmatrix} \end{align*}\)

\[\begin{align*} A = \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ a_1 &\ a_2 &\ \cdots &\ a_n\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} \end{align*}\]

\(\begin{align*} A = \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_m^T & - \end{bmatrix} \end{align*}\):

$$\begin{align*} A = \begin{bmatrix} a_{11} &\ a_{12} &\ \cdots &\ a_{1n}\\ a_{21} &\ a_{22} &\ \cdots &\ a_{2n}\\ \vdots &\ \vdots &\ \ddots &\ \vdots\\ a_{m1} &\ a_{m2} &\ \cdots &\ a_{mn} \end{bmatrix} \end{align*}$$  

$$\begin{align*} A = \begin{bmatrix} \vert &\ \vert &\ &\ \vert\\ a_1 &\ a_2 &\ \cdots &\ a_n\\ \vert &\ \vert &\ &\ \vert \end{bmatrix} \end{align*}$$  

$$\begin{align*} A = \begin{bmatrix} - & a_1^T & -\\ - & a_2^T & -\\ & \vdots &\\ - & a_m^T & - \end{bmatrix} \end{align*}$$  

\(\overrightarrow{c_{1}}\):

$$\overrightarrow{c_{1}}$$

mathjax as list

• \(U^TU = I\)
• \(U^{-1} = U^T\):

- \\(U^TU = I\\)
- \\(U^{-1} = U^T\\)

가변 괄호 with escape curly brackets \(\left\{-\frac{1}{2\sigma^{2}} \sum_{n=1}^{N}(x_{n}-\mu)^{2} \right\}\):

$$\left\{-\frac{1}{2\sigma^{2}} \sum_{n=1}^{N}(x_{n}-\mu)^{2} \right\}$$ 

References

Pattern Recognition and Machine Learning: https://tensorflowkorea.files.wordpress.com/2018/11/bishop-pattern-recognition-and-machine-learning-2006.pdf
rank(a) == rank(transpose A) : https://www.youtube.com/watch?v=tqqVOWm9YsU
eigenvalue, eigenvector: https://www.youtube.com/watch?v=PhfbEr2btGQ
basis of subspace: https://www.youtube.com/watch?v=zntNi3-ybfQ