Assignment - KNN

This assignment basically comes from cs231n. https://cs231n.github.io/assignments2021/assignment1/#q1-k-nearest-neighbor-classifier

KNN

Taking majority vote from K closest points instead of copying label from nearest neighbor.

Inline Question 1

Notice the structured patterns in the distance matrix, where some rows or columns are visible brighter. (Note that with the default color scheme black indicates low distances while white indicates high distances.)

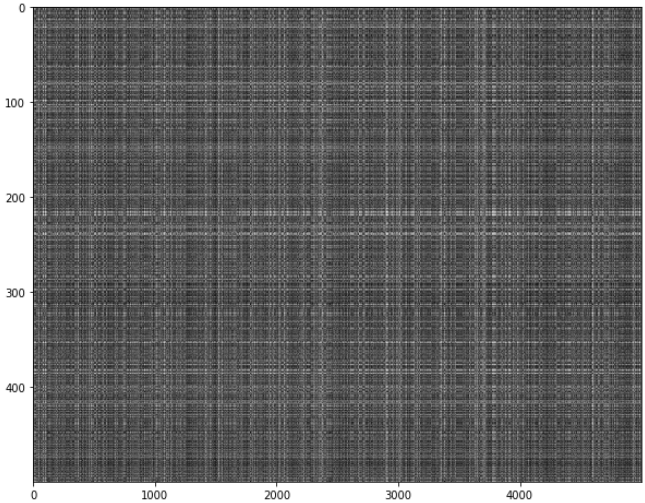
• What in the data is the cause behind the distinctly bright rows?
• What causes the columns?

Your Answer:

• Bright rows means that test samples of n-th row have further distance than others with train samples.
• It’s the row of train samples that shows further distance with test samples.

Inline Question 2

We can also use other distance metrics such as L1 distance.
For pixel values \(p_{ij}^{(k)}\) at location \((i,j)\) of some image \(I_k\),

the mean \(\mu\) across all pixels over all images is \(\mu=\frac{1}{nhw}\sum_{k=1}^n\sum_{i=1}^{h}\sum_{j=1}^{w}p_{ij}^{(k)}\)
And the pixel-wise mean \(\mu_{ij}\) across all images is \(\mu_{ij}=\frac{1}{n}\sum_{k=1}^np_{ij}^{(k)}.\)
The general standard deviation \(\sigma\) and pixel-wise standard deviation \(\sigma_{ij}\) is defined similarly.

Which of the following preprocessing steps will not change the performance of a Nearest Neighbor classifier that uses L1 distance? Select all that apply.

1. Subtracting the mean \(\mu\) (\(\tilde{p}_{ij}^{(k)}=p_{ij}^{(k)}-\mu\).)
2. Subtracting the per pixel mean \(\mu_{ij}\) (\(\tilde{p}_{ij}^{(k)}=p_{ij}^{(k)}-\mu_{ij}\).)
3. Subtracting the mean \(\mu\) and dividing by the standard deviation \(\sigma\).
4. Subtracting the pixel-wise mean \(\mu_{ij}\) and dividing by the pixel-wise standard deviation \(\sigma_{ij}\).
5. Rotating the coordinate axes of the data.

Your Answer

• 1,3

Your Explanation

• 1,3: the same \(\mu\) and \(\sigma\) will affect across all distance.
• 2,4: each pixel can have different \(\mu\) and \(\sigma\), and this will affect the L1 distance.
• 5: L1 is dependent on the coordinate and this will change the performance.

Why L1 is dependent to the coordinate axes of the data. (Explanation of 2-5)

L1 distance depends on your choice of coordinate system. So if you’re to rotate the coordinate frame that would actually change the L1 distance between two points.
Whereas changing the coordinate frame in the L2 distance doesn’t matter, it’s the same thing no matter what your coordinate frame is.

So, if your input features, if the individual entries in your vector have some important meaning for your task, then maybe somehow L1 might be a more natural fit. But, if it’s just a generic vector in some space and you don’t know which of the different elements, you don’t know what they actually mean, then maybe L2 is slightly more natural.

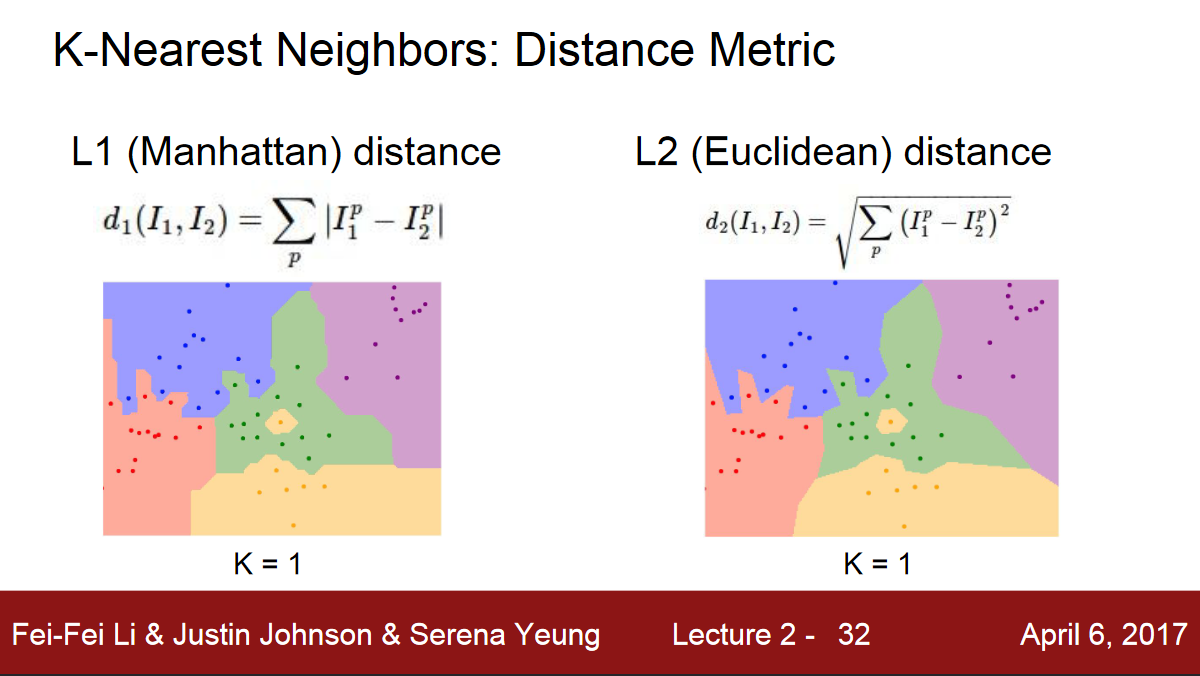
What is actually happening geometrically if we choose different distance metrics?

The shape of the decision boundaries actually change quite a bit between the two metrics.
Looking at L1, these decision boundaries tend to follow the coordinate axes.
Because L1 depends of our choice of coordinate system.

Where the L2 doesn’t really care about the coordinate axes. It just puts the boundaries where they should fall naturally.

Rotation of coordinate axes and L1

Consider three points \(x=(0,1),y=(1,0),z=(2,1)\).

Then

\[\begin{align*}\Vert y-x\Vert_1&=\Vert y-z\Vert_1\\&=2\end{align*}\]

so that \(x\) and \(z\) both have the same distance from \(y\). Now consider the 45 degree rotation matrix

\[\begin{align*}A&=\left(\begin{array}{cc}\frac{\sqrt{2}}{2}&-\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\end{array}\right)\end{align*}\] \[\begin{align*}x'&=Ax\\&=\left(\begin{array}{c}-\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}\end{array}\right)\\y'&=Ay\\&=\left(\begin{array}{c}\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}\end{array}\right)\\z'&=Az\\&=\left(\begin{array}{c}\frac{3\sqrt{2}}{2}\\\sqrt{2}\end{array}\right)\end{align*}\] \[\begin{align*}\Vert x'-y'\Vert_1&=2\sqrt{2}\\\Vert y'-z'\Vert_1&=\frac{5}{2}\sqrt{2}\end{align*}\]

and thus

\[\Vert x'-y'\Vert_1<\Vert y'-z'\Vert_1\]

L1 distance ordering is then not preserved under rotation.

Inline Question 3

Which of the following statements about \(k\)-Nearest Neighbor (\(k\)-NN) are true in a classification setting, and for all \(k\)? Select all that apply.

1. The decision boundary of the k-NN classifier is linear.
2. The training error of a 1-NN will always be lower than or equal to that of 5-NN.
3. The test error of a 1-NN will always be lower than that of a 5-NN.
4. The time needed to classify a test example with the k-NN classifier grows with the size of the training set.
5. None of the above.

Your Answer

• 2, 4

Your Explanation

• 1: False. The decision boundaries of kNN are locally linear segments, but in general have a complex shape that is not equivalent to a line in 2D or a hyperplane in higher dimensions.
• 2: True. If you use the training data set as the test set, then with one nearest neighbor, if given a point x, the nearest neighbor will be the exact same point and thus the error will be 0. For 5-NN, 0 is a lower bound.
• 3: False. Consider a 1d example. You have \(x_{\textrm{train}}=(-5,-4,-3,-2,-1,3)\) and \(y_{\textrm{train}}=(0,0,0,0,0,1)\). Now consider a new point with x=2 and y=0. Then this will have test error 100% for 1-nn and 0% for 5-nn.
• 4: True. KNN needs to calculate the whole data.

Appendix

Reference

Lecture 2 | Image Classification: https://youtu.be/OoUX-nOEjG0 slides: http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture2.pdf Rotate coordinate system and L1: https://boostedml.com/2018/12/solutions-to-stanfords-cs-231n-assignments-1-inline-problems-knn.html https://cs231n.github.io/classification/
https://cs231n.github.io/classification/#k---nearest-neighbor-classifier
https://nlp.stanford.edu/IR-book/html/htmledition/linear-versus-nonlinear-classifiers-1.html