ML basics - Decision Theory & Linear Regression

Deep Learning Model’s Outcome is the Probability of the Variable X

Decision Theory

새로운 값 \(\mathbf x\)가 주어졌을 때 확률모델 \(p(\mathbf x,\mathbf t)\)에 기반해 최적의 결정(ex. 분류)을 내리는 것.
추론단계: 결합확률분포 \(p(\mathbf x, C_{k})\)를 구하는 것 (\(p(C_{k}\mid\mathbf x)\)). 이것만 있으면 모든 것을 할 수 있음
결정단계: 상황에 대한 확률이 주어졌을 때 어떻게 최적의 결정을 내릴 것인지? 추론단계를 거쳤다면 결정단계는 매우 쉽다.

예제: X-Ray 이미지로 암 판별

• \(\mathbf x\): X-Ray 이미지
• \(C_{1}\): 암인 경우
• \(C_{2}\): 암이 아닌 경우
• \(p(C_{k}\mid\mathbf x)\)의 값을 알기 원함

\[\begin{align} p(C_{k}\mid\mathbf x) &= \frac{ p(\mathbf x, C_{k}) }{p(x)} \\\\ &= \frac{ p(\mathbf x, C_{k}) }{ \sum_{k=1}^{2}\ p(\mathbf x, C_{k}) } \\\\ &= \frac{ p(\mathbf x\mid C_{k})\ p(C_{k}) }{p(\mathbf x)} \\\\ &\propto Likelihood \times\ Prior \\\\ \end{align}\]

직관적으로 볼 때 \(p(C_{k}\mid\mathbf x)\)를 최대화 시키는 k를 구하는 것이 좋은 결정

Binary Classification

Decision Region

\(\mathcal{R}_{i} = \{x:pred(x) = C_{i}\}\)

\(x\)가 \(C_{i}\) 클래스로 할당을 하게 되면(혹은 분류를 하게 되면) \(x\)는 \(\mathcal{R}_{i}\)에 속하게 된다.
각각의 \(\mathcal{R}_{i}\)는 \(x\)의 집합이라고 볼 수 있다.
클래스 \(i\)에 속하는 모든 \(x\)의 집합.

Prob of Misclassification

\(\begin{align} p(mis) &= p(x \in \mathcal{R}_{1}, C_{2}) + p(x \in \mathcal{R}_{2}, C_{1}) \\\\ &= \int_{\mathcal{R}_{1}}\ p(x, C_{2})dx + \int_{\mathcal{R}_{2}}\ p(x, C_{1})dx \\\\ \end{align}\)

\(p(x \in \mathcal{R}_{1}, C_{2})\): class 1으로 분류를 했지만 실제로는 class 2인 확률
\(p(x \in \mathcal{R}_{2}, C_{1})\): class 2으로 분류를 했지만 실제로는 class 1인 확률

이것을 적분의 형태로 나태낸 것이 \(\int_{\mathcal{R}_{1}}\ p(x, C_{2})dx + \int_{\mathcal{R}_{2}}\ p(x, C_{1})dx\)

\(\int_{\mathcal{R}_{1}}\ p(x, C_{2})dx\)의 area는 그래프에서 빨간색과 초록색으로 칠해진 면적이다.
\(\int_{\mathcal{R}_{2}}\ p(x, C_{1})dx\)의 area는 그래프에서 보라색으로 칠해진 면적이다.

결국 분류오류 확률은 색이 칠해진 면적의 총합이라고 볼 수 있다.

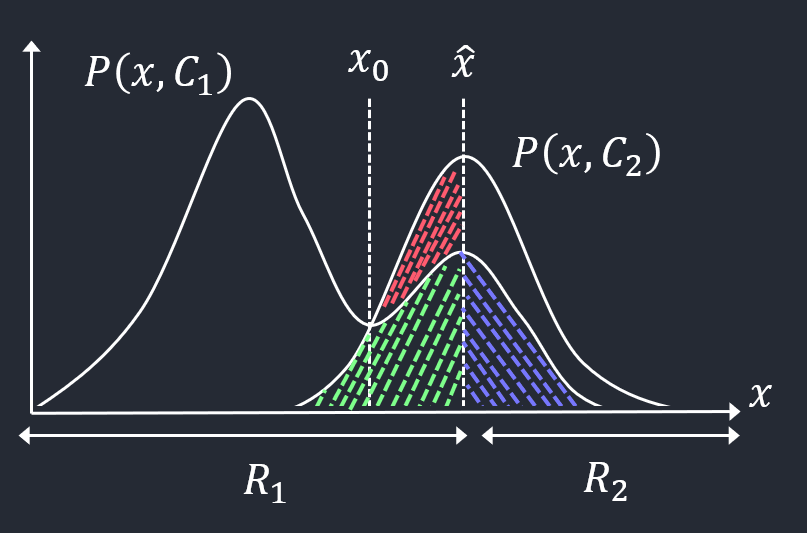
Minimize Misclassification

\(\hat x\)가 왼쪽으로 이동한다면,
에러를 만들어내는 부분에 있어서 변하는 영역과 변하지 않는 영역이 있다.
빨간색 영역은 \(\hat x\)이 왼쪽으로 이동함에 따라 줄어들었고, 나머지 영역들은 변하지 않는다.
빨간색 영역을 최소화시키면 전체 에러 영역이 최소화될 것이다.

\(\hat x\)이 \(x_{0}\)값을 가지는 영역에서는 빨간색 영역이 완전히 사라지고 최소화가 된다.

오류를 최소화하기위해 \(p(x, C_{1}) > p(x, C_{2})\)이 되면 \(x\)를 \(\mathcal{R}_{1}\)에 할당해야 한다.

\(p(x, C_{1}) < p(x, C_{2})\)이 되면 C1에 할당하는 것이 아니라 C2에 할당하게 되면 오류를 최소화 할 수 있다.

\[\begin{align} p(x, C_{1}) > p(x, C_{2}) &\Leftrightarrow p(C_{1}\mid x)p(x) > p(C_{2}\mid x)p(x) \\\\ &\Leftrightarrow p(C_{1}\mid x) > p(C_{2}\mid x) \\\\ \end{align}\]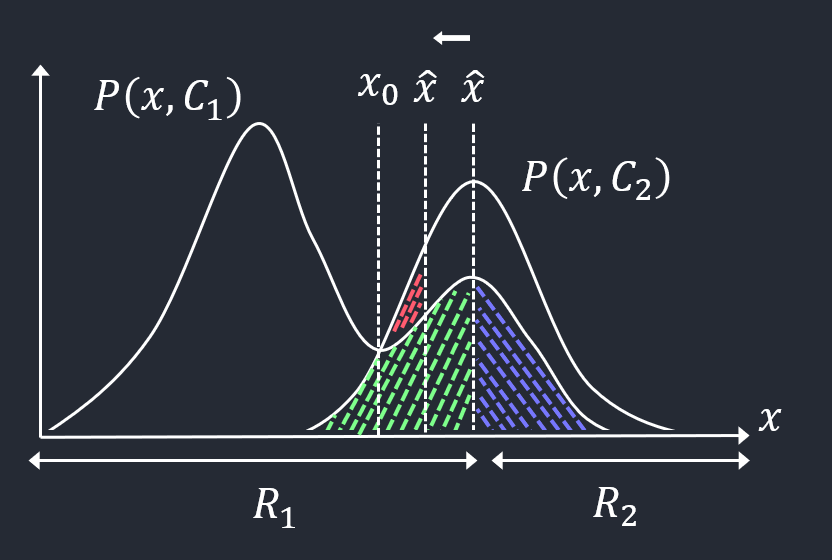

Multiclass

multiclass의 경우 오류보다 정확성에 초점을 맞추는 것이 좋다.

\[\begin{align} p(correct) &= \sum_{k=1}^{K}p(\mathbf x \in \mathcal{R_{k}}, \mathcal{C_{k}}) \\\\ &= \sum_{k=1}^{K}\int_{\mathcal{R_{k}}}p(\mathbf x, \mathcal{C_{k}})dx \\\\ \end{align}\] \[pred(x) = \arg\max_{k}p(C_{k}\mid x)\]

Objective of Decision Theory (Classification)

결합확률분포 \(p(\mathbf x, C_{k})\)가 주어졌을 때 최적의 결정영역들 \(\mathcal{R_{1}},...,\mathcal{R_{K}}\)를 찾는 것
\(\hat C(\mathbf x)\)를 \(\mathbf x\)가 주어졌을 때 예측값 \((1,...,K 중 하나의 값)\)을 돌려주는 함수라고 하자.

\[\mathbf x \in \mathcal{R_{i}} \Leftrightarrow \hat C(\mathbf x) = j\]

결합확률분포 \(p(\mathbf x, C_{k})\)가 주어졌을 때 최적의 함수 \(\hat C(\mathbf x)\)를 찾는 것.
‘최적의 함수’는 어떤 기준으로?

Minimizing the Expected Loss

앞에서 오류를 최소화 한다고 했지만 조금 더 확장한다면 기댓값으로 갈 수 있을 것이다.

모든 결정이 동일한 리스크를 갖는 것이 아님

• 암이 아닌데 암으로 진단
• 암인데 암이 아닌 것으로 진단 (risky)

손실행렬 (Loss Matrix)

• \(L_{kj}\): \(C_{k}\)에 속하는 \(\mathbf x\)를 \(C_{j}\)로 분류할 때 발생하는 손실
  

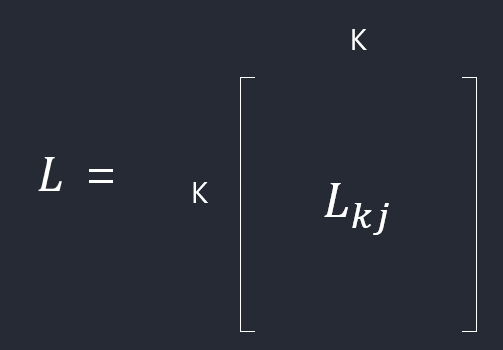
행은 실제 클래스, 열은 분류한 예측값이다.

데이터에 대한 모든 정보는 확률분포로 표현되고 있음을 기억해야 한다. 우리가 관찰할 수 있는 샘플은 확률 분포를 통해서 생성된 것이라고 간주한다.

따라서 손실행렬 \(L\)이 주어졌을 때, 다음과 같은 기대손실을 최소화 하는 것을 목표로 할 수 있다.

\[\mathbb E[L] = \sum_{k}\sum_{j}\int_{\mathcal{R_{i}}}\ L_{kj}p(\mathbf x,C_{k})d\mathbf x\]

기대손실 최소화

\(\mathbb E[L] = \sum_{k}\sum_{j}\int_{\mathcal{R_{i}}}\ L_{kj}p(\mathbf x,C_{k})d\mathbf x\)

\(\hat C(\mathbf x)\)를 \(\mathbf x\)가 주어졌을 때 예측값 \((1,...,K 중 하나의 값)\)을 돌려주는 함수

\[\mathbf x \in \mathcal{R_{i}} \Leftrightarrow \hat C(\mathbf x) = j\]

따라서 위의 \(\mathbb E[L]\) 식을 아래와 같이 표현할 수 있다.

• 위의 기대손실식에서는 \(L_{kj}\) 대신에 \(\hat C(\mathbf x)\)로 바꾸고
• 곱셈법칙을 이용해, 결합확률(\(p(\mathbf x, C_{k})\))을 조건부확률(\(p(C_{k}\mid \mathbf x)\))과 marginal prob(\(p(\mathbf x)\))로 바꿔주었다.

\[\begin{align} \int_{x}\sum_{k=1}^{K}L_{k\hat C(\mathbf x)}p(\mathbf x, C_{k})d\mathbf x \\\\ = \int_{x}\left( \sum_{k=1}^{K}L_{k\hat C(\mathbf x)}p(C_{k}\mid \mathbf x) \right)p(\mathbf x)d\mathbf x \\\\ \end{align}\]

이렇게 표현된 \(\mathbb E[L]\)는 \(\hat C(\mathbf x)\)의 범함수이고 이 범함수를 최소화시키는 함수 \(\hat C(\mathbf x)\)를 찾으면 된다.

수많은 덧셈을 최소화 시킨다고 생각해보면,
\(p(\mathbf x)\) > 0 이기 때문에
각각의 x에 대해서 \(\sum_{k=1}^{K}L_{k\hat C(\mathbf x)}p(C_{k}\mid \mathbf x)\) 이 부분만 최소화 시키게 되면
전체의 합이 최소화 될 것이다.

범함수: 흔히 함수를 상상할 때 숫자가 입력되었을 때 숫자를 출력시키는 가상의 상자라 생각한다. 이와 비슷하게 범함수를 어떤 상자로 상상한다면, 숫자 대신 함수가 입력되고 그에 대한 결과로 숫자가 출력되는 상자라고 할 수 있다.

• 숫자 -> 함수 f -> 숫자
• 함수 -> 범함수 f -> 숫자
• 함수의 함수라고 생각할 수 있다.
• 즉, \(\mathbb E[L]\)은 \(\hat C(\mathbf x)\)에 따라 값이 변하기 때문.

\[\hat C(\mathbf x) = \arg\min_{j}\sum_{k=1}^{K}\ L_{kj}p(C_{k}\mid\mathbf x)\]

: 가능한 \(j\)를 모두 시도를 했을 때 \(\sum_{k=1}^{K}\ L_{kj}p(C_{k}\mid\mathbf x)\)이 최소가 되는 j

만약에 손실행렬이 0-1 loss인 경우 (주대각선 원소들은 0 나머지는 1)

이 경우에 \(L_{kj}=1\), \(L_{jj}=0\) 이라는 사실을 활용해서,

\[\hat C(\mathbf x) = \arg\min_{j}\sum_{k=1}^{K}\ L_{kj}p(C_{k}\mid\mathbf x)\] \[= \sum_{k=1}^{K}\ p(C_{k}\mid\mathbf x) - p(C_{j}\mid \mathbf x)\] \[= 1 - p(C_{j}\mid \mathbf x)\]

따라서 \(1 - p(C_{j}\mid \mathbf x)\) 이 값을 최소화하는 것은 결국 \(p(C_{j}\mid \mathbf x)\) 이 값을 최대화 하는 것이다.

결론:

\[\begin{align} \hat C(\mathbf x) &= \arg\min_{j} 1 - p(C_{j}\mid\mathbf x) \\\\ &= \arg\max_{j} p(C_{j}\mid\mathbf x) \end{align}\]

• 위 식에서 \(= \sum_{k=1}^{K}\ p(C_{k}\mid\mathbf x) - p(C_{j}\mid \mathbf x)\) 이 부분이 잘 이해가 안된다. 대각이 0인건 알겠으나 어떻게 이렇게 변환되는지 모르겠다.

예제: 의료진단

\(C_{k} \in \{1,2\} \Leftrightarrow \{sick, healthy\}\)

\[L = \begin{bmatrix}0 & 100\\1 & 0\end{bmatrix}\]

L[1,1] = 0: sick & diagnosed as sick
L[1,2] = 100: sick & diagnosed as healthy

이 경우 기대손실(expected loss):

\[\begin{align} \mathbb E[L] &= \int_{\mathcal{R_{2}}}L_{1,2}p(\mathbf x, C_{1})d\mathbf x + \int_{\mathcal{R_{1}}}L_{2,1}p(\mathbf x, C_{2})d\mathbf x \\\\ &= \int_{\mathcal{R_{2}}}100\times p(\mathbf x, C_{1})d\mathbf x + \int_{\mathcal{R_{1}}}p(\mathbf x, C_{2})d\mathbf x \\\\ \end{align}\]

행 = Groundtruth
열 = Prediction(Diagnosis)

\(\int_{\mathcal{R_{2}}}L_{1,2}p(\mathbf x, C_{1})d\mathbf x\): predicted as healthy(\(\mathcal{R_{2}}\)), but groundtruth is sick(\(C_{1}\))
since \(L_{1,2}\) = 100, \(\ \int_{\mathcal{R_{2}}}L_{1,2}p(\mathbf x, C_{1})d\mathbf x = \int_{\mathcal{R_{2}}}100\times\ p(\mathbf x, C_{1})d\mathbf x\).

from this j = 1:
\(\hat C(\mathbf x) = \arg\min_{j}\sum_{k=1}^{K}\ L_{kj}p(C_{k}\mid\mathbf x)\)

\[L_{11} = 0, L_{21} = 1\] \[\begin{align} \sum_{k=1}^{K}\ L_{k,1}p(C_{k}\mid\mathbf x) & = L_{11}p(C_{1}\mid \mathbf x) + L_{21}p(C_{2}\mid \mathbf x)\\ &= p(C_{2}\mid \mathbf x) \\\\ \end{align}\]

j = 2:

\[\begin{align} \sum_{k=1}^{K}\ L_{k,2}p(C_{k}\mid\mathbf x) & = L_{12}p(C_{1}\mid \mathbf x) + L_{22}p(C_{2}\mid \mathbf x)\\ &= 100\times\ p(C_{1}\mid \mathbf x) \\\\ \end{align}\]

thus:
\(p(C_{2}\mid \mathbf x), 100\times\ p(C_{1}\mid \mathbf x)\)

건강하다(\(C_{2}\))고 판단하기 위한 조건은:
\(p(C_{2}\mid \mathbf x)> 100\times\ p(C_{1}\mid \mathbf x)\)
sick의 확률보다 100크게 나와야 한다.

안전하게 진단을 하기 위해서(오진단의 리스크를 줄이기 위해), 손실행렬을 모델안에 포함시켜서 결정을 내리는 것이 좋을 것이다.

Regression

목표값 \(t \in \mathcal{R}\)

손실함수: \(L(t,y(\mathbf x)) = \{y(\mathbf x)-t\}^{2}\)

손실값의 기댓값인 \(E[L]\)를 최소화시키는 함수 \(y(\mathbf x)\)를 구하는 것이 목표.

\[\begin{align} F[y] = E[L] &= \int_{\mathcal{R}}\int_{\mathcal{X}}\{ y(\mathbf x) - t \}^{2}p(\mathbf x, t)d\mathbf x dt \\ &= \int_{\mathcal{X}}\left( \int_{\mathcal{R}}\{ y(\mathbf x) - t \}^{2}p(\mathbf x, t)dt \right)d\mathbf x \\ &= \int_{\mathcal{X}}\left( \int_{\mathcal{R}}\{ y(\mathbf x) - t \}^{2}p(t\mid \mathbf x)dt \right)p(\mathbf x)d\mathbf x \\ \end{align}\]

결론:
\(\mathbf x\)를 위한 최적의 예측값은 \(y(\mathbf x) = \mathbb E_{t}[t\mid x]\)임을 보일 것이다.

\(\mathbb E_{t}[t\mid x]\): x가 주어졌을 때 t의 기댓값.

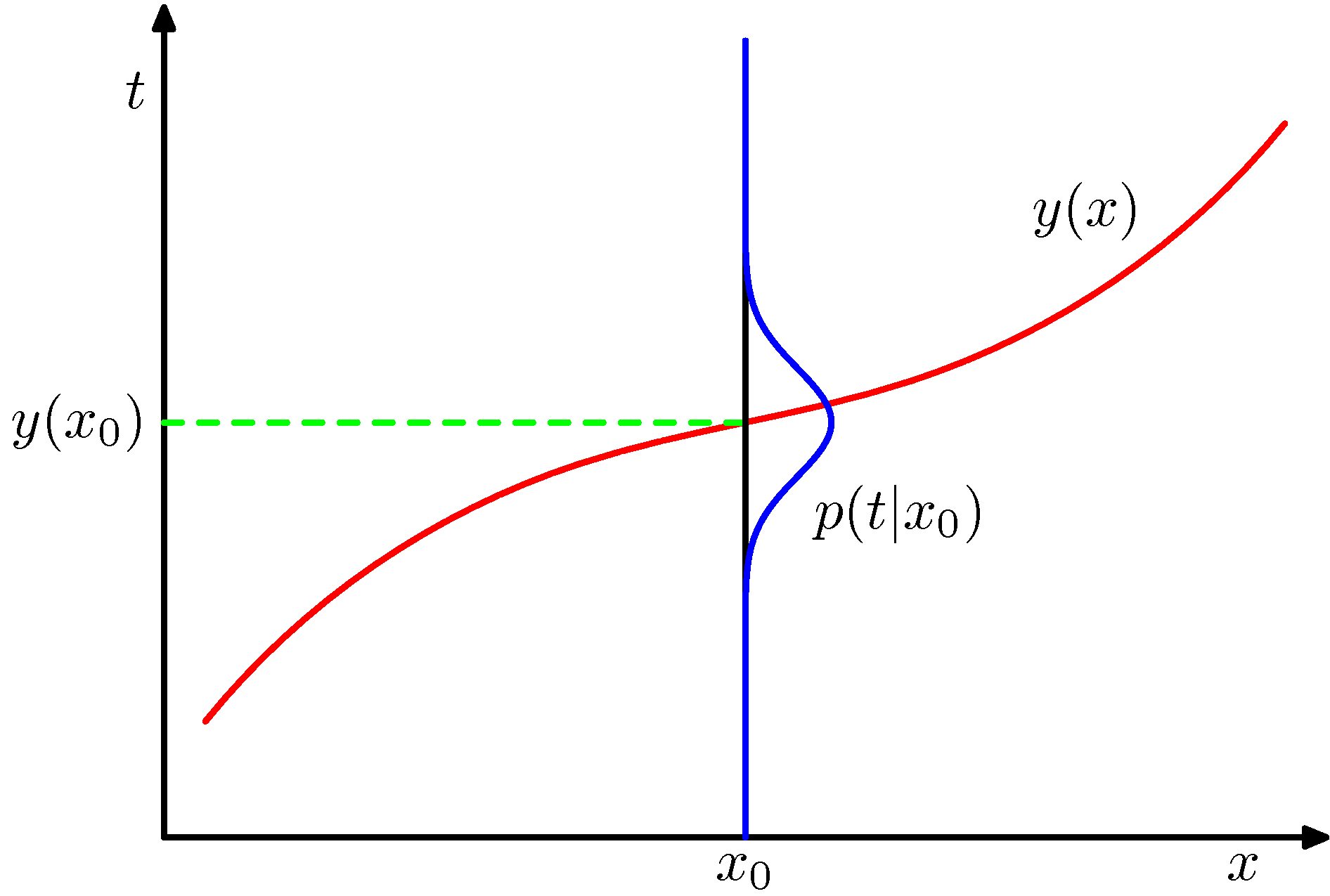
위 그림에서 우리가 알고 있는 것은 \(x_{0}\)가 주어졌을 때 t의 조건부확률 \(p(t\mid x_{0})\) 이고, 이것의 기댓값은 \(y(x_{0})\)이다.

Methods for Decision Problems

Classification

확률모델에 의존하는 경우

• 생성모델(generative model): 먼저 각 클래스 \(C_{k}\)에 대해 분포 \(p(\mathbf x\mid C_{k})\)와 사전확률 \(p(C_{k})\)를 구한 다음 베이즈 정리를 사용해서 사후확률 \(p(C_{k}\mid \mathbf x)\)를 구한다.

\[p(C_{k}\mid \mathbf x) = \frac{p(\mathbf x\mid C_{k})p(C_{k})}{p(\mathbf x)}\]

\(p(\mathbf x)\)는 다음과 같이 구할 수 있다.

\[p(\mathbf x) = \sum_{k}p(\mathbf x\mid C_{k})p(C_{k})\]

사후확률이 주어졌기 때문에 분류를 위한 결정은 쉽게 이루어질 수 있다. 결합분포에서 데이터를 샘플링해서 ‘생성’할 수 있으므로 이런 방식을 생성모델이라고 부른다.

• 식별모델(discriminative model): 모든 분포를 다 계산하지 않고 오직 사후확률 \(p(C_{k}\mid \mathbf x)\)를 구한다. 위와 동일하게 결정이론을 적용할 수 있다.

판별함수에 의존하는 경우

확률모델에 의존하지 않는 모델

• 판별함수(discriminant function): 입력 \(\mathbf x\)을 클래스로 할당하는 판별함수(discriminant function)을 찾는다. 확률값은 계산하지 않는다.

Regression

• 결합분포\(p(\mathbf x, t)\)를 구하는 추론(inference)문제를 먼저 푼 다음 조건부확률분포 \(p(t\mid \mathbf x)\)를 구한다. 그리고 주변화(marginalize)를 통해 \(\mathbb E_{t}[t\mid x]\)를 구한다.
• 조건부확률분포 \(p(t\mid \mathbf x)\)를 구하는 추론문제를 푼 다음 주변화(marginalize)를 통해 \(\mathbb E_{t}[t\mid x]\)를 구한다.
• \(y(\mathbf x)\)를 직접적으로 구한다.

Optional

Euler-Lagrange Equation

손실함수의 분해

Appendix

MathJax

\(\mathbb E\):

$$\mathbb E$$

\(\mathcal{R}\):

$$\mathcal{R}$$

\(\arg\min_{j}\):

$$\arg\min_{j}$$

matrix with bracket: \(L = \begin{bmatrix}a & b\\c & d\end{bmatrix}\)

$$L = \begin{bmatrix}a & b\\c & d\end{bmatrix}$$  

matrix with curly braces:
\(\begin{Bmatrix}aaa & b\cr c & ddd \end{Bmatrix}\)

$$\begin{Bmatrix}aaa & b\cr c   & ddd \end{Bmatrix}$$

가변 괄호 with escape curly brackets
\(\left\{-\frac{1}{2\sigma^{2}} \sum_{n=1}^{N}(x_{n}-\mu)^{2} \right\}\):

$$\left\{-\frac{1}{2\sigma^{2}} \sum_{n=1}^{N}(x_{n}-\mu)^{2} \right\}$$ 

References

Drawing Graph with PPT: https://www.youtube.com/watch?v=MQEBu9NnCuI
Decision Theory: http://norman3.github.io/prml/docs/chapter01/5.html
Pattern Recognition and Machine Learning: https://tensorflowkorea.files.wordpress.com/2018/11/bishop-pattern-recognition-and-machine-learning-2006.pdf