Heap Sort Implementation

코드 구현 원칙

1. 수도코드보고 구현
2. 실패시, 코드보고 코멘트 달고 작성해보기
3. 재귀로 구현 완성
4. iterative version 구현하기

Pseudo Code

• siftdown 구현
  • left child, right child
  • largest
  • swap
  • recursion
• heapify 구현
  • 전체 노드가 아닌 len//2 -1 의 index부터 시작해서 sort
• heapsort 구현
  • heapify 함수로 max heap 구조를 만든 후 root와 end 노드를 swap하고 siftdown 수행
    • swap, siftdown 수행후 end를 하나씩 줄여나간다.

재귀호출 구현

def heapsort(a):
    def siftdown(a, i, size):
        l = 2*i + 1
        r = 2*i + 2
        largest = i
        if l <= size-1 and a[l] > a[i]:
            largest = l
        if r <= size-1 and a[r] > a[largest]: # 자식노드 2개중 큰 것을 largest 변수에 넣어야 하기 때문에, r에서는 largest와 r을 비교
            largest = r
        if largest != i: # largest가 i와 다르다면, 즉, largest가 변경되었다면, swap을 해주고 siftdown
            # SWAP
            a[i], a[largest] = a[largest], a[i]
            siftdown(a, largest, size)

    def heapify(a, size):
        p = (size//2)-1 
        while p>=0:
            siftdown(a, p, size)
            p -= 1

    size = len(a)
    heapify(a, size) # MAX HEAP
    end = size-1
    while(end > 0):
        # root와 end를 swap 해준 후
        # root를 siftdown 해주면 정렬이 된다.
        # (swap된 노드(root에서 swap했으므로 현재는 end노드)는 siftdown에서 배제된 상태로 siftdown 진행된다.)
        # (root는 heapify된 후 이므로 최고 혹은 최소이기 때문에)
        a[0], a[end] = a[end], a[0]
        siftdown(a, 0, end) # root node 부터 siftdown을 진행
        end -= 1

Compare with Merge Sort

• summary:
  • Heap:
    • Unstable Sort
    • in-place: memory efficienty
  • Merge:
    • Stable Sort
    • \(O(n)\) extra space is required.

Stability in Sorting Algorithms

• The stability of a sorting algorithm is concerned with how the algorithm treats equal (or repeated) elements.
• Stable sorting algorithms preserve the relative order of equal elements, while unstable sorting algorithms don’t.

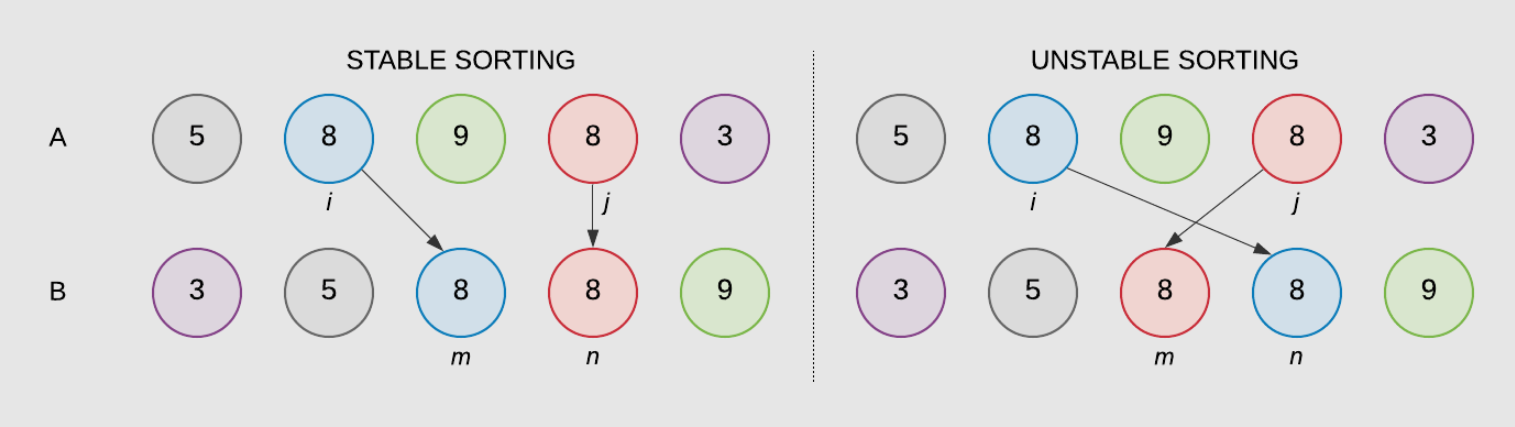
When Stability Matters

• Distinguishing Between Equal Elements
  • If the sort key is the (entire) element itself, equal elements are indistinguishable, such as integers or strings.
• Stable Sorting Is Important, Sometimes
  • We don’t always need stable sorting. Stability is not a concern if:
    • equal elements are indistinguishable, or
    • all the elements in the collection are distinct
• When equal elements are distinguishable, stability is imperative.
  • For instance, if the collection already has some order, then sorting on another key must preserve that order.

Stable and Unstable Sorting Algorithms

• Stable: Merge Sort, Timsort, Counting Sort, Insertion Sort, and Bubble Sort.
• Unstable: Quicksort, Heapsort and Selection Sort.

Iterative Heap Sort (TODO)

Appendix

Reference

힙 정렬 알고리즘 Heap Sort (part 1/2): https://youtu.be/WDm8a9GvQyU
Heap sort vs Merge sort || Comparision between heap sort and merge sort: https://youtu.be/5DYZEcSj2dE
Stability in Sortin Algorithm: https://www.baeldung.com/cs/stable-sorting-algorithms Stability in Sortin Algorithm: https://blog.naver.com/zephyehu/150013176075 Stability in Sortin Algorithm: https://www.geeksforgeeks.org/stability-in-sorting-algorithms/